2.9. Задачі на складання рівнянь

 

Розв’язування задач на складання рівнянь можна розбити на кілька етапів: вибір невідомих величин і їх позначення, запис вказаних співвідношень у вигляді рівнянь або систем рівнянь, розв’язання цих рівнянь або системи рівнянь з урахуванням області визначення (при цьому враховуються природні фізичні обмеження, які звичайно в тексті задач не наведено). Розглянемо розв’язання деяких типів задач.

  •  Задача на рух

    1. Відстань від пункту А до пункту Б залізницею дорівнює 105 км, а річкою – 150 км. Поїзд з пункту А виходить на 2 години пізніше від теплохода і прибуває до пункту Б на 15 хвилин раніше. Знайдіть швидкість (у кілометрах за годину) поїзда, якщо вона на 30 км/год більша за швидкість теплохода.

    Розв’язання

    Позначимо швидкість руху теплохода через х, тоді швидкість поїзда дорівнюватиме х+30. Час руху теплохода дорівнює , а поїзда – 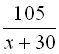. За умовою задачі, поїзд з пункту А виходить на 2 години пізніше від теплохода і прибуває до пункту Б на 15 хвилин раніше, то різниця у часі між теплоходом і поїздом становить 2 год 15 хв., або год. Отже, можна скласти рівняння 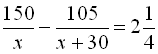. Розв’яжемо дане рівняння:

    .

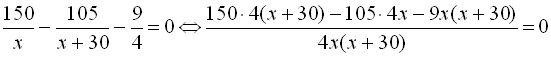    Областю допустимих значень даного рівняння є , звідси та , що і так не можливо згідно з умовою задачі. Тоді прирівняємо чисельник останнього рівняння до нуля

    . Коренями отриманого квадратного рівняння є , (не підходить, оскільки швидкість не може бути від’ємною). Отже, швидкість теплохода – 40 км/год. Тоді швидкість поїзда – 70 км/год.

    Відповідь: 70 км/год.

  •  Задача на спільну роботу

    2. Двом друкаркам було доручено деяке завдання. Друга друкарка почала працювати на 1 годину пізніше, ніж перша. Через 3 години після того, як перша друкарка почала роботу, обом їм залишилося виконати усієї роботи. Коли завдання було виконано, виявилося, що кожна друкарка зробила половину всієї роботи. За скільки годин кожна друкарка окремо може виконати всю роботу?

    Розв’язання

    Позначимо через x та y час (у годинах) виконання всієї роботи першою і другою друкаркою відповідно, тоді за 1 год. перша друкарка виконає , а друга – частину всієї роботи. За умовою задачі складемо перше рівняння: 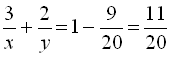. Половину всієї роботи перша друкарка виконала за год., а друга – за год. Оскільки друга друкарка працювала на 1 год. менше, ніж перша, маємо друге рівняння: 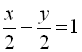. Далі складемо систему 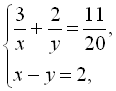і розв’яжемо її в системі Maple:

    > solve({3/x+2/y=11/20,x-y=2},{x,y});

    Умову задачі задовольняють лише значення

    Відповідь: 10 год., 8 год.

  •  Задача на концентрацію

    3. Маємо два сплави золота і срібла. У першому сплаві ці метали знаходяться у відношенні 1:2, а у другому – у відношенні 2:3. Скільки грамів кожного сплаву треба взяти, щоб дістати 19 г сплаву з відношенням золота і срібла 7:12?

    Розв’язання

    Позначимо за х масу першого сплаву, тоді маса другого сплаву дорівнює 19 – х. Оскільки у першому сплаві золото і срібло знаходяться у відношенні 1:2, то у цьому сплаві 1 частина золота та 2 частини срібла, тобто всього 3 частини. Отже, маса золота складає маси першого сплаву. Аналогічним чином знаходимо, що маса золота у другому сплаві складає маси всього сплаву. 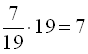У новому сплаві маса золота складає від 19 грамів, тобто грам. Складемо рівняння 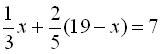, звідки

    Відповідь: 9 г і 10 г.

  •  Задача на знаходження числа

    4. Знайти двозначне число, яке при діленні на добуток його цифр дає частку , а різниця між ним та числом з переставленими цифрами дорівнює 18.

    Розв’язання

         Позначимо через x та y першу і другу цифри, тоді невідоме число матиме вигляд , а число з переставленими цифрами . Запишемо систему рівнянь 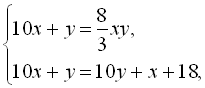звідки знаходимо: Отже, – шукане число.

    Відповідь: 64.

    		•