2.7. Симетричні рівняння
Раціональне рівняння третього степеня називається симетричним, якщо
воно має вигляд: ![]()
![]() .
.
Скористаємось системою Maple для розкладання лівої частини даного рівняння на множники:
> factor(a*x^3+b*x^2+b*x+a);
![]()
Дійсно, якщо згрупувати перший з останнім, а другий з третім доданки даного рівняння, отримаємо
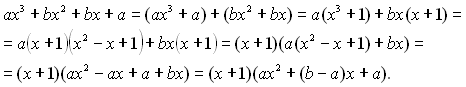
Звідси дістаємо ![]()
![]()
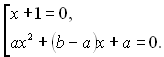
Розв’язок отриманої сукупності легко знаходиться, оскільки ця сукупність містить лінійне і квадратне рівняння.
Приклад 23. Розв’язати рівняння: ![]()
Розв’язання
![]()
![]()
Звідси ![]()
![]()
![]()
![]()
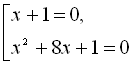
![]()
![]()
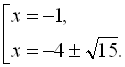
Відповідь: {-1; ![]() }.
}.
Рівняння виду ![]()
![]() називається зворотним, якщо виконується умова
називається зворотним, якщо виконується умова 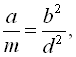
![]() Оскільки
Оскільки ![]() не є розв’язком зворотного рівняння, то можна поділити обидві частини рівняння
на
не є розв’язком зворотного рівняння, то можна поділити обидві частини рівняння
на ![]() і після заміни змінних одержати квадратне рівняння.
і після заміни змінних одержати квадратне рівняння.
Детальніше розглянемо на прикладі.
Приклад 24. Розв’язати рівняння: ![]()
Розв’язання
Поділивши початкове рівняння на ![]() ,
, ![]() ,
дістаємо
,
дістаємо
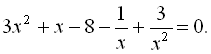 Згрупувавши доданки, маємо
Згрупувавши доданки, маємо
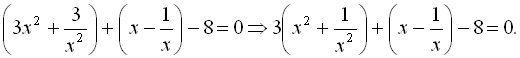
Поклавши 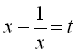 ,
маємо
,
маємо 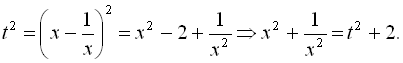
Таким чином, приходимо до рівняння
![]()
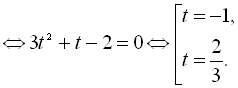
Повертаючись до заміни, маємо
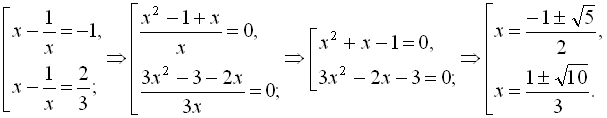
Відповідь: 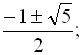
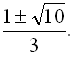
2.8. Системи рівнянь
Кілька рівнянь з двома (або більше) змінними утворюють систему рівнянь, якщо ставиться задача знайти множину спільних розв’язків цих рівнянь. Систему двох рівнянь з двома змінними позначають фігурними дужками і, зазвичай, записують у вигляді
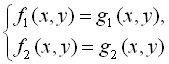 .
.
Розв’язати систему рівнянь – значить знайти всі її розв’язки або довести, що розв’язків немає. Система називається сумісною, якщо вона має хоча б один розв’язок, і несумісною, якщо вона не має жодного розв’язку.
Система рівнянь називається визначеною, якщо вона має скінченне число розв’язків, і невизначеною, якщо вона має нескінченну множину розв’язків.
Дві системи називаються рівносильними, якщо вони мають ту саму множину розв’язків.
Симетричною системою рівнянь називається система, всі рівняння якої симетричні.
Вираз ![]() називається симетричним, якщо при заміні х на у,
у на х він не змінюється.
називається симетричним, якщо при заміні х на у,
у на х він не змінюється.
Приклади симетричних виразів:
![]() ;
; ![]() ;
; ![]() ;
;
![]() =
=![]()
![]()
Вирази ![]() і
і ![]() називаються основними симетричними многочленами з двома
змінними. Усі симетричні вирази з двома змінними виражаються через основні
симетричні многочлени, наприклад:
називаються основними симетричними многочленами з двома
змінними. Усі симетричні вирази з двома змінними виражаються через основні
симетричні многочлени, наприклад:
![]() ;
; ![]() ;
;
![]() За допомогою системи Maple подібне перетворення можна здійснити таким чином
За допомогою системи Maple подібне перетворення можна здійснити таким чином
> simplify(x^3+y^3,{x+y=u,x*y=v});
![]()
Система двох рівнянь з двома змінними називається однорідною, якщо ліві частини її рівнянь, що містять змінні, є однорідними многочленами степеня п від двох змінних. Таким чином, однорідна система з двома змінними має вигляд
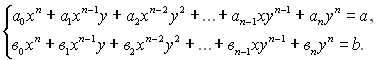
Властивості систем рівнянь:
1. Будь-яке рівняння системи можна замінити сумою рівнянь систем:
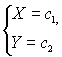
![]()
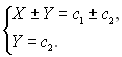
2. Будь-яке рівняння системи можна замінити добутком рівнянь систем: 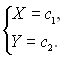
![]()
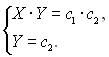
Основні методи розв'язування систем рівнянь:
1) Метод підстановки. Спочатку за допомогою якого-небудь рівняння системи виражають одну змінну через іншу. Отриманий вираз підставляють в інше рівняння системи, в результаті чого приходять до рівняння з одною змінною, потім розв’язують це рівняння і знаходять відповідне значення іншої змінної.
2) Метод алгебраїчного додавання. При розв’язуванні системи цим методом переходять від даної системи до рівносильної їй системи, в якій одне з рівнянь містить лише одну змінну. При цьому звичайно множать одне або обидва рівняння на числові множники таким чином, щоб коефіцієнти при х або у були однаковими, але з протилежними знаками.
3) Метод введення нових змінних. Цей метод розв’язування систем розглянемо на прикладі 20.
Розв’язувати симетричну систему можна, наприклад, за допомогою заміни змінних, де новими змінними є основні симетричні многочлени.
Однорідні системи розв’язуються за допомогою застосування методів алгебраїчного додавання і введення нових змінних.
Ще одним способом розв’язування рівнянь є
графічний. Нехай, наприклад, потрібно розв’язати систему 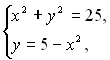 обидва рівняння якої є рівняннями другого степеня. Графіком рівняння
обидва рівняння якої є рівняннями другого степеня. Графіком рівняння ![]() є коло, а графіком рівняння
є коло, а графіком рівняння ![]() – парабола. Ці графіки мають три спільні точки:
– парабола. Ці графіки мають три спільні точки: ![]() ,
, ![]() ,
, ![]() .
Легко перевірити, що координати кожної з цих
.
Легко перевірити, що координати кожної з цих 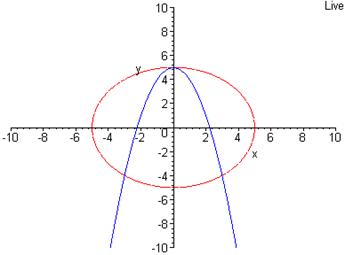 точок
є розв’язком як першого, так і другого рівнянь системи. Тобто, система має 3
розв’язки. Отже, щоб розв’язати систему рівнянь із двома змінними графічним
способом, потрібно побудувати графіки рівнянь системи в одній системі координат
і знайти координати спільних точок цих графіків.
точок
є розв’язком як першого, так і другого рівнянь системи. Тобто, система має 3
розв’язки. Отже, щоб розв’язати систему рівнянь із двома змінними графічним
способом, потрібно побудувати графіки рівнянь системи в одній системі координат
і знайти координати спільних точок цих графіків.
Але цей спосіб не є основним способом розв’язування рівнянь, тому що він не завжди дає точні результати.
Приклади систем рівнянь та їх розв’язування:
Приклад 25. Розв’язати систему рівнянь 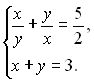
Розв’язання
1-й спосіб розв’язування:
Розв’яжемо дану систему рівнянь методом підстановки, для цього з другого рівняння системи визначимо у і підставимо його у перше рівняння:
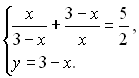
Розв’яжемо перше рівняння отриманої системи: ![]()
Перенесемо ![]() у ліву частину і зведемо вираз до спільного знаменника:
у ліву частину і зведемо вираз до спільного знаменника:
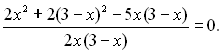
За умови, що знаменник ![]() маємо:
маємо:
![]() ,
тоді, розкривши дужки,
,
тоді, розкривши дужки,
![]()
![]()
![]() .
.
Зведемо подібні: ![]()
![]()
![]()
За теоремою Вієта: ![]()
Отже, 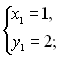 або
або 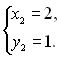
2-й спосіб розв’язування:
У першому рівнянні системи 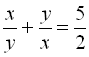 зробимо заміну
зробимо заміну ![]() ,
тоді
,
тоді
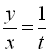 .
Одержуємо рівняння
.
Одержуємо рівняння 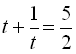
![]()
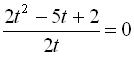
![]()
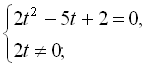
![]()
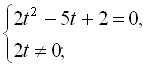
![]()
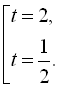 Повернемось до заміни:
Повернемось до заміни: 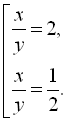
Враховуючи друге рівняння початкової системи, отримаємо сукупність двох систем:
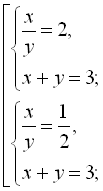
![]()
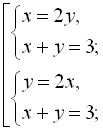
![]()
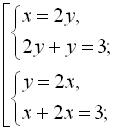
![]()
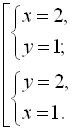
Відповідь: (1; 2), (2; 1).
Як і рівняння, системи алгебраїчних рівнянь розв’язуються в системі Maple за допомогою функції solve. Для систем структура даної функції виглядає так:
solve({рівняння1, рівняння 2, … },{змінна1, змінна2, …});
Покажемо на попередньому прикладі:
> solve({x/y+y/x=5/2,x+y=3},{x,y});
![]()
Дана форма дозволяє розв’язати системи рівнянь відносно змінних, які задані другим параметром. Звернемо увагу на те, що система рівнянь і її невідомі змінні задаються у вигляді множин. Результатом в даному випадку є також множина значень невідомих у вигляді рівнянь, тоді як у випадку задання одного рівняння є виразом (у випадку одного кореня рівняння) або послідовністю виразів (у випадку декількох коренів).
Приклад 26. Розв’язати систему рівнянь 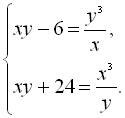
Розв’язання
Розв’яжемо дану систему методом алгебраїчного додавання, для цього перемножимо рівняння системи і одержимо:
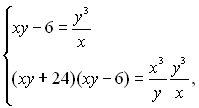 (1)
(1)
Друге рівняння отриманої системи шляхом нескладних перетворень зводиться до
рівняння ![]() – наслідку другого рівняння системи (1). Тоді система
– наслідку другого рівняння системи (1). Тоді система 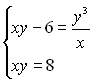 (2) буде наслідком системи (1).
(2) буде наслідком системи (1).
Віднімемо тепер перше рівняння системи (2) від другого. Отримаємо систему 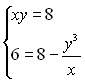 або
або 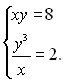 (3)
(3)
Система (3) – наслідок системи (2).
Перемножимо рівняння системи (3) і отримаємо систему
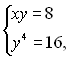 (4)
(4)
яка буде наслідком системи (3). З другого рівняння системи (4) знаходимо ![]() ,
а з першого рівняння, відповідно,
,
а з першого рівняння, відповідно, ![]()
Таким чином, система (4) має такі розв'язки:
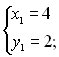 або
або 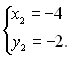
Відповідь: (4; 2), (-4; -2).
Приклад 27. Розв'язати систему рівнянь 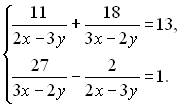
Розв'язання
Розв’яжемо дану систему методом заміни змінної:
Позначимо 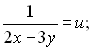
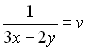 .
.
Зробивши заміну, дістанемо нову систему:
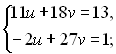 або
або 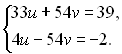
![]()
![]()
![]() ;
; ![]()
![]()
![]() .
.
Повернемось до попередніх змінних:
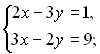
![]()
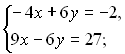
![]()
![]()
Відповідь: (5; 3).


