2.6. Розв’язування раціональних і дробово-раціональних рівнянь методом введення нової змінної
Метод введення нової змінної був використаний раніше при розв’язуванні тричленних рівнянь, однак цей метод з успіхом застосовується і при розв’язуванні багатьох інших рівнянь, де можлива і корисна заміна змінної. Для закріплення цього методу розглянемо кілька прикладів.
Приклад 18. Розв’язати рівняння ![]()
Розв’язання
Поклавши ![]() ,
дістанемо рівняння
,
дістанемо рівняння ![]() ,
звідки знаходимо
,
звідки знаходимо ![]() Тепер задача звелася до розв’язування сукупності рівнянь
Тепер задача звелася до розв’язування сукупності рівнянь 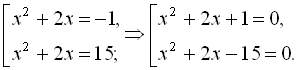 Перше рівняння сукупності має кратний корінь
Перше рівняння сукупності має кратний корінь ![]() друге рівняння має корені
друге рівняння має корені ![]() .
.
Відповідь: ![]()
Приклад 19. Розв’язати рівняння 
Розв'язання
 .,
.,
Поклавши ![]() ,
дістанемо рівняння
,
дістанемо рівняння 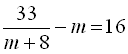 .
Переносимо всі доданки рівняння в одну частину і зводимо до спільного
знаменника:
.
Переносимо всі доданки рівняння в одну частину і зводимо до спільного
знаменника:

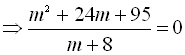
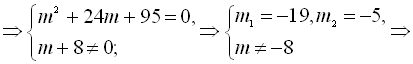
![]()
Узявши ![]() .
Оскільки диск-римінант цього рівняння
.
Оскільки диск-римінант цього рівняння ![]() ,
то воно дійсних коренів не має.
,
то воно дійсних коренів не має.
Узявши ![]() .
.
Зробимо перевірку в системі Maple:
> subs(x=1,33/(x^2-6*x+8)-x^2+6*x=16);
![]()
> subs(x=5,33/(x^2-6*x+8)-x^2+6*x=16);
![]()
Отже, обидва корені є розв’язком нашого рівняння.
Відповідь: {1; 5}.
У дробово-раціональних рівняннях часто потрібно знаходити область допустимих значень (коротко ОДЗ). Її, як правило, знаходять на початку розв’язання прикладу. У попередньому прикладі натомість знаходження області допустимих значень ми застосували перевірку знайдених коренів.
Приклад 20. Розв’язати рівняння 
Розв'язання
Покладемо 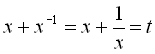 .
До речі, ОДЗ:
.
До речі, ОДЗ: ![]() .
Тоді
.
Тоді
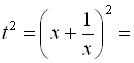

![]() .
.
Початкове рівняння записується у вигляді 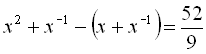
або 
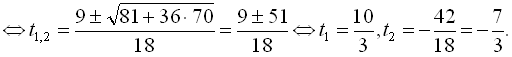
Узявши 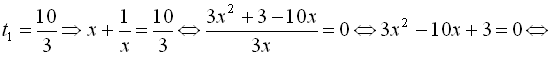
![]()
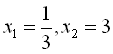 .
.
Узявши 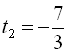 ,
дістаємо
,
дістаємо 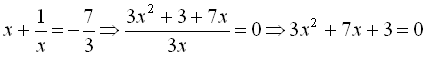

Відповідь: {
![]() 3}.
3}.
Приклад 21. Розв’язати рівняння 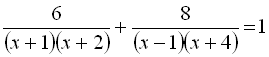 .
.
Розв'язання
Знайдемо ОДЗ: ![]() та
та ![]() або
або ![]() .
.
Доречним буде сказати, що в системі Maple знак ![]() вводиться у вигляді <>, а пуста множина позначається як {}.
вводиться у вигляді <>, а пуста множина позначається як {}.
Розкриємо дужки у знаменниках дробів: 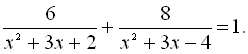 Як бачимо, можна зробити заміну
Як бачимо, можна зробити заміну ![]() ,
тоді утворене рівняння буде мати вигляд:
,
тоді утворене рівняння буде мати вигляд: 
![]()
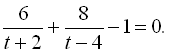
За допомогою команди normal зведемо ліву частину утвореного рівняння до спільного знаменника:
> normal(6/(t+2)+8/(t-4)-1=0);
![]()
Тепер знайдемо корені цього рівняння, хоча їх можна було б знайти і не виконуючи попередньої дії:
> solve(6/(t+2)+8/(t-4)-1=0);
![]()
Тобто, ![]() або
або ![]() .
Повертаємось до заміни:
.
Повертаємось до заміни: ![]() або
або ![]() .
.
> solve(x^2+3*x=0);
![]()
> solve(x^2+3*x=16);
![]()
Отже, маємо такі розв’язки: 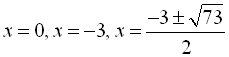 .
.
Всі отримані числа задовольняють ОДЗ, тому є коренями нашого рівняння.
Приклад 22. Розв’язати рівняння ![]()
Розв'язання
Рівняння виду ![]()
![]() розв’язується за допомогою заміни
розв’язується за допомогою заміни  (с – середнє арифметичне чисел а і b). Для рівняння
(с – середнє арифметичне чисел а і b). Для рівняння ![]()
 робимо заміну
робимо заміну ![]()
![]()
![]() початкове рівняння записується у вигляді
початкове рівняння записується у вигляді ![]() .
Застосовуючи трикутник Паскаля, отримуємо
.
Застосовуючи трикутник Паскаля, отримуємо
![]()
![]()
![]() .
Розв’язуючи це біквадратне рівняння, дістаємо
.
Розв’язуючи це біквадратне рівняння, дістаємо ![]()
![]() .
.
Узявши ![]() .
.
Узявши ![]() .
.
Відповідь: ![]() .
.


