2.5. Цілі раціональні рівняння вищих степенів
Рівняння виду ![]()
![]()
![]() є алгебраїчним рівнянням степеня п. Якщо
є алгебраїчним рівнянням степеня п. Якщо ![]() , то рівняння називається рівнянням вищого степеня. Таке рівняння має не більше п дійсних коренів.
, то рівняння називається рівнянням вищого степеня. Таке рівняння має не більше п дійсних коренів.
Рівняння ![]() називається незведеним цілим раціональним рівнянням
називається незведеним цілим раціональним рівнянням ![]() .
.
Рівняння ![]() називається зведеним цілим раціональним рівнянням.
називається зведеним цілим раціональним рівнянням.
Позначимо ![]() . Для рівняння
. Для рівняння ![]() справедлива теорема Безу: многочлен
справедлива теорема Безу: многочлен ![]() ділиться без остачі на двочлен
ділиться без остачі на двочлен ![]()
![]() в тому і тільки в тому випадку, коли
в тому і тільки в тому випадку, коли ![]() – корінь
– корінь
многочлена ![]() .
.
Якщо нескоротний дріб ![]() є коренем незведеного цілого раціонального рівняння з цілими коефіцієнтами
є коренем незведеного цілого раціонального рівняння з цілими коефіцієнтами
![]() , то
, то ![]() є дільником старшого коефіцієнта
є дільником старшого коефіцієнта ![]() , а
, а ![]() є дільником вільного члена
є дільником вільного члена ![]() .
.
Розв’язання рівнянь вищих степенів, що мають хоча б один цілий корінь, виконують в такому порядку:
1) знаходять множину дільників вільного члена ![]() ;
;
2) за теоремою Безу перевіряють, які з цих дільників є коренями рівняння ![]() ;
;
3) діленням у стовпчик знаходять частку від ділення ![]() на
на ![]() , де
, де ![]() – корінь рівняння
– корінь рівняння ![]() ;
;
4) записують частку ![]() як багаточлен степеня
як багаточлен степеня ![]() :
:  , де
, де ![]() – многочлен степеня
– многочлен степеня ![]() :
:
5) визначають, якщо це можливо, корені многочлена ![]() , які є також коренями початкового рівняння.
, які є також коренями початкового рівняння.
Приклад 15. Розв’язати рівняння: ![]() .
.
Розв’язання
Тут ![]() , тому, якщо дане рівняння має раціональні корені, то їх слід шукати серед дільників числа 6: ±1, ±2, ±3, ±6. Перевіркою дізнаємось, що
, тому, якщо дане рівняння має раціональні корені, то їх слід шукати серед дільників числа 6: ±1, ±2, ±3, ±6. Перевіркою дізнаємось, що ![]() є коренем початкового рівняння. За теоремою Безу початковий многочлен ділиться без остачі на
є коренем початкового рівняння. За теоремою Безу початковий многочлен ділиться без остачі на ![]() . Поділивши їх, отримаємо многочлен
. Поділивши їх, отримаємо многочлен ![]() .
.
Таким чином, ![]() . Тоді початкове рівняння набуває вигляду
. Тоді початкове рівняння набуває вигляду ![]() . Це рівняння рівносильне сукупності рівнянь:
. Це рівняння рівносильне сукупності рівнянь:  . Розв’язок першого рівняння
. Розв’язок першого рівняння ![]() уже знайдений. Друге рівняння сукупності має корені
уже знайдений. Друге рівняння сукупності має корені ![]() і
і ![]() .
.
Приклад 16. Розв’язати рівняння: ![]() .
.
Розв’язання
![]()
![]() , тому раціональні корені рівняння шукаємо серед чисел ±1,
, тому раціональні корені рівняння шукаємо серед чисел ±1, ![]()
![]() . Перевіряючи ці числа шляхом підстановки у початкове рівняння, знаходимо корінь
. Перевіряючи ці числа шляхом підстановки у початкове рівняння, знаходимо корінь ![]() . Звідси, потрібно поділити початковий многочлен лівої частини рівняння на
. Звідси, потрібно поділити початковий многочлен лівої частини рівняння на 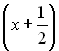 або, що те ж саме, але без дробів, на
або, що те ж саме, але без дробів, на  (тоді ми при діленні уникаємо дробових коефіцієнтів).
(тоді ми при діленні уникаємо дробових коефіцієнтів).
Скористаємось командою factor для розкладання многочлена на множники системи Maple. Відносно даної команди слід пам’ятати, що вона розкладає многочлен на множники над числовим полем, якому належать коефіцієнти многочлена. Це означає, що якщо всі коефіцієнти цілі, то і в отриманих множниках будуть лише цілі коефіцієнти. У даній команді можна вказати, над яким числовим полем слід здійснити розклад многочлена.
> factor(4*x^4+8*x^3+x^2-3*x-1=0);
![]()
Як бачимо, множник ![]() у другому степені, а це означає, що, використовуючи теорему Безу, нам потрібно ділити многочлен на множник
у другому степені, а це означає, що, використовуючи теорему Безу, нам потрібно ділити многочлен на множник  двічі.
двічі.
Ми задавали дане рівняння з цілими коефіцієнтами, тому вираз ![]() не розклався на множники, оскільки на раціональні множники він не розкладається. Розв’яжемо рівняння
не розклався на множники, оскільки на раціональні множники він не розкладається. Розв’яжемо рівняння ![]() на множині ірраціональних чисел:
на множині ірраціональних чисел:
> solve({x^2+x-1=0},{x});
![]()
Розв’язуючи початкове рівняння, отримаємо:
> solve({4*x^4+8*x^3+x^2-3*x-1=0},{x});
![]()
Відповідь: ![]()
Слід зазначити, що у випадку, коли ліва частина раціонального рівняння вищого степеня може бути розкладена на множники групуванням або яким-небудь іншим способом, розв’язок рівняння може бути отриманим більш простим шляхом.
Приклад 17. Розв’язати рівняння: ![]() .
.
Розв’язання
Розкладемо один із членів даного тричлена на доданки: ![]()
![]() або
або ![]() , тепер згрупуємо доданки зручним для нас способом, наприклад:
, тепер згрупуємо доданки зручним для нас способом, наприклад:
 або
або
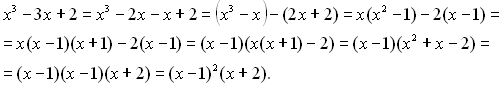
Отже, ![]() , тоді
, тоді 
Відповідь: {-2; 1}.
> x^3-3*x+2=0: solve(%,{x});
![]()


