2.3. Двочленні рівняння
Алгебраїчне рівняння називається двочленним рівнянням, якщо воно має вигляд ![]() .
.
Приклад 8. Розв’язати рівняння ![]() .
.
Розв’язання
![]()
![]()
![]() . Часто учні, розв’язуючи такі рівняння, знаходять лише один розв’язок рівняння
. Часто учні, розв’язуючи такі рівняння, знаходять лише один розв’язок рівняння ![]() .
.
Перевіримо за допомогою Maple
> with(RealDomain):
solve({x^4-625=0},{x});
![]()
Відповідь: ![]()
Команда with підключає пакет RealDomain, в результаті чого область комплексних чисел, в якій за замовчуванням працює система Maple, заміняється на область дійсних чисел. Це, зокрема, приводить до того, що команда solve повертає тільки дійсні корені рівняння.
Приклад 9. Розв’язати рівняння ![]()
Розв’язання
![]()
Відповідь: 3.
Або розкладемо ліву частину рівняння на множники:
> factor(x^3-27=0);
![]()
Прирівнявши перший множник до нуля, отримаємо корінь ![]() , а другий множник – це неповний квадрат суми, тому, прирівнявши його до нуля, дійсних коренів не отримаємо.
, а другий множник – це неповний квадрат суми, тому, прирівнявши його до нуля, дійсних коренів не отримаємо.
Приклад 10. Розв’язати рівняння ![]()
Розв’язання
![]() , а це неможливо, тому рівняння розв’язків не має.
, а це неможливо, тому рівняння розв’язків не має.
Відповідь:![]() .
.
Приклад 11. Розв’язати рівняння ![]()
Розв’язання
![]()
Відповідь: 0.
Цікаво звернути увагу на розв’язок цього ж рівняння в системі Maple:
> solve({x^12=0},{x});
![]()
> nops([%]);
![]()
Команда nops повертає кількість елементів списку.
2.4. Тричленні рівняння
Означення. Алгебраїчне рівняння виду ![]() називається тричленним, якщо
називається тричленним, якщо ![]()
![]()
![]()
![]() . При
. При ![]() тричленне рівняння називається біквадратним рівнянням. Заміною змінних
тричленне рівняння називається біквадратним рівнянням. Заміною змінних ![]() тричленне рівняння
тричленне рівняння ![]() перетворюється в квадратне
перетворюється в квадратне ![]() . Зокрема, для біквадратного рівняння
. Зокрема, для біквадратного рівняння ![]() заміна
заміна ![]() приводить його до квадратного рівняння
приводить його до квадратного рівняння ![]() .
.
Приклад 12. Розв’язати рівняння ![]() .
.
Розв’язання
Поклавши ![]() , дістаємо
, дістаємо ![]() . За теоремо Вієта
. За теоремо Вієта 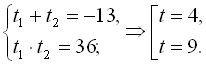
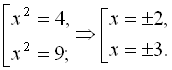
> solve({x^4-13*x^2+36=0},{x});
![]()
Відповідь: {±2; ±3}.
До речі, у системі Maple є можливість зробити перевірку на правильність розв’язання рівняння. Це робимо за допомогою команди subs(), наприклад, перевіримо правильність розв’язання прикладу № 5:
> subs(x=2,x^4-13*x^2+36);
![]()
> subs(x=3,x^4-13*x^2+36);
![]()
> subs(x=-2,x^4-13*x^2+36);
![]()
> subs(x=-3,x^4-13*x^2+36);
![]()
Зробивши перевірку, ми переконалися, що дані корені є розв’язками рівняння.
Система Maple має власну мову програмування надвисокого рівня. Дії, реалізація яких в традиційних мовах програмування займає десятки рядків, Maple дозволяє реалізувати записом в один рядок. Наприклад, в попередньому прикладі зовсім необов’язково записувати команду підстановки subs для кожного кореня окремо. Це можна зробити за допомогою команди створення послідовності seq:
> f:=x^4-13*x^2+36:
solve(f,{x});
seq(subs([%][k],f),k=1..nops([%]));
![]()
![]()
Приклад 13. Розв’язати рівняння ![]()
Розв’язання
Заміна ![]() , одержимо
, одержимо ![]() . Розкладемо ліву частину останнього рівняння на множники:
. Розкладемо ліву частину останнього рівняння на множники:
> factor(t^2-3*t+2=0);
![]()
> solve({t^2-3*t+2=0},{t});
![]()
Повернемось до заміни: 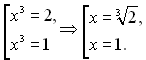
Відповідь: {1; ![]() }.
}.
Приклад 14. Розв’язати рівняння ![]()
(Заміна ![]() ).
).
Відповідь: {±1; ±2}.


