2.2. Квадратні рівняння

Рівняння виду називається квадратним рівнянням з однією змінною.

Якщо , то квадратне рівняння називається повним. Якщо , то квадратне рівняння називається зведеним, якщо – незведеним. Незведене квадратне рівняння завжди можна зробити зведеним, розділивши обидві частини його на перший коефіцієнт .

– зведене квадратне рівняння.

Корені квадратного рівняння знаходять за формулою , де називається дискримінантом квадратного рівняння.

Наведемо деякі перетворення, які можна здійснювати з рівняннями в Maple.

Якщо ми просто запишемо в командному рядку квадратне рівняння та натиснемо , то воно буде виведено на екран.

> a*x^2+b*x+c=0;

> whattype(%);

> f:=a*x^2+b*x+c=0;

> whattype(f);

При перевірці типу змінної, значенням якої є рівняння, за допомогою команди whattype() результатом є рівність, яка означає, що тип змінної, яка перевіряється, є рівнянням.

Знак (:=) означає присвоєння, тобто, що даному рівнянню присвоїли змінну f. Інколи рівнянню присвоюють одну або дві початкові букви англійської назви рівняння, тобто

> eq1:=x^4-3*x^2+2=0;

> eq1+(6*x^2-2=x);

Як бачимо, таке присвоєння є зручним в даному випадку, щоб в останньому рядку не набирати знову рівняння , а скористатися присвоєнням.

     Для розв’язування рівнянь і систем рівнянь, нерівностей і систем нерівностей існує одна із найбільш потужних та корисних команд solve. Ця команда прагне знайти замкнутий розв’язок в аналітичній формі. Її синтаксис, як і синтаксис інших команд Maple, достатньо простий і легко запам’ятовується:

solve(рівняння чи нерівність, змінна),

причому у випадку рівняння (нерівності) з однією змінною, змінну можна не вказувати.

Cкористаємось вищезгаданою функцією solve для отримання загального розв’язку квадратного рівняння:

> solve({a*x^2+b*x+c=0},{x});`Розв_кв_рівн`:=%:

Задамо коефіцієнтам квадратного рівняння конкретних значень. Наприклад, розв’яжемо рівняння . Тут же прослідкуємо відмінність в структурі функції solve:

> solve(2*x^2-5*x+2=0,x);

> solve({5*x^2-18*x+9=0},{x});

Оскільки ми зберегли загальний розв’язок квадратного рівняння у змінній `Розв_кв_рівн`, то частинні розв’язки для будь-яких значень змінних a, b, c (a ?0) можна отримати за допомогою команди subs:

> subs(a=5,b=-18,c=9,[`Розв_кв_рівн`]);

> simplify(%);

     Після спрощення дістали той самий результат.

Коли Maple не може знайти жодного розв’язку, то команда solve повертає пусту послідовність NULL. Це означає, що або розв’язок не існує, або системі не вдалося його знайти.

Якщо у квадратному рівнянні другий коефіцієнт b або вільний член с дорівнюють нулю, то таке рівняння називається неповним.

Розглянемо розв’язування рівняння , коли:

1) , звідки або , тоді , .

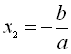Розглянемо його в системі Maple

> solve({a*x^2+b*x=0},{x});

Наприклад: . Для початку ліву частину даного рівняння потрібно розкласти на множники:

> factor(3*x^2-8*x=0);

,

а потім знаходимо корені даного рівняння

> solve({3*x^2-8*x=0},{x});

2)  , якщо ,

то рівняння не має дійсних коренів, лише якщо .

> solve({a*x^2+c=0},{x});

Варто звернути увагу на те, що система видала результат не в такому вигляді, як ми записали. Це тому, що запис, у якому в знаменнику міститься вираз з коренем, вважається неправильним. Наприклад, коли ліву частину рівняння спробувати розкласти на множники за допомогою системи Maple, то

> factor(3*x^2-11=0);

> solve(3*x^2-11=0);

А якщо за допомогою системи Maple спробувати розкласти на множники вираз

> factor(3*x^2+11=0);

то нічого не вийшло, оскільки вираз неможливо розкласти на дійсні множники, тому розв’язку дане рівняння не має.

3) 

> solve({a*x^2=0},{x});

Наприклад, .