2. АЛГЕБРАЇЧНІ РІВНЯННЯ І СИСТЕМИ РІВНЯНЬ

2.1. Рівності, тотожності, рівняння

Рівністю називається два вирази, зв’язані знаком «=».

Властивості рівностей:

1)  ;

2) , ;

3)  ;

4)  ;

5)  .

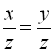
Рівності можуть бути числовими або зі змінними. Числові рівності можуть бути правильними чи неправильними. Наприклад, – правильна числова рівність; – неправильна числова рівність; – рівність зі змінними.

Алгебраїчна рівність може бути тотожністю або рівнянням. Якщо ліва частина рівності дорівнює правій при всіх допустимих значеннях букв, які входять до неї, то така рівність називається тотожністю, наприклад, .

Якщо ліва частина рівності дорівнює правій лише при певних значеннях букв, то така рівність називається рівнянням, а всі букви – невідомими. Наприклад, рівність є рівнянням з двома невідомими x і y.

Множина всіх допустимих значень букв, які належать алгебраїчній рівності, називається областю допустимих значень (ОДЗ) даної рівності. Наприклад, рівність 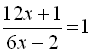визначена для будь-якого значення х, окрім того, де , тобто окрім . Отже, ОДЗ даної рівності є всі дійсні числа, окрім .

Рівнянням з однією змінною називається рівність виду , де і – деякі задані функції. Величина х називається невідомою. Коренем рівняння називається таке значення невідомого х, підстановка якого в обидві частини рівняння перетворює його на правильну числову рівність. Розв’язати рівняння – це значить знайти всі його корені або довести, що їх немає.

При розв’язуванні рівнянь часто застосовують різні перетворення. Якщо множина коренів перетвореного рівняння збігається з множиною коренів даного рівняння, то такі рівняння називаються рівносильними, а перетворення – рівносильними перетвореннями. Наприклад, перенесення з однієї частини рівняння в іншу алгебраїчних виразів з протилежними знаками, множення або ділення обох частин рівняння на число, відмінне від нуля, – рівносильні перетворення.

Два вирази, які з’єднані знаком рівності (=), являють собою самостійний тип даних Maple – рівняння (equation). Рівняння можна присвоювати звичайним змінним Maple, з ними можна здійснювати перетворення, використовуючи звичайні арифметичні дії, які виконуються окремо для лівої і правої частин рівнянь. Ці дії дозволяють перетворювати рівняння до виду, який зручний у використанні, а інколи і полегшують Maple пошук розв’язку.

Розглянемо декілька рівнянь з однією змінною.

Приклад 1. Рівняння не має коренів, оскільки при перенесенні невідомих в одну частину, а відомих в іншу – отримуємо неправильну числову рівність.

Приклад 2. Рівняння має три корені , , . – множина коренів рівняння.

Лінійні рівняння – це рівняння виду:

,                         (1)

де а і b – дійсні числа.

Рівняння (1) має один корінь, якщо : , звідки .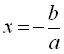

У рівнянні (1) при і х – будь-яке число. Наприклад, .

У випадку, коли , , рівняння розв’язків немає. Наприклад, .

Розглянемо лінійні рівняння або ті, що зводяться до лінійних.

Приклад 3. Розв’язати рівняння .

Розв’язання

.

Відповідь: .

Приклад 4. Розв’язати рівняння .

Розв’язання

Розкриємо дужки і зведемо подібні члени: .

Відповідь: .

Приклад 5. Розв’язати рівняння .

Розв’язання

. Оскільки отримана рівність не є правильною, тому дане рівняння розв’язків немає.

Відповідь: .

Приклад 6. Розв’язати рівняння .

Розв’язання

. Отримана рівність є правильною, тому рівняння має безліч коренів.

Відповідь: .

Приклад 7. Розв’язати рівняння .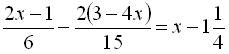

Розв’язання

Перенесемо все в одну частину і зведемо до спільного знаменника:

.

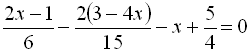
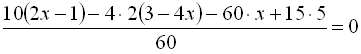
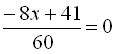
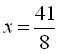Відповідь: .