6.10. Степенева функція з натуральним показником

Властивості степеневої функції з натуральним показником

1. .

2. , якщо (непарне); , якщо (парне).

3. При маємо . Значить, графік функції проходить через точку .

4. Функція парна при ; непарна при .

5. Функція набуває додатних значень при ; функція набуває від’ємних значень при та додатних значень при .

6. Функція зростає при , спадає при (рис. 6); функція зростає на всій області визначення (рис. 7).

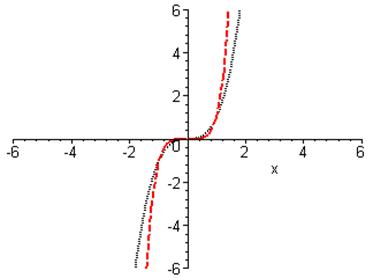
Побудуємо в Maple графіки степеневих функцій з парними та непарними натуральними показниками:

> plot([x^4,x^2],x=-6..6,-1..6);

> plot([x^5,x^3],x=-6..6,-6..6,color=[red,black],thickness=2,linestyle=[3,2]);

6.11. Степенева функція з цілим від’ємним показником

Властивості степеневої функції з цілим від’ємним показником ,

1.  .

2.  при ; при .

3. Нулів функція не має, .

4. Функція парна при ; непарна при .

5. Функція набуває лише додатних значень при ; функція набуває від’ємних значень при та додатних значень при .

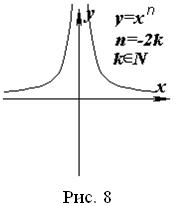
6. Функція , де , зростає при , спадає при (рис. 8); функція спадає на всій області визначення при .

6.12. Властивості функції 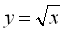та її графік

1.  .

2.  .

3. Функція має один нуль: при .

4. Функція ні парна, ні непарна, тобто загального виду.

5. Функція набуває додатних значень при .

6. Функція зростає на всій області визначення, тобто на проміжку .

7. Для побудови графіка складемо таблицю значень функції:

Команда plot() дає змогу побудувати графік за заданими точками. Побудуємо в Maple графік функції за складеною таблицею:

> plot([[0,0],[1,1],[4,2],[9,3]], x=-1..10,-1..5);

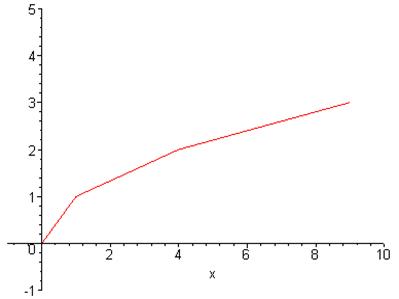
або за точками

> plot([[0,0],[1,1],[4,2],[9,3]], x=-1..10,-1..4,style=point,symbol=circle,symbolsize=20);

А тепер побудуємо в Maple графік функції , безпосередньо задаючи саму функцію:

> plot(sqrt(x),x=-1..10,-1..5);