6.13. Властивості функції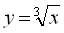 
і її графік
1. 
.
2. 
.
3. Функція має один нуль: 
при 
.
4. Функція непарна, оскільки 
, тобто 
і її графік симетричний відносно початку координат.
5. Функція набуває додатних значень при 
; функція набуває від’ємних значень при 
.
6. Функція зростає при 
.
7. Складемо таблицю значень функції:
|
0 |
1 |
8 |
|
|
|
0 |
1 |
2 |
|
|
Крім зазначеного раніше способу побудови графіка функції в системі Maple існує так званий smart-спосіб, через контекстне меню.
1) В командному рядку вводимо аналітичний вираз, який визначає функцію.
2) Виводимо його в стандартній математичній символіці.
3) Виділяємо і відкриваємо (клацаємо ЛКМ на виділеному виразі) контекстне меню.
4) Знаходимо в меню рядок Plot, переходимо по ньому на 2-D Plot і клацаємо ЛКМ – в наступній обчислювальній секції з’являється графік:
> y=surd(x,3);
> smartplot[x,y](y = surd(x,3));
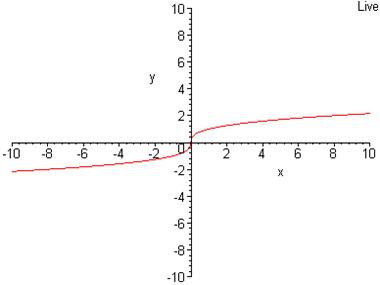
Звернемо увагу на те, що функція задана за допомогою функції surd. Хоча у системі Maple радикали задаються як результат піднесення до дробового степеня, в даному випадку це різні речі, оскільки функції та 
дещо відрізняються своїми властивостями.
> y=x^(1/3);
> smartplot[x,y](y = x^(1/3));
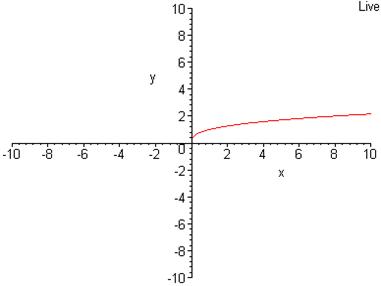
Даний графік називається smart-графіком.
Напис Live в області побудови графіка вказує на те, що область діюча, тобто можна продовжити роботу в ній. Наприклад, можна побудувати графік ще однієї функції. Тоді в наступний командний рядок вводиться функція, яку потрібно побудувати, і виводиться стандартний математичний вид. Отриманий вираз виділяється, «береться» «мишкою» і переміщується в область побудови графіка – область побудови доповнюється потрібним графіком.
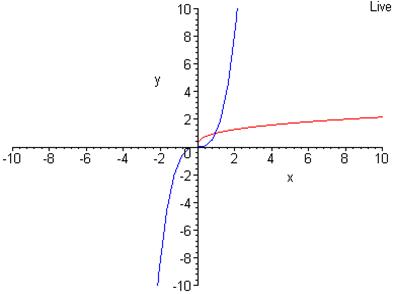
> y=x^3;
Переміщення краще проводити з натиснутою клавішею
