6.14. Функція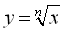

При парному п функція має такі ж властивості, що й функція , графік її нагадує графік функції . При непарному п функція має такі самі властивості, що й функція , і графік її нагадує графік функції .

6.15. Геометричні перетворення графіків функцій

Якщо відомий графік функції , то за допомогою геометрич-них перетворень можна побудувати графіки більш складних функцій.

Таблиця 3. – Геометричні перетворення графіків функцій

Приклад 7. Побудувати графік функції .

Розв’язання

Основним графіком для даного є графік . Потім будуємо графік функції , для цього зсуваємо графік на 1 одиницю праворуч вздовж осі . Далі будуємо , зсуваючи графік на 3 одиниці вгору вздовж осі .

Побудуємо графік функції smart-способом в Maple:

> y=x^2;

> smartplot[x,y](y = x^2);

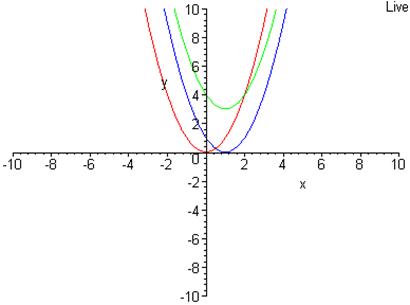
> y=(x-1)^2;

> y=(x-1)^2+3;

Приклад 8. Побудувати графік функції .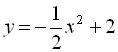

Розв’язання

Послідовно виконуємо такі побудови:

1) .

2) 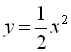(стискаємо вдвічі до осі графік функції ).

3) 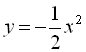(перевертаємо графік функції 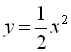відносно осі ).

4) 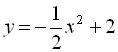(зсуваємо графік 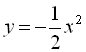вздовж осі на 2 одиниці вгору).

Побудуємо даний графік в системі Maple:

> plot([x^2,1/2*x^2,-1/2*x^2,-1/2*x^2+2],x=-10..10,-10..10,thickness=[1,2,2,3],linestyle=[3,2,1,0]);

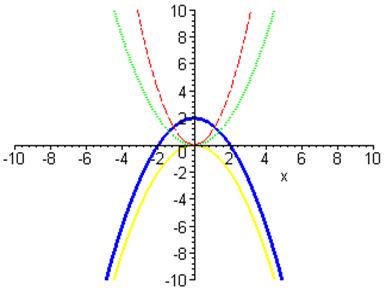
Тут можна прослідкувати, як перетворюється графік. Крім того, за допомогою вказання типу лінії та її товщини ми встановлюємо відповідність між функціями та їх графіками.