6.16. Способи побудови графіка квадратичної функції

1-й спосіб. Знаходження координат вершини параболи за форму-лами: 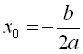; 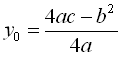та знаходження точок перетину параболи з осями координат.

Приклад 9. Побудувати графік функції .

Розв’язання

Тут , , , тоді ,

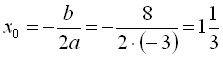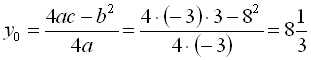. Отже, точка – вершина параболи. Знаходимо точки перетину параболи з осями координат:

з віссю 0х: , тобто 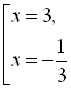. Отже точка і точка 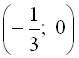– точки перетину параболи з віссю 0х;

з віссю 0y: , тобто . Це точка .

Крім того, відмітимо, що коефіцієнт – від’ємний, отже, парабола нахилена вітками донизу.

Відмічаємо на координатній площині знайдені точки і будуємо по них параболу (при потребі знаходимо додаткові точки).

2-й спосіб. Виділення повного квадрата квадратного тричлена.

В системі Maple будуємо графік функції :

> y=-3*x^2+8*x+3;

> smartplot[x,y](y = -3*x^2+8*x+3);

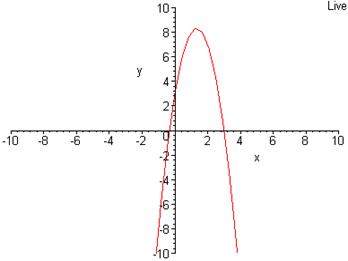
Приклад 10. Побудувати графік функції .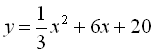

Розв’язання

Для побудови даного графіка функції виконаємо такі перетворення квадратного тричлена:

=

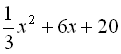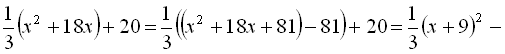
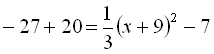. Тобто, потрібно побудувати графік функції 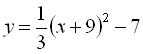. Для цього шляхом елементарних перетворень графік функції 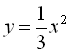зсуваємо вздовж осі 0х ліворуч на 9 одиниць і вниз на 7 одиниць вздовж осі 0y.

Побудуємо графік функції 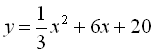smart-способом в Maple:

> y=1/3*x^2+6*x+20;

> smartplot[x,y](y = 1/3*x^2+6*x+20);

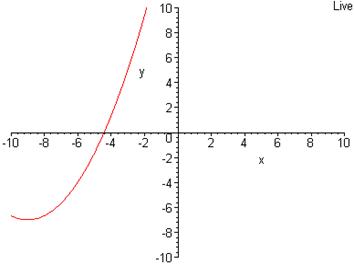
Недоліки smart-способу очевидні. Тут ми не можемо задати ні діапазон осей, ні колір, ні товщину лінії, тобто не вистачає опцій, які характеризують графік. Тому і графік у нас зображено частково.

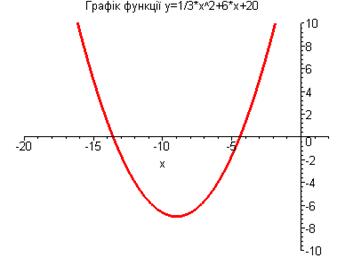
Тоді побудуємо даний графік із заданням діапазону і опцій:

> plot(1/3*x^2+6*x+20,x=-20..2,-10..10, thickness=3,title=`Графік функції y=1/3*x^2+6*x+20`);

Приклад 11. Побудувати графік функції .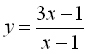

Розв’язання

1) Знайдемо область визначення функції 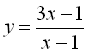: , тобто .

2) Перетворимо дану функцію до вигляду функції оберненої пропорційності: .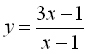

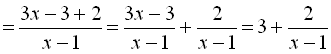3) Побудуємо графік функції 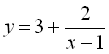за допомогою елементарних перетворень:

     1. Складаємо таблицю основних значень для функції 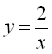і отримуємо дві вітки гіперболи, наносячи дані значення на координатну площину.

          2. Будуємо графік функції 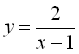, для цього зсуваємо графік 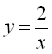вздовж осі 0х вправо на 1 одиницю.

          3. Піднімаючи графік функції 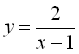на 3 одиниці вгору вздовж осі 0y, отримуємо графік функції .

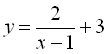> plot([2/x,2/(x-1),2/(x-1)+3],x=-10..10,-10..10,color=[black,red,brown],discont=true,linestyle=[3,1,0],thickness=[1,2,3]);

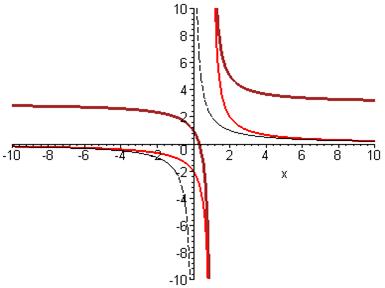
Звернемо увагу, що в даному прикладі ми додали ще одну опцію linestуle, яка визначає тип лінії графіка. Зміна типу лінії графіка досить зручна, наприклад, коли потрібно прослідкувати побудову графіка функції шляхом елементарних перетворень.