6.17. Приклади на побудову графіків функцій, які знаходяться під знаком модуля

Приклад 12. Побудувати графік функції .

Розв’язання

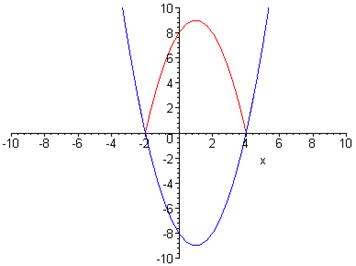
Будуємо спочатку графік функції . Для цього використовуємо спосіб виділення повного квадрата квадратного тричлена: . Далі шляхом елементарних перетворень будуємо спочатку графік функції , потім , а потім .

Для того, щоб побудувати графік функції , потрібно залишити без змін ту частину графіка , яка знаходиться над віссю 0х, а ту, що нижче, симетрично відобразити на верхню півплощину.

> plot([x^2-2*x-8,abs(x^2-2*x-8)],x=-10..10,-10..10, color=[blue,red]);

Приклад 13. Побудувати графік функції .

Розв’язання

Шляхом елементарних перетворень будуємо графік функції :

1.  (даний графік будуємо по основних точках).

2.  ().

3.  (відкидаємо ту частину графіка , яка у лівій півплощині відносно осі 0y, а ту, що у правій, залишаємо і симетрично відображаємо на ліву півплощину).

4.  (ту частину графіка , яка вище осі 0х, залишаємо без змін, а ту, що нижче, симетрично відображаємо на верхню півплощину).

> plot([x^2,x^2-4*x,x^2-4*abs(x),abs(x^2-4*abs(x))],x=-10..10,-10..10,linestyle=[3,2,0], color=[brown,green,blue,red],thickness=[1,2,2,4]);

Побудуємо той же графік без допоміжних графіків функцій:

> plot(abs(x^2-4*abs(x)),x=-10..10,-6..10);

Відмітимо, що графіки функцій, які містять модуль, можна будувати також, використовуючи означення модуля, як ми це робили у рівняннях та нерівностях з модулями.

Приклад 14. Побудувати графік функції .

Розв’язання

Прирівнюємо до нуля вирази, що знаходяться під знаком модуля: ; . Використовуючи означення модуля, маємо:

при ;

при ;

при .

Будуємо графік функції в системі Maple:

> plot(abs(x-2)+abs(2*x+3),x=-6..8,0..10);

Приклад 15. Побудувати графік функції .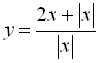

Розв’язання

. Оскільки дана функція містить два модулі з однаковими підмодулевими виразами х, то розглянемо випадки, коли підмодулевий вираз додатний та від’ємний (випадок, коли підмодулевий вираз дорівнює нулю, не розглядаємо згідно з областю визначення функції).

При ;

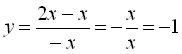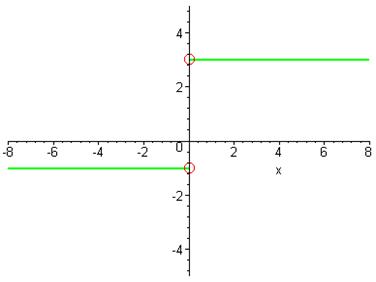
при . Отже, графіком функції 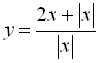є два промені:

> plot([(2*x+abs(x))/abs(x)],x=-8..8,-5..5,discont=true,color=[green],thickness=[2]);

g10:=%: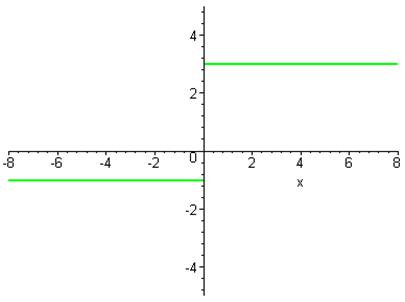

Щоб зобразити «виколоті» точки, потрібно у команді plot замість функції задати координати потрібних точок, а за допомогою опції style=[point] відобразити графік функції точками.

> plot([[[0,-1],[0,3]]],x=-8..8,-5..5,color=[red],style=[point],symbolsize=20,symbol=circle,thickness=[2]);g20:=%:

     Для того, щоб сумістити два попередні графіки на одному, застосовуємо команду display пакета plots. Структура даної команди має вигляд: plots[display](). В дужках через кому записуємо ті графіки, які потрібно сумістити на одному.

> plots[display]([g10,g20]);