6.8. Функція 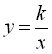та її графік

Функція виду 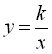, де – дійсне число, називається оберненою пропорційністю.

Основні властивості функції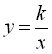

1.  , тому що на нуль ділити не можна.

2.  ,

3. Функція 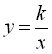непарна. Замінивши на , отримаємо 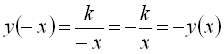, тобто . Відмітимо, що графік непарної функції симетричний відносно точки – початку координат.

4. Функція 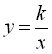не має нулів, оскільки рівняння не має коренів, графік функції 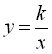не перетинає вісь .

5. Графік функції 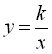називається гіперболою, яка складається з двох віток. Якщо , то вітки гіперболи розташовані в І і ІІІ координатних кутах, і функція є спадною (рис. 5); якщо , то вітки гіперболи розташовані в ІІ і ІV координатних кутах, і функція є зростаючою. Для прикладу оберненої пропорційності, коли , в системі Maple побудуємо графік функції :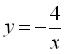

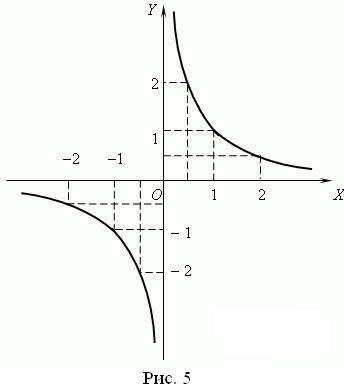
> plot(-4/x,x=-5..5,-5..5,color=blue,thickness=2, title=`Графік функції y=-4/x`);

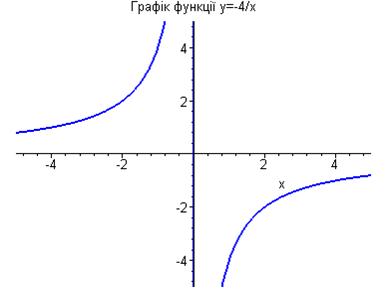
На графіку зображена деяка лінія на осі , яка не відповідає графіку гіперболи. Для того, щоб уникнути "вертикальних ліній" в точках, де функція змінює знак, додайте параметр "discont=true" до задання команди:

> plot(-4/x,x=-5..5,-5..5,color=blue,thickness=2, discont=true,title=`Графік функції y=-4/x`);

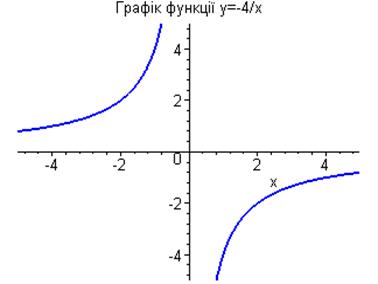
6.9. Квадратична функція та її графік

Функція, задана формулою , де , с – дійсні числа, називається квадратичною.

Основні властивості функції

1. , оскільки має зміст при будь-яких значеннях х.

2. .

3. Функція є функцією загального виду. Якщо , то – парна функція.

4. При і квадратична функція приймає вигляд . Графік цієї функції називається параболою. Графік проходить через точку , він симетричний відносно осі . Вітки параболи направлені вгору, якщо ; вниз, якщо .

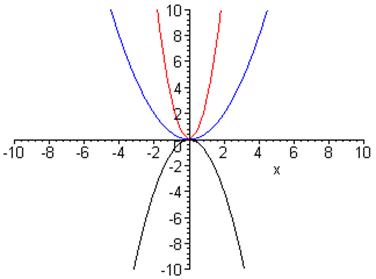
Щоб показати на одному графіку декілька функцій, потрібно в команді plot() задавати функції у вигляді списку, а значення опції color у вигляді списку дозволяють задати колір для виведення графіків функцій. Якщо опція color не задана, то Maple відображає функції у відповідності зі списком кольорів за замовчуванням. Покажемо на графіку декілька квадратичних функцій виду і прослідкуємо, як вони змінюються в залежності від параметра а:

> plot([3*x^2,-x^2,1/2*x^2],x=-10..10,-10..10,color=[red,black,blue]);

5. Графік функції також є параболою; він може бути отриманий з графіка функції шляхом паралельного перенесення (розглянемо пізніше на прикладі, як це робиться).