6.4. Монотонність функції

Функція називається зростаючою на даному числовому проміжку Х, якщо більшому значенню аргументу відповідає більше значення функції , тобто для будь-яких з

Функція називається спадною на даному числовому проміжку Х, якщо більшому значенню аргументу відповідає менше значення функції , тобто для будь-яких з

Функція, тільки зростаюча або тільки спадна на даному числовому проміжку, називається монотонною на цьому проміжку.

Прикладами монотонно зростаючих функцій є: , , . Прикладами монотонно спадних – , , 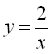. А, наприклад, функція не є монотонною на всій області визначення, оскільки при

вона є спадною, а при – зростаючою.

Приклад 4. Дослідити на монотонність функцію:

а) ;

б) , .

Розв’язання

а) Функція зростає на всій області визначення. Дійсно, . Нехай , тоді , отже .

б) Функція , спадає. Дійсно, нехай . Маємо

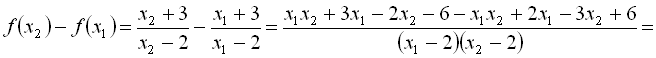
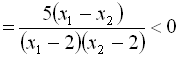, отже, .

6.5. Проміжки знакосталості і нулі функції

Числові проміжки, на яких функція зберігає свій знак (тобто залишається додатною або від’ємною), називаються проміжками знакосталості функції. Наприклад, для функції , при і при .

Значення аргументу , при яких функція , називаються нулями (або коренями) функції. Зрозуміло, що значення аргументу, при яких функція перетворюється в нуль, – це абсциси точок перетину графіка функції з віссю 0х.

6.6. Обернена функція

Кожному значенню рівність ставить у відповід-ність цілком певне значення . У деяких випадках рівність можна розглядати як таку, що кожному значенню ставить у відповідність цілком певне значення .

Приклад 5. Рівність кожному значенню ставить у відповідність . Можна сказати, що рівність визначає х як деяку функцію змінної тобто . Оскільки, звичайно, х позначає аргумент, а – функцію, то перепишемо залежність у вигляді . Функція є оберненою до функції .

Для того, щоб для функції при існувала обернена до неї функція, необхідно і достатньо, щоб функція була монотон-

ною при (тобто або тільки зростаючою, або тільки спадною).

Так, для функції оберненою є , . Для фун-

кції при оберненої не існує, однак при оберненою для є , а при оберненою для є функція .

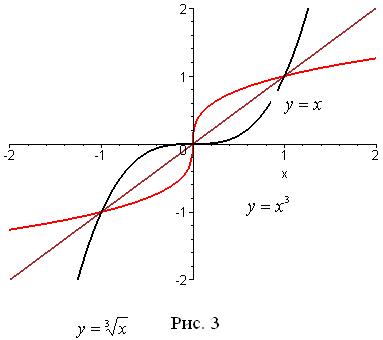
Якщо точка належить графіку функції , то точка належить графіку оберненої функції. Тому графіки прямої і оберненої функцій симетричні один одному відносно прямої . Так, наприклад, графік функції симетричний графіку функції відносно прямої (рис. 3). Узагалі для функції оберненою є .

Зауваження: Область визначення обе-рненої функції збіга-ється з множиною зна-чень прямої функції, а множина значень оберненої функції збігається з областю визначення прямої функції.

Приклад 6. Для функції знайти обернену.

Розв’язання

Виразимо х через :

. Замінивши х на та на х, маємо: . Отже, функція є оберненою до себе.

6.7. Лінійна функція та її графік

Функція, задана формулою , де k і b – дійсні числа, називається лінійною.

Основні властивості функції

1. , тобто вираз має зміст при будь-якому значенні х.

2. .

3. Функція є функцією загального виду, тобто не є ні парною, ні непарною. Замінимо на : , тобто . Як видно, та .

4. При функція приймає вигляд і називається прямою пропорційністю. Число називається коефіцієнтом пропорційності. Пряма пропорційність характеризується властивістю: «із збільшенням (зменшенням) значення х в декілька разів відповідне значення збільшується (зменшується) у стільки ж разів», тобто .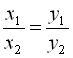

Функція є непарною. Її графік проходить через точку і являє собою пряму лінію.

5. Графік лінійної функції може бути отриманий з графіка функції паралельним перенесенням останнього на одиниць вздовж осі 0y. І оскільки графіком є пряма, то і графік функції є пряма лінія. Вона перетинає вісь 0y в точці , і нахилена до осі 0х під кутом , тангенс якого дорівнює , тобто . Якщо , то – гострий кут, якщо , то – тупий кут (рис. 4).

Побудуємо в системі Maple графік лінійної функції в першому випадку без вертикального діапазону та задання опцій, а в другому – із вказанням вертикального діапазону та деяких опцій:

> plot(x+3,x=-5..5);

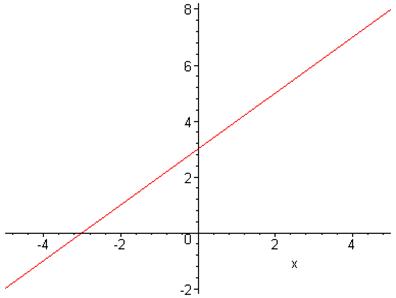
>plot(x+3,x=-10..10,-10..10,color=green, thickness=3,title=`Графік функції\ny=x+3`);

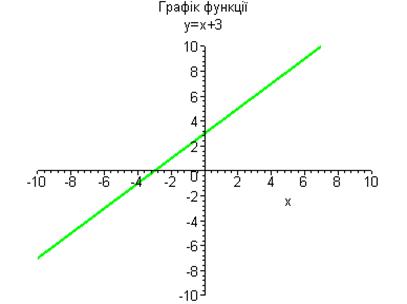
Відмінність очевидна.