Парні і непарні функції, періодичність функції

6.3. Парні і непарні функції, періодичність функції

Функція називається парною, якщо для будь-якого х з області визначення функції виконується рівність .

Функція називається непарною, якщо для будь-якого х з області визначення функції виконується рівність .

Якщо 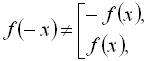то функція не є ні парною, ні непарною, або кажуть, що це функція загального виду.

Графіки парної та непарної функцій мають такі властивості:

якщо функція є парною, то її графік симетричний відносно осі ординат;

якщо функція є непарною, то її графік симетричний відносно початку координат.

Приклад 3. З’ясувати, чи дана функція парна, непарна, загального виду: а) ; б) ; в) .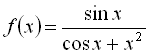

Розв’язання

а) , тобто функція – непарна.

б)

– парна функція.

в)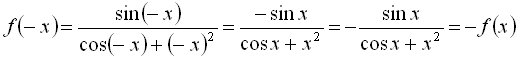

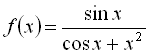– непарна функція.

Дослідити функцію на парність (непарність) у системі Maple поки що неможливо, але легко можна знайти для певної функції. До того ж можна побудувати графіки функцій та . Покажемо це на прикладі 3:

> restart;

> f:=x->4*x^6-3*x^4+5;

> f(-x);

> plot([f(x),f(-x)],x=-1.2..1.2,4..10,linestyle=[SOLID, DASH],color=black);

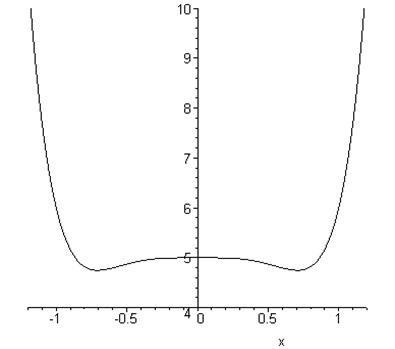
На побудованому графіку функцій та бачимо тільки одну лінію. До того ж графік функції здається симетричним відносно осі ординат. На основі чого можна припустити, що , адже ми знаємо, що графік парної функції симетричний відносно осі ординат, а графік непарної функції симетричний відносно початку координат. Ми говоримо “здається симетричним” тому, що на основі візуального спостереження можна робити тільки попередні припущення, які потрібно перевіряти аналітично.

Дійсно, графік функції теж здається симетричним відносно осі ординат, але насправді таким не є:

> f1:=x->4*x^6-3*x^4+5+0.0001*x;

plot([f1(x),f1(-x)],x=-1.2..1.2,4..10,linestyle=[SOLID, DASH],thickness=[1,1],color=black);

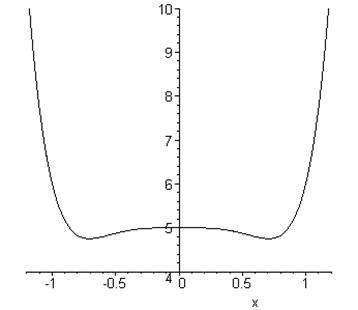
Пересвідчитись у парності функції легко за допомогою такої конструкції

> f(x)-f(-x);

тобто ,

> f1(x)-f1(-x);

тобто . Розглянемо ще одну функцію

> f2:=x->3*x^5-8*x^3;

> f2(-x);

> plot([f2(x),f2(-x)],x=-1.2..1.2,-6..6, linestyle=[SOLID, DASH],thickness=[1,1],color=black);

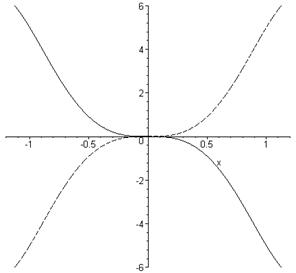
На побудованому графіку функцій та бачимо тільки дві лінії, які здаються симетричним відносно початку координат. Пересвідчимось у цьому:

> f(x)+f(-x);

тобто .

Функція називається періодичною, якщо існує таке число , що при будь-якому х з області визначення функції числа і також належать цій області і виконується рівність . Число Т в цьому випадку називається періодом функції .

Будь-яка періодична функція має нескінченну множину періодів, тому що якщо Т – період функції , то і число виду – період функції . На практиці, кажучи про період, нерідко мають на увазі найменший додатний період (якщо такий існує). Найменший додатний період називається основним періодом.

Прикладами періодичних функцій є тригонометричні.