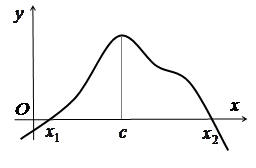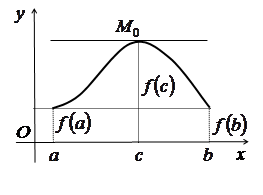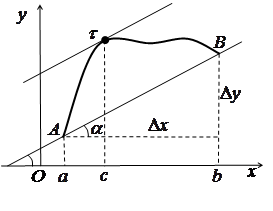3.5. Основні теореми диференціального числення

 

Теорема Ферма

Теорема 3.6. Нехай функція  визначена на інтервалі  і в деякій точці  має найбільше або найменше значення. Тоді якщо в точці  існує похідна, то вона дорівнює нулю, тобто .

Доведення. Нехай для визначеності функція  в точці  має найбільше значення. Оскільки ми прийняли, що  - найбільше значення, то  для довільної точки , звідки випливає, що (, якщо ) і (, якщо ).

Оскільки за умовою теореми похідна в точці  існує, то, перейшовши до границі за умови, що , дістанемо:

 

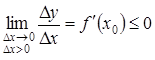 і .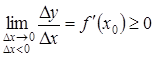

 

Але умови  і  виконуються одночасно, лише коли

.

 

Геометричний зміст теореми Ферма полягає в тому, що якщо в точці  диференційовна функція  має найбільше або найменше значення, то в точці  дотична до графіка функції  паралельна осі Ox.

 

Теорема Ролля

Теорема 3.7. Якщо функція

1) неперервна на відрізку ,

2) має рівні значення  на кінцях цього відрізка,

3) диференційовна в усіх точках інтервалу ,

то в цьому інтервалі існує принаймні одна точка , , в якій похідна функції дорівнює нулю

 

.

Доведення. Оскільки  неперервна на відрізку , то вона досягає на цьому відрізку свого найбільшого M і найменшого m значень (друга теорема Вейєрштраcса). Отже .

Розглянемо два можливі випадки: 1) ; 2) .

1) Нехай . Це можливо тільки за умови, що  для всіх , тоді для будь-якого  матимемо: .

2) Якщо . Тоді хоча б одне з цих значень М або m досягається всередині відрізка  в деякій точці , . Нехай для конкретності .

Оскільки ми прийняли, що  - найбільше значення і функція в точці с диференційовна, то за теоремою Ферма .

 

Зауваження. Між двома коренями функції завжди міститься корінь її похідної, якщо тільки функція задовольняє умови теореми Ролля (рис. 3.5).

 

Геометричний зміст теореми Ролля

 

Рис. 3.5

Рис. 3.6

 

Геометричний зміст теореми Ролля полягає в тому, що на графіку функції, яка задовольняє умови теореми, знайдеться принаймні одна точка , в якій дотична горизонтальна () (рис. 3.6).

 

Приклад 3.21. Перевірити справедливість теореми Ролля для функції  на відрізку .

Розв’язування. Перевіримо виконання умов теореми:

1)  – неперервна на відрізку ;

2) ;

3) .

Отже, як ми бачимо, умови теореми виконуються. Неважко помітити, що існує точка  в якій похідна дорівнює нулю .

 

Приклад 3.22. Довести, що друга похідна функції

 

 

принаймні в одній точці проміжку  дорівнює нулю.

Розв’язання. Очевидно, що функція диференційовна на всій числовій осі і перетворюється в нуль в точках , , . Тобто на кожному з відрізків  і  виконуються умови теореми Ролля. А отже  і  такі, що , . Але для функції  умови теореми Ролля на відрізку  також задовольняються: 1)  всюди неперервна; 2) ; 3)  диференційовна на всій числовій прямій (). Тому за теоремою Ролля , що , що і потрібно було довести.

 

Теорема Лагранжа (теорема про скінченні прирости)

Теорема 3.8. Якщо функція  

1) неперервна на відрізку ,

2) диференційовна в інтервалі ,

то в цьому інтервалі існує принаймні одна така точка , , що має місце рівність:

 

.                                   (3.18)

 

Доведення. Побудуємо допоміжну функцію , де . Підберемо  так, щоб функція  на кінцях відрізка мала рівні значення :

 

, .

 

.

 

Тоді

.

 

Функція  задовольняє умови теореми Ролля. Вона: 1) неперервна на , 2) , 3) диференційовна на . Отже, за цією теоремою знайдеться  таке, що .

Знайдемо похідну . Тоді з умови  матимемо, що , звідки , що і потрібно було довести.

 

 

Геометричний зміст теореми Лагранжа

 

Рис. 3.7

На рис. 3.7 зображено графік функції , яка задовольняє умови теореми Лагранжа на відрізку . Відмітимо, що є кутовим коефіцієнтом хорди, що стягує дугу АВ, яка відповідає приросту b-a. З іншого боку,  - кутовий коефіцієнт дотичної в точці з абсцисою , .

Отже, на гладкій дузі АВ графіка функції  завжди знайдеться принаймні одна внутрішня точка , в якій дотична паралельна хорді, що стягує кінці дуги А і В.

Зауваження. Теорему Лагранжа можна записати через прирости:

 

.                         (3.19)

 

Приклад 3.23. На дузі АВ кривої  знайти точку М, в якій дотична буде паралельна хорді, якщо , .

Розв’язання. Функція  неперервна і диференційовна для всіх значень х. За теоремою Лагранжа між двома значеннями  і  існує таке значення , що має місце рівність, отримана з (3.18)

,

де . Підставивши відповідні значення, дістанемо:

, ; .

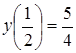Отже, маємо точку .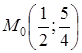

 

Теорема Коші (Cauchy theorem) (про відношення приростів двох функцій)

Теорема 3.9. Якщо функції  і

1) неперервні на відрізку ,

2) диференційовні в інтервалі , причому ,

то в цьому інтервалі існує точка ,  така, що має місце рівність:

 

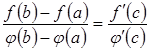.                               (3.20)

 

Доведення. Рівність (3.20) можлива, оскільки ,  .

Побудуємо допоміжну функцію , де . Підберемо  так, щоб функція  на кінцях відрізка мала рівні значення :

 

, .

 

.

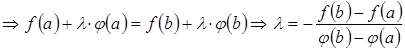Тоді

.

 

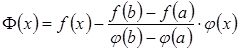Функція  задовольняє умови теореми Ролля. Отже за цією теоремою знайдеться таке , що .

Знайдемо похідну 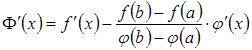. Тоді з умови  матимемо, що 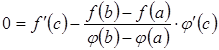, звідки

 

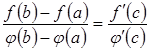, що і потрібно було довести.

 

Зауваження. Якщо в рівності (3.20) прийняти , то як наслідок отримаємо теорему Лагранжа (3.18).