3.11 Перевірка результатів аналітичного дослідження функцій за допомогою програмного пакета MathCad

 

Перевірку результатів аналітичного дослідження функцій зручно виконати за допомогою програмного пакета MathCad. Для цього необхідно скористатись панеллю «График». З її допомогою можна створювати різні дво- та тривимірні графіки, діаграми, подавати функцію двох змінних  у вигляді поверхні тривимірного простору.

Окрім того, дана панель також дозволяє побудувати графік функції, заданий в полярних координатах, проглянути  ділянки двовимірного графіка та прослідкувати еволюцію двовимірної кривої.

На рисунку 3.21 наведено стандартне поле графіка, яке з’являється при натисканні на кнопки , розташованої на панелі  «График». Далі необхідно заповнити комірки для функції та її аргументу. Функція відкладається вздовж осі ординат (вертикальна вісь), а її аргумент – вздовж осі абсцис.

Рис. 3.21

 

Заповнивши центральну комірку «» , що належить осі ординат, довільною функцією, і клацнувши мишкою в точці, яка розташована за межами поля графіка, можна миттєво отримати результат (рис. 3.22).

За замовчуванням система автоматично встановлює межі зміни абсциси і ординати. Абсциса в даному випадку змінюється від -10 до +10, в той час як ордината – від найбільшого до найменшого значення функції на вказаному інтервалі.

При необхідності можна самому встановлювати бажані межі змін абсциси та/або ординати. Для цього необхідно заповнити потрібними значеннями відповідні комірки, що позначені в полі графіка символом «». Форматування графіка виконується з діалогового вікна, що викликається правою кнопкою миші і не потребує особливих пояснень.

 

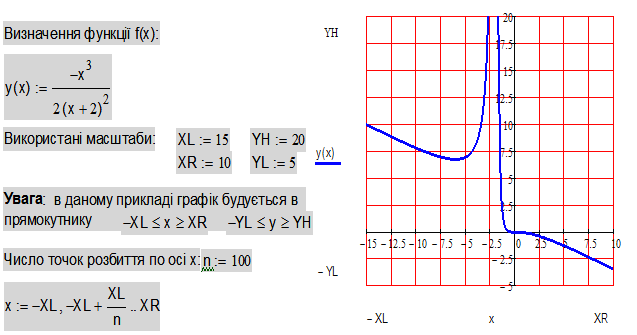
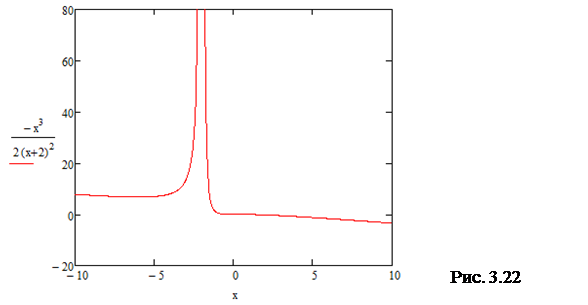
Приклад 3.45. Побудувати графік за допомогою MathCad  .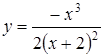

 

 

Рис. 3.23

Процес побудови графіка відображено на рис. 3.23.

 

 

 

Питання для самоперевірки

1.            Сформулюйте і доведіть теорему Ролля.

2.            У чому полягає геометричний зміст теореми Ролля?

3.            Яка з вимог теореми Ролля не виконується для функції ,  ?

4.            Сформулюйте і доведіть теорему Лагранжа.

5.            У чому полягає геометричний зміст теореми Лагранжа?

6.            Використовуючи формулу Лагранжа, доведіть нерівність: , при .

7.            Сформулюйте і доведіть теорему Коші.

8.            Сформулюйте і доведіть правило Лопіталя розкриття невизначеностей.

9.            В яких інших випадках можна застосовувати правило Лопіталя?

10.       Як можна розкривати за допомогою правила Лопіталя невизначеності , , , , ?

 

11.       Яка функція називається монотонною на проміжку Х ?

12.       Що називається точкою локального максимуму (мінімуму) функції?

13.       Сформулюйте і доведіть теорему про необхідну і достатню ознаки зростання (спадання) функції на проміжку Х.

14.       Сформулюйте і виведіть необхідну умову існування екстремуму?

15.       Які точки називаються критичними точками першого роду функції?

16.       Сформулюйте і доведіть першу достатню умову існування екстремуму функції.

17.       Сформулюйте і доведіть другу достатню умову існування екстремуму функції.

18.       Як відшукати інтервали монотонності і екстремуми функції?

19.       Як знайти найбільше і найменше значення функції, що неперервна на заданому відрізку?

20.       Чи може функція, що має найбільше і найменше значення, не мати точок локального екстремуму? Наведіть приклади.

21.       Чи може функція, що має точки локального екстремуму, не мати точок глобального екстремуму? Наведіть приклади.

22.       Графік якої функції називається опуклим (вгнутим) на проміжку?

23.       Яка точка на графіку функції називається точкою перегину?

24.       Сформулюйте і виведіть достатню умову опуклості графіка функції на проміжку Х.

25.       Що називається похилою асимптотою графіка функції? Як відшукати похилі асимптоти?

26.       Дати означення вертикальної асимптоти графіка функції.

27.       Яка загальна схема дослідження функції?