3.10 Приклади розв’язування типових завдань з дослідження функцій, заданих параметрично
Приклад 3.43. Дослідити функцію ![]() ,
, ![]() та побудувати її графік.
та побудувати її графік.
Розв’язання.
1. Функції ![]() та
та ![]() визначені
для всіх значень параметра
визначені
для всіх значень параметра ![]() та диференційовні в
усіх точках. Оскільки похідні
та диференційовні в
усіх точках. Оскільки похідні ![]() та
та ![]() не перетворюються на нуль одночасно, то
крива не має особливих точок.
не перетворюються на нуль одночасно, то
крива не має особливих точок.
2. З’ясуємо, чи має крива точки самоперетину. Маємо:
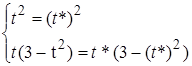 ,
,
оскільки передбачається, що ![]() та
та ![]() різні, то з першого рівняння випливає
різні, то з першого рівняння випливає ![]() . Підставляючи це значення в друге
рівняння, одержуємо
. Підставляючи це значення в друге
рівняння, одержуємо
![]() .
.
Якщо ![]() , то
, то ![]() і ми одержали два однакових параметра,
що неможливо. Залишається єдино можливий варіант:
і ми одержали два однакових параметра,
що неможливо. Залишається єдино можливий варіант: ![]() ,
, ![]() . Цим значенням відповідає одна точка
. Цим значенням відповідає одна точка ![]() . З’ясуємо значення кутових коефіцієнтів
дотичних для
. З’ясуємо значення кутових коефіцієнтів
дотичних для ![]() та
та ![]() :
:
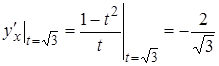 ,
,
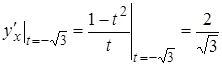 .
.
Оскільки кутові коефіцієнти відрізняються, то через точку
![]() крива проходить двічі, тобто це є точка
самоперетину.
крива проходить двічі, тобто це є точка
самоперетину.
3. Маємо значення кутового коефіцієнта дотичної 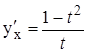 .
Оскільки
.
Оскільки ![]() при
при ![]() , то
дотична паралельна осі абсцис в точках
, то
дотична паралельна осі абсцис в точках 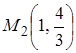 та
та 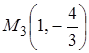 .
. ![]() при
при ![]() , тому в точці
, тому в точці ![]() дотична
паралельна осі ординат.
дотична
паралельна осі ординат.
4. Оскільки ![]() ,
, ![]() , маємо
, маємо
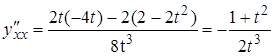 ,
,
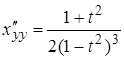 .
.
Якщо ![]() , то опуклість кривої
спрямована в додатну сторону осі ординат. При
, то опуклість кривої
спрямована в додатну сторону осі ординат. При ![]() крива
змінює характер опуклості, але тут немає перегину, оскільки в цій точці дотична
паралельна осі ординат і ми повинні розглядати рівняння виду
крива
змінює характер опуклості, але тут немає перегину, оскільки в цій точці дотична
паралельна осі ординат і ми повинні розглядати рівняння виду ![]() . Оскільки
. Оскільки 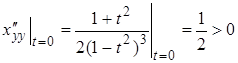 , то опуклість кривої
спрямована у від’ємну сторону осі абсцис.
, то опуклість кривої
спрямована у від’ємну сторону осі абсцис.
5. Асимптот крива не має.
· З рівняння кривої видно, що вона симетрична відносно
осі абсцис: при зміні знака параметра t
змінюється лише знак ординати та зберігається знак абсциси (![]() ). Це означає, що достатньо побудувати
криву тільки для додатних значень параметра t. Складемо допоміжну
таблицю значень опорних точок:
). Це означає, що достатньо побудувати
криву тільки для додатних значень параметра t. Складемо допоміжну
таблицю значень опорних точок:
|
t |
x |
y |
Точка та її особливості |
|
0 |
0 |
0 |
M4 (дотична паралельна осі ординат, опуклість спрямована у від’ємну сторону осі абсцис |
|
1 |
1 |
|
M2 (дотична паралельна осі абсцис) |
|
|
3 |
0 |
M1(точка самоперетину) |
|
2 |
4 |
|
M5 |
Крива зображена на рис. 3.19.

Рис. 3.19
Приклад 3.44. Дослідити функцію ![]() ,
, ![]() та побудувати її графік.
та побудувати її графік.
Розв’язання.
1. Функції ![]() та
та ![]() визначені
для всіх значень параметра
визначені
для всіх значень параметра ![]() та диференційовні в
усіх точках.
та диференційовні в
усіх точках. ![]() Оскільки
Оскільки ![]() ,
, ![]() ,
то система
,
то система 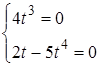 сумісна при
сумісна при ![]() .
Отже, точка
.
Отже, точка ![]() буде особливою точкою. З’ясуємо її
характер.
буде особливою точкою. З’ясуємо її
характер.
![]() ,
,
![]() ,
, ![]() ,
отже
,
отже ![]() . Тоді
. Тоді ![]() і
і ![]() . Таким чином, точка
. Таким чином, точка ![]() є точкою звороту другого роду.
є точкою звороту другого роду.
2. Точок самоперетину немає, оскільки система 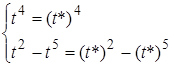 несумісна.
несумісна.
3. Оскільки кутовий коефіцієнт дотичної 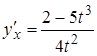 , то
дотична паралельна осі ординат при
, то
дотична паралельна осі ординат при ![]() (в точці звороту).
Дотична паралельна осі абсцис при
(в точці звороту).
Дотична паралельна осі абсцис при ![]() , тобто в точці
, тобто в точці ![]() .
.
4. Знаходимо 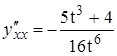 . В околі нуля
. В околі нуля ![]() , тобто крива опукла вверх. Оскільки
, тобто крива опукла вверх. Оскільки ![]() при
при ![]() і
при
і
при ![]() маємо
маємо ![]() , то
крива опукла вверх; при
, то
крива опукла вверх; при ![]() маємо
маємо ![]() – крива опукла вниз (угнута). Таким
чином, точка
– крива опукла вниз (угнута). Таким
чином, точка ![]() – точка перегину кривої.
– точка перегину кривої.
5. Крива асимптот немає.
6. Характерних особливостей крива не має. Складемо допоміжну таблицю значень опорних точок:
|
t |
x |
y |
Точка та її особливості |
|
0 |
0 |
0 |
M1 (точка звороту другого роду) |
|
|
0,2947 |
0,3257 |
M2 (дотична, паралельна осі абсцис) |
|
|
0,7426 |
1,55 |
M3 (точка перегину кривої) |
|
1 |
1 |
0 |
M4 |
|
-1 |
1 |
2 |
M5 |
|
2 |
16 |
-28 |
M6 |
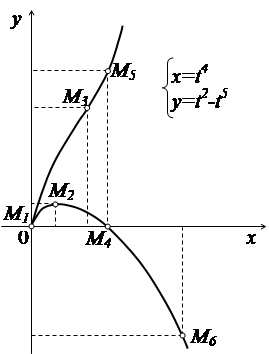 |
Крива зображена на рисунку 3.20.
Рис. 3.20