3.9 Схема дослідження функцій, заданих параметрично
1. Визначають
область регулярності кривої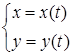 
та її особливі точки
(singular point, singularity).
Означення 3.12. Точка 
називається особливою
точкою кривої 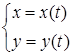, якщо параметр 
є розв’язком системи 
.
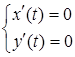Для з’ясування характеру особливої точки необхідно
знайти порядок першої відмінної від нуля похідної функцій 
та 
при 
.
Нехай 
, 
;
,
.
Тоді можливі чотири випадки:
1)
якщо 
– непарне, а 
–
парне, то в околі точки крива поводить себе
так само, як і в околі регулярної точки;
2)
якщо та –
непарні, то – точка перегину;
3)
якщо – парне, а –
непарне, то – точка звороту першого роду (рис.
3.18,а);
4)
якщо та –
парні, то – точка звороту другого роду (рис.
3.18,б).
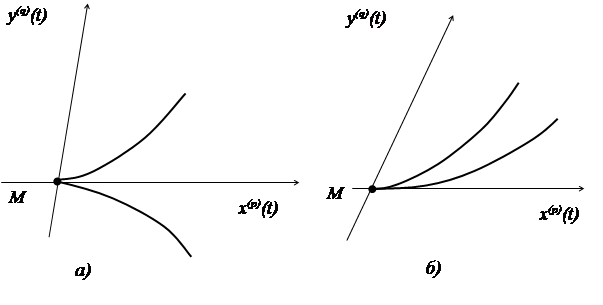
Рис. 3.18
2. Знаходять точки самоперетину кривої.
Означення 3.13. Точка 
називається точкою
самоперетину кривої (self-intersection point of curve), якщо цій точці відповідають різні значення параметра і крива функції 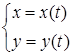проходить через дану точку декілька
разів. Параметри точки самоперетину є розв’язками системи: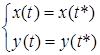
.
3. Знаходять точки, в яких дотичні паралельні координатним осям.
Оскільки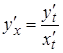 
,
то:
1)
дотична паралельна осі 
, якщо 
;
2)
дотична паралельна осі 
, якщо 
.
4. Знаходять точки перегину та інтервали опуклості.
Дослідження параметрично заданої функції на опуклість
аналогічне дослідженню функції 
з врахуванням формул
,
.
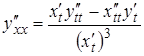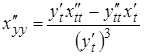5. Визначають асимптоти
Означення 3.14. Пряму 
називають похилою
асимптотою графіка функції 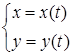, якщо 
, 
.
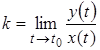Означення 3.15. 
називається
вертикальною асимптою, якщо
, при цьому 
.
Означення 3.16. 
називається
горизонтальною асимптотою, якщо 
, при цьому 
.
6. Відмічають деякі загальні властивості кривої (наприклад, симетрію відносно будь-якої осі). Для полегшення побудови кривої знаходять декілька опорних точок (наприклад, точки перетину з осями координат).