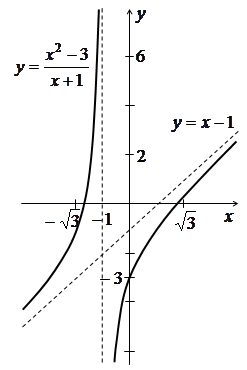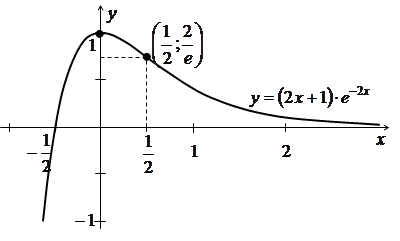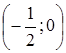3.8 Приклади розв’язування типових завдань з дослідження функцій, заданих явно

 

Приклад 3.40. Дослідити функцію 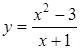 та побудувати її графік.

Розв’язання.

1) Функція визначена для всіх . Функція загального виду, оскільки . Функція не є періодичною.

2) В точці  функція має розрив.

Оскільки 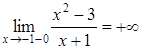, , 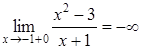то точка  є точкою розриву другого роду типу „нескінченний стрибок”.

3,а) Враховуючи дослідження пункту 2), робимо висновок, що пряма  є вертикальною асимптотою.

3,б) Шукаємо похилі асимптоти у вигляді . Тут ,  відповідають випадку , а ,  - випадку . Знайдемо невідомі коефіцієнти ,  за формулами (3.24), (3.25)

 

,

 

.

 

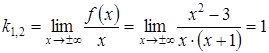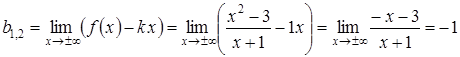Отже,  одна і та ж сама похила асимптота як при , так і при .

4) Для визначення інтервалів монотонності та локальних екстремумів обчислимо спочатку похідну

 

.

 

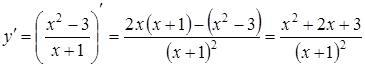Знайдемо проміжки знакосталості для .

Рівняння  дійсних коренів не має, причому . Врахувавши те, що знаменник , робимо висновок, що  на кожному з проміжків неперервності. Отже дана функція зростає при  і при . Точок локального екстремуму немає.

5) Знайдемо проміжки опуклості (вгнутості).

Для цього обчислимо спочатку :

 

.

 

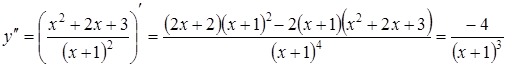Рис. 3.15

Знайдемо проміжки знакосталості для . За методом інтервалів отримуємо, що  при  - тут графік функції вгнутий, та  при  - тут графік функції опуклий. В самій точці  функція невизначена, тому точки перегину немає. 6) Знайдемо точки перетину графіка з координатними осями. Графік функції перетинає вісь абсцис, якщо , отже, маємо точки: . Графік перетинає вісь ординат, якщо , маємо точку .

 

7) У відповідності з проведеним дослідженням будуємо ескіз графіка даної функції (див. рис. 3.15).

Приклад 3.41. Дослідити функцію  та побудувати її графік.

Розв’язання.

1) Функція визначена на всій числовій осі. Функція не є парною, оскільки ; не є непарною, оскільки . Функція не є періодичною.

2) Функція неперервна на всій числовій осі.

3,а) Оскільки функція є неперервною, вертикальних асимптот немає.

3,б) Шукаємо похилі асимптоти у вигляді . Тут ,  відповідають випадку , а ,  - випадку . Знайдемо невідомі коефіцієнти ,  за формулами (3.24), (3.25).

.

 

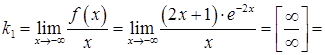
Отже, похилої асимптоти при  (зліва) не існує.

,

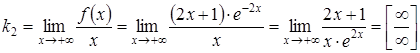за правилом Лопіталя:

;

 

,

 

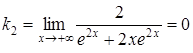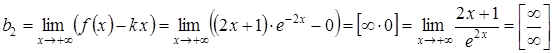за правилом Лопіталя:

.

 

Отже,  - похила асимптота при  (права горизонтальна асимптота).

4) Для визначення інтервалів монотонності та локальних екстремумів спочатку обчислимо похідну

.

Знайдемо проміжки знакосталості для .

Рівняння  має єдиний корінь  (єдина критична точка). За методом інтервалів отримуємо, що  при  - на цьому інтервалі функція зростає і  при  - тут функція спадає. Оскільки при переході через точку  похідна змінює знак з „+” на „-”, то  є точкою локального максимуму, .

5) Визначимо інтервали опуклості (вгнутості) і точки перегину.

Для цього обчислимо спочатку :

.

 

Знайдемо проміжки знакосталості для .

Рівняння  має єдиний корінь . За методом інтервалів отримуємо, що при ,  - тому на цьому інтервалі графік функції опуклий; при ,  - графік угнутий.

Оскільки при переході через точку  друга похідна змінює знак, то  є точкою перегину; 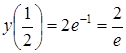. Перегин: .

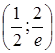6) Знайдемо точки перетину графіка з координатними осями.

 

Рис. 3.16

Графік функції перетинає вісь абсцис, якщо ,  отже, маємо точку . Графік перетинає вісь ординат, якщо , маємо точку .

7) За результатами дослідження будуємо ескіз графіка даної функції (рис. 3.16).

Приклад 3.42. Дослідити функцію 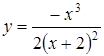 та побудувати її графік.

Розв’язання.

1) Функція визначена для всіх . Функція не є парною, оскільки ; не є непарною, оскільки . Функція не є періодичною.

2) Функція неперервна на кожному з інтервалів , . В точці  функція має розрив.

Оскільки

 

, ,

 

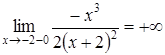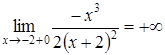то точка  є точкою розриву другого роду типу „нескінченний стрибок”.

3,а) Враховуючи пункт 2), робимо висновок, що пряма  є вертикальною асимптотою.

3,б) Шукаємо похилі асимптоти у вигляді . Тут ,  відповідають випадку , а ,  - випадку . Знайдемо невідомі коефіцієнти ,  за формулами (3.24), (3.25).

 

;

 

 

.

 

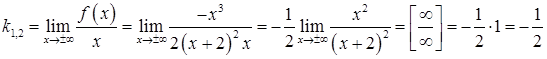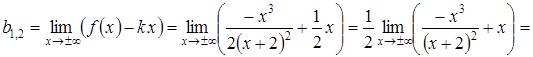
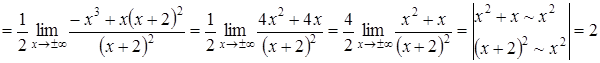Отже, пряма  є похилою асимптотою як при , так і при .

Знайдемо точку перетину графіка (якщо це можливо) з похилою асимптотою:

, .

 

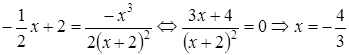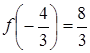Маємо точку перетину .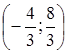

4) Визначимо інтервали монотонності та точки локального екстремуму. Спочатку обчислимо похідну

 

.

 

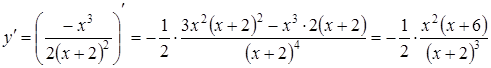Знайдемо проміжки знакосталості для  за методом інтервалів.

Рівняння  має корені  та  (критичні точки першого роду). Похідна не існує в точці , але оскільки ця точка не належить області визначення, то вона не є критичною (у ній не може бути екстремуму).

За методом інтервалів складаємо таблицю зміни знаків похідної

 

 

У точці  функція має локальний мінімум, оскільки при переході значень аргументу через неї похідна змінює знак з „-” на „+”, .

У точці  функція не має локального екстремуму.

5) Визначимо інтервали опуклості (вгнутості) і точки перегину.

Для цього обчислимо спочатку другу похідну :

 

 

.

 

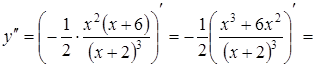
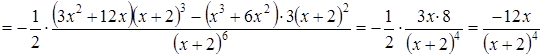Знайдемо проміжки знакосталості для .

Похідна дорівнює нулю при  (критична точка другого роду) і не існує при  (проте  не є критичною точкою, тому що функція в ній не існує).

За методом інтервалів складаємо таблицю зміни знаків похідної

 

 

При ,  , тому на цих інтервалах графік функції вгнутий; при   графік опуклий.

Оскільки при переході значень аргументу через точку  друга похідна змінює знак, то  є точкою перегину; . Отже, перегин .

6) Точка перетину графіка з віссю абсцис (ординат)  вже знайдена.

7) За результатами дослідження будуємо ескіз графіка даної функції (рис. 3.17).

 

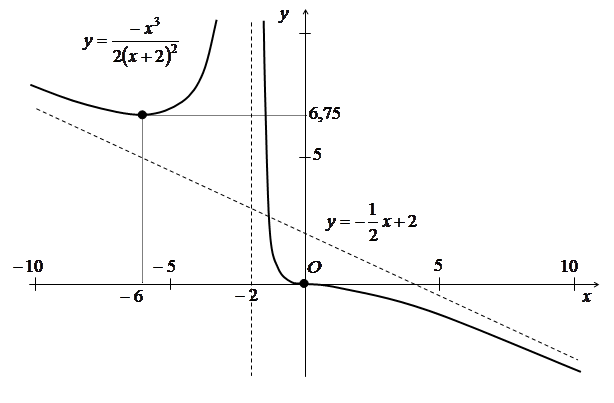
Рис. 3.17