2.4. Порівняння н. м. функцій
Нехай функції ![]() - н.
м. при
- н.
м. при ![]() , тобто
, тобто ![]() і
і ![]() . Складемо відношення
. Складемо відношення ![]() .
.
1. Якщо 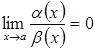 ,
то
,
то ![]() називається н. м. вищого порядку (high order infinitesimal) (н. м. вищого порядку малості), ніж
називається н. м. вищого порядку (high order infinitesimal) (н. м. вищого порядку малості), ніж ![]() при
при ![]() . Це
записують так:
. Це
записують так: ![]() („o” маленьке від
(„o” маленьке від ![]() ).
).
2. Якщо 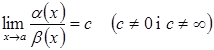 ,
то
,
то ![]() і
і ![]() називаються
н. м. одного порядку (equal order infinitesimals) при
називаються
н. м. одного порядку (equal order infinitesimals) при ![]() . Це
записують так:
. Це
записують так: ![]() („O” велике від
(„O” велике від ![]() ).
).
3. Якщо 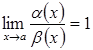 , то
, то ![]() і
і ![]() називаються
еквівалентними н. м. (equivalent infinitesimal) при
називаються
еквівалентними н. м. (equivalent infinitesimal) при ![]() . Це
записують так:
. Це
записують так: ![]() .
.
Таблиця еквівалентних н. м. функцій (![]() ).
).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема 2.9. Н. м. функції ![]() і
і ![]() будуть еквівалентними (
будуть еквівалентними (![]() ) при
) при ![]() тоді
і тільки тоді, коли їх різниця
тоді
і тільки тоді, коли їх різниця ![]() є
є
н. м. вищого порядку, ніж н. м. ![]() і
і ![]() при
при![]() .
.
Доведення. Необхідність. Нехай н. м. ![]() (або
(або 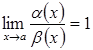 ) при
) при ![]() . Доведемо, що їх різниця
. Доведемо, що їх різниця ![]() є н. м. вищого порядку, ніж н. м.
є н. м. вищого порядку, ніж н. м. ![]() і
і ![]() при
при![]() . Для цього розглянемо границю:
. Для цього розглянемо границю:
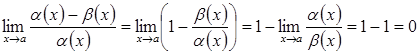 .
.
А отже ![]() є н. м. вищого порядку, ніж н.
м.
є н. м. вищого порядку, ніж н.
м. ![]() при
при![]() .
.
Достатність. Доведемо, що якщо різниця ![]() є н.
м. вищого порядку, ніж н. м.
є н.
м. вищого порядку, ніж н. м. ![]() при
при![]() , то
, то ![]() .
Дійсно
.
Дійсно
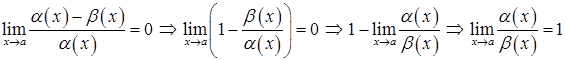 ,
,
тому ![]() при
при ![]() . Цілком аналогічно доводиться, що якщо
різниця
. Цілком аналогічно доводиться, що якщо
різниця ![]() є н. м. вищого порядку, ніж н. м.
є н. м. вищого порядку, ніж н. м. ![]() при
при ![]() , то
, то ![]() .
.
Теорема 2.10. Якщо н. м. ![]() ,
, ![]() при
при ![]() , то
справедлива рівність
, то
справедлива рівність
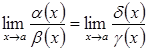 .
.
Доведення. Дійсно
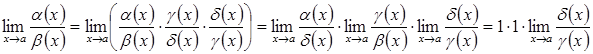 .
.
Зауваження. Теорема 2.10 дає можливість замінювати під знаком границі н. м. множники та дільники на еквівалентні (н. м. доданки замінювати на еквівалентні в загальному випадку не можна).
При порівнянні нескінченно
великих (н. в.) функцій мають місце аналогічні правила порівняння. Наприклад,
дві н. в. функції ![]() і
і ![]() називаються
еквівалентними (equivalent) при
називаються
еквівалентними (equivalent) при ![]() , якщо
, якщо
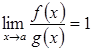 .
.
Так, при ![]() має місце
еквівалентність:
має місце
еквівалентність:
|
|
тому при обчисленні границі відношення двох многочленів на нескінченності ми можемо замінити вираз під знаком границі на еквівалентне відношення старших степенів многочленів, взятих зі своїми коефіцієнтами.