2.5. Основні теореми про границю

 

Теорема 2.11. Границя сталого дорівнює сталому, тобто

, де .

Доведення. Нехай , де . Розглянемо різницю , маємо:  – нескінченно мала величина. За теоремою 2.4 маємо, що .

 

Теорема 2.12. Границя суми дорівнює сумі границь.

 

Доведення. Нехай, наприклад, , . Покажемо, що . Дійсно

;

 

.

 

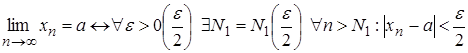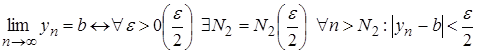За  оберемо  та оцінимо модуль , маємо:

.

Таким чином,

 

.

Зауваження. Випадок суми довільного скінченного числа числових послідовностей доводиться аналогічно.

 

Теорема 2.13. Границя добутку дорівнює добутку границь.

 

Доведення. Нехай, наприклад, , . Покажемо, що . Дійсно, якщо , то за теоремою 2.3 , де  – нескінченно мала величина. Аналогічно, , де  – нескінченно мала. Тоді

 

.

 

Оскільки константа є величиною обмеженою, то за теоремою 2.6 величини  є нескінченно малими; за теоремою 2.5 величина  також є нескінченно малою. Оскільки сума трьох нескінченно малих величин є нескінченно малою, то  є нескінченно мала і за теоремою 2.4.

 

Зауваження

1)    Сталий множник можна виносити за знак границі.

 

Дійсно,

.

 

 

2) .

Дійсно,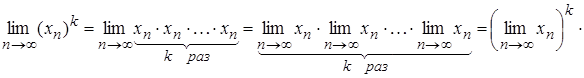

 

 

3) .

 

 

Теорема 2.14. Границя частки двох послідовностей дорівнює частці границь цих послідовностей, якщо границя знаменника не дорівнює нулю, тобто

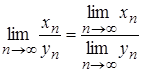, де .

 

 

Зауваження. Доведення даної теореми проводиться аналогічно доведенню теореми 2.13.

 

Теорема 2.15.

1) , де ;

2) , де .

Теорема 2.16. Якщо для послідовності  відомо, що для всіх   і , то .

Доведення. Проведемо доведення методом від супротивного. Нехай , але тоді  і . Остання рівність суперечить умові теореми. Це означає, що наше припущення хибне і .

 

Теорема 2.17. Якщо для послідовностей  та  відомо, що , то .

Доведення. За умовою теореми , тоді за теоремою 2.16

 

.

 

Теорема 2.18. .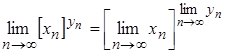

 

Запам’ятай добре! Аналогічні теореми мають місце для границь функцій в точці.