2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, ... .
Це – послідовність парних натуральних чисел. Число 2 – її перший член, 4 – другий, 6 – третій, 20 – десятий і т. д.
Приклади числових послідовностей :
1, 2, 3, 4, 5, ... – послідовність натуральних чисел,
1, 3, 5, 7, 9, ... – послідовність непарних (непарний – odd) натуральних чисел.
Послідовності бувають скінченні (скінченний – finite) і нескінченні (нескінченний – infinite). Скінченною, наприклад, є послідовність одноцифрових натуральних чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9.
Послідовність усіх натуральних чисел нескінченна. Записуючи нескінченну послідовність, після кількох її перших членів ставлять трикрапку.
Перший, другий, третій члени послідовності парних натуральних чисел дорівнюють відповідно 2, 4, 6. Пишуть: a1=2, a24, a3=6. Оскільки кожний член послідовності парних натуральних чисел удвоє більший від свого порядкового номера, то її n-й член дорівнює 2n, тобто
an=2n.
Це формула n-го члена послідовності парних натуральних чисел.
an=2n-1 формула n-го члена послідовності непарних натуральних чисел. Якщо відома формула n-го члена послідовності, то неважко обчислити будь-який її член. Напишемо кілька перших членів послідовності, n-й член якої an=n2+2. Надаючи змінній n значення 1, 2, 3, 4, 5, ..., отримаємо перші члени послідовності: 3, 6, 11, 18, 27, 38, 51, ... .
Тисячний член цієї послідовності a1000=10002+2=1000002.
Набагато важче розв'язувати обернену задачу – для даної послідовності знайти її n-й член. Наприклад, формула n-го члена послідовності простих чисел 2, 3, 5, 7, 11, 13, ... – невідома і досі, хоч математики шукали її понад 2000 років.
Із двох сусідніх членів ai і ai+1 послідовності член ai+1 називають наступним (наступний – next) за ai, а ai – попереднім (попередній – previous) відносно ai+1. Послідовність називають зростаючою, якщо кожний її член, починаючи з другого, більший від попереднього. Послідовність називається спадною, якщо кожний її член, починаючи з другого, менший від попереднього.
Арифметичною прогресією називається послідовність, кожний член якої, починаючи з другого, дорівнює попередньому члену, до якого додають одне й те саме число:
a1, a1+d, a1+2d, a1+3d, ... .
Число d називається різницею арифметичної прогресії (різниця арифметичної прогресії – common difference). Число a1 називається першим членом арифметичної прогресії.
Перший член і різниця арифметичної прогресії можуть бути якими завгодно числами. Арифметична прогресія зростаюча, якщо її різниця додатна або спадна, якщо її різниця від'ємна.
Формула n-го члена арифметичної прогресії an=a1+(n-1)d.
Сума членів скінченної арифметичної прогресії дорівнює півсумі крайніх її членів, помноженій на число членів:
![]()
Геометричною прогресією називається послідовність, кожний член якої, починаючи з другого, дорівнює попередньому члену, помноженому на одне й те саме число: b1, b1q, b1q2, b1q3, ... .
Число q називають знаменником геометричної прогресії (зна-менник геометричної прогресії – geometric ratio). Число b1 називається першим членом геометричної прогресії.
Перший член b1 і знаменник q геометричної прогресії можуть бути будь-якими числами.
Формула n-го члена геометричної прогресії: bn=b1qn-1.
Формула суми n перших членів геометричної прогресії з першим членом b1 і знаменником q
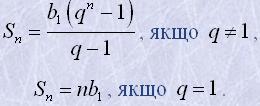
Вправи
1. Написати кілька перших членів послідовності квадратів натуральних чисел. Який її n-й член?
2. Написати кілька перших членів і n-й член послідовності кубів натуральних чисел.
3. Знайти шостий, восьмий і десятий члени послідовності, n-й член якої bn=2n.
4. Перший член послідовності дорівнює 1/2, a кожний інший вдвічі більший від попереднього. Написати сім перших членів послідовності.
5. Перші два члени послідовності 1 і 3, а кожний інший дорівнює сумі двох попередніх її членів. Напи¬сати 10 перших членів цієї послідовності.
6. Написати сім перших членів арифметичної прогресії, у якої:
а) a1=2, d=5;
б) a1=-3, d=4.
7. В арифметичній прогресії a1=9, d=4. Знайти a15, a32.
8. a1, a2, a3 – арифметична прогресія. Знайти a30, якщо a3=3, a4=4.
9. Знайти суму перших ста натуральних чисел.
10. Знайти суму перших ста непарних натуральних чисел.
11. Знайти арифметичну прогресію, що складається з натуральних чисел, якщо добуток перших трьох та перших чотирьох її членів відповідно дорівнюють 6 та 24.
12. Знайти перший член і різницю арифметичної прогресії, якщо
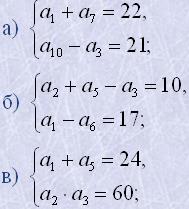 |
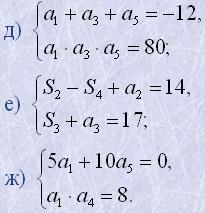 |
13. Розв'язати рівняння:
а) 0,32+4+6+...+2x=0,372;
б) 33·35·38·...·32n-1=275;
в) 22·24·26·...·22n=0,25-28;
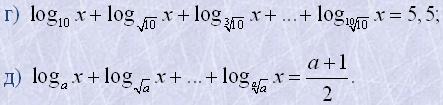
14. Написати сім перших членів геометричної прогресії, у якої b1=1, q=3.
15. b1, b2, b3, ...– геометрична прогресія. Знайти b12, якщо b3=1, b4=0,5.
16. Знайти суму 15 перших членів геометричної прогресії
а) 1, 2, 4, 8, ...;
б) 1024, 512, 256, ... .
17. Було це майже сто років тому. Селянин продавав 20 овець за 200 грн. Коли один з покупців став надто довго торгуватись, селянин за-пропонував: «Дай за першу вівцю 1 коп., за другу – 2 коп., за третю – 4 коп. і далі за кожну вівцю вдвічі більше копійок, ніж за попередню». Покупець погодився. Скільки він заплатив за тих 20 овець?
18. Задача з індійського фольклору. Цар дуже любив шахи і обіцяв винахідникові гри дати велику нагороду. Винахідник запросив дати йому за першу клітину шахівниці одну пшеничну зернину, за другу – дві, за третю – чотири і далі за кожну клітину вдвічі більше, ніж за попередню. Цар здивувався, що винахідник так мало запросив. Але обіцянку не зміг виконати. Чому?
19. Знайти перший і останній члени геометричної прогресії, у якій b1=3, q=2, S8=765.
20. Між числами 9 і 243 написати два числа, які разом із даними числами утворюють геометричну прогресію.
21. Знайти перший член і знаменник геометричної прогресії, у якій b8-b1=15, b4-b2=6.
22. Знайти чотири числа, які утворюють геометричну прогресію, у якої сума крайніх членів дорівнює 49, а сума середніх членів дорівнює 14.
23. Добуток перших трьох членів геометричної прогресії дорівнює 1728, а сума їх дорівнює 63. Знайти перший член та знаменник цієї прогресії.