Показникова та логагифмічна функції

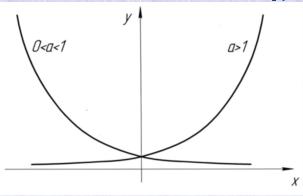
Основні властивості показникової функції y=a^x.
1. Область визначення функції a^x – множина R дійсних чисел.
2. Область значень функції a^x (якщо a≠1) – множина R₊ всіх додатних дійсних чисел. Якщо a=1, функція a^x при всіх x стала: вона дорівнює 1.
3. Якщо a>1, функція a^x зростає на всій числовій прямій; якщо 0<a<1, функція a^x спадає на множині R.

Основні властивості логарифмічної функції y=log_ax.
1. Область визначення логарифмічної функції – множина R₊ всіх додатних чисел.
2. Область значень логарифмічної функції – множина R всіх дійсних чисел.
3. Логарифмічна функція на всій області визначення R₊ зростає, якщо a>0 і спадає, якщо 0<a<1.

Властивості степенів
Для будь-яких x, y і додатних a і b справедливі рівності:
a⁰=1; a¹=1;
a^x·a^y=a^x+y; a^x:a^y=a^x-y;
(a^x)^y=a^xy; (ab)^x=a^xb^x;

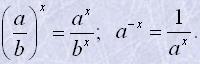
Властивості логарифмів
1. Якщо x>0, то
x=a^log_ax.
2. Логарифм основи дорівнює одиниці
log _aa=1.
3. Логарифм одиниці дорівнює нулю
log_a1=0 .
4. Якщо x₁>0 і x₂>0, то
log_a(x₁x₂)=log_ax₁+log_ax₂,

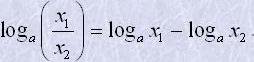
5. Якщо x>0, то log_ax^p=plog_ax,
де p – будь-яке дійсне число.
6. Якщо x>0, b>0, b≠1, то

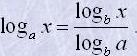
Зокрема,

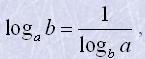
log_ab=log_a^pb^p=plog_a^pb

Показникові та логарифмічні рівняння
1. Показникове рівняння
a^f(x)=b^g(x) (a>0, a≠1, b>0, b≠1)
рівносильне рівнянню
f(x)log_ca=g(x)log_cb,
де c>0, c≠1.

2. Показникове рівняння
a^f(x)=a^g(x) (a>0, a≠1)
рівносильне рівнянню
f(x)=g(x).

Приклад 1
Розв’язати рівняння
1/4·4^x2=8·(0,5)^3x
Розв'язання
2^-2·(2²)^x2·(2^-1)^3x;
2^-2·2^2x2=2³·2^-3x;
2^-2+2x2=2^3-3x;
-2+2x²=3-3x;
2x²+3x-5=0;
x₁=1; x₂=-2,5.
Відповідь: x₁=1; x₂=-2,5.

Приклад 2
Розв’язати рівняння
3·4^x+2^x·3^x-2·9^x=0.
Розв'язання 3·(2^x)²+2^x·3^x-2·(3^x)²=0.
Це є однорідне рівняння. Поділимо ліву і праву частину рівняння на (3^x)².
3·((2/3)^x)²+(2/3)^x-2=0
Нехай (2/3)^x=t, тоді
3·t²+t-2=0;
t₁=2/3; t₂=-1<0 - стороній корінь
(2/3)^x=2/3;
x=1.
Відповідь: x=1.

3. Коренями рівняння
(u(x))^f(x)=(u(x))^g(x),
є розв'язки мішаної системи

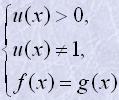
і ті значення x, для яких u(x)=1, якщо при цих значеннях визначені f(x) і g(x).

4. Логарифмічне рівняння
log_af(x)=b
рівносильне рівнянню
f(x)=a^b.

Приклад 3
Розв’язати рівняння log₂(x²+4x+3)=3.
Розв'язання
Задане рівняння рівносильне рівнянню
x²+4x+3=2³;
x²+4x+3=8;
x²+4x-5=0;
x₁=-5; x₂=1.
Відповідь: x₁=-5; x₂=1.

5. Логарифмічне рівняння
log_af(x)=log_ag(x)
рівносильне одній з таких систем

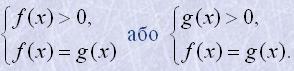
Приклад 4
Розв’язати рівняння log₃(x²-4x-5)=log₃(7-3x).
Розв'язання
Задане рівняння рівносильне системі

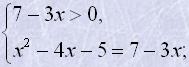
Область визначення рівняння:

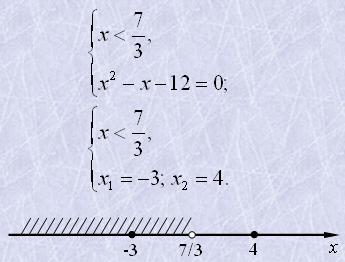
Відповідь: x₁=-3.

6. Для розв'язування рівнянь
log_af(x)+log_ag(x)=log_au(x),
log_af(x)-log_ag(x)=log_au(x),
plog_af(x)=log_au(x)
їх приводять до вигляду
log_a(f(x)g(x))=log_au(x),

log_af(x)^p=log_au(x).
Із знайдених коренів треба включити у відповідь ті, для яких f(x)>0, g(x)>0, u(x)>0.

Приклад 5
Розв’язати рівняння lg(x+3)-21lg(x-2)=lg0,4.
Розв'язання
Область визначення рівняння:

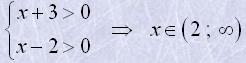
Застосовуючи властивості логарифмів, виконаємо деякі перетво-рення:
lg(x+3)=lg(x-2)²+lg0,4;
x+3=0,4(x-2)²; 0,4x²-2,6x-1,4=0; 2x²-13-7=0; x₁=7; x₂=-1/2. x₂=-1/2 - не входить до області визначення.
Відповідь: x=7.

7. Якщо при розв'язуванні рівняння застосовують перетворення виду loga(f(x)g(x)),

loga(f(x))p,

де p – парне число, то виникає небезпека втрати коренів заданого рівняння.
Щоб запобігти втраті коренів треба користуватись формулами у такому вигляді:
log_a(f(x)g(x))=log_a|f(x)|+log_a|g(x)|,

=loga|f(x)|-loga|g(x)|

log_a(f(x))^p=plog_a|f(x)|.

Показникові і логарифмічні нерівності

Показникова нерівність (exponential inequality) a^f(x)>a^g(x)
при a>1 рівносильна нерівності
f(x)>g(x), а при 0<a<1 – нерівності
f(x)<g(x).

Логарифмічна нерівність (logarithmic inequality) log_af(x)>log_ag(x)
при a>1 рівносильна системі нерівностей

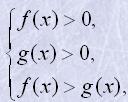
а при 0<a<1 – системі нерівностей


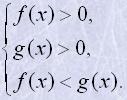
Приклад 6
Розв’язати нерівність
log_0,2(x²-x-2)>log_0,2(-x²+2x+3).
Розв'язання
Користуючись властивістю логарифмічної функції, отримаємо, що дана нерівність рівносильна системі нерівностей:

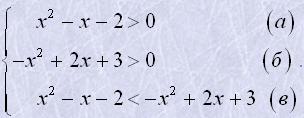
Розв’язуємо кожну нерівність системи:

а)	б)	в)
x2-x-2>0,	-x2+2x+3>0	x2-x-2>-x2+2x+3
x1=2, x2=-1	x2-2x-3<0	2x2-3x-5>0
	x1=-1, x2=3	x1=-1, x2=2,5
x∈(-∞;-1)∪(2;∞)	x∈(-1;3)	x∈(-∞;-1)∪(2,5;∞)

Знайдемо розв’язання системи:

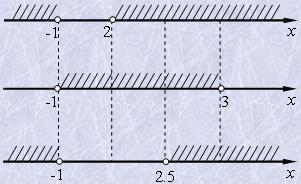
Відповідь: x∈(2,5;3).

Приклад 7

Розв’язати нерівність

(x-1)-log2(x-1)-2≤0

Розв'язання
Нехай log₂(x-1)=t,
t²-t-2≤0,


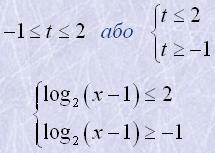
Дана система рівносильна такій системі:

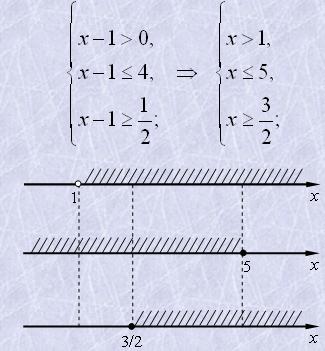
Відповідь: x∈[3/2;5].

Вправи

1. Знайти область визначення функції:

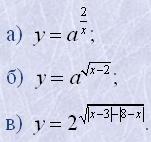
2. Перевірити рівності:

а) log39=2;	в) log5125=3;
б) lo416=2;

3. Знайти x, якщо:
а) xlog₂0,125=-2;

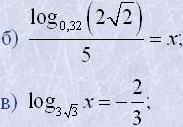
г) log₃(x-2)=2;

4. Обчислити:
а) 2log₅25+3log₂64;
б) log₂log₂16;
в) log₆36+5log₇49+4log_1/24.

5. Знайти x:
а) 2log₃x=3log₃x-2;
б) 5log₂x-3log₇49=2log₂x;
в) (log₃x)²-3log₃x+2=0;
г) (log₂x)²-log₂x-2=0;

6. Знайти область визначення функції:

а) y=log2(x2-1);	в) y=log3log0,5x.

7. Порівняти x і y:

а) log3x<log3y	в) logπx>logπy.
б) log0,1x<log0,1y;

8. Порівняти:

а) log89 чи log98;	в) log55 чи log66;
б) log41 чи log51;	г) log0,150,15 чи log22.

9. Обчислити:

а) 101-2lg10;

10. Знайти x:
a) lgx=lg7-lg3+lg2;

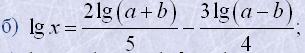
в) lgx=3lga+2lgb-4lgc.

11. Довести рівності:

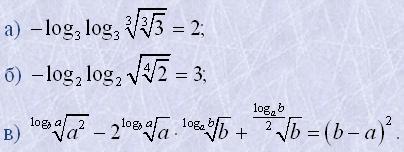
12. Обчислити A, якщо:

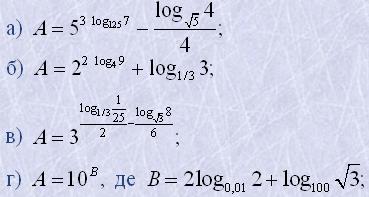
13. Знайти значення виразів:

а) 10lg12;

б) 101-lg2,5;

в) 0,1lg6-lg2.

14. Записати числа в стандартному вигляді (a·10ⁿ, де 1<a<10):
123; 14,36; 8500; 13750; 13,7; 3; 715; 19,14; 0,81; 0,305; 123000000; 0,00895; 0,0000001; 0,0007001.

15. Знайти значення виразів:

а) lg153-lg15,3;	в) lg0,08-lg272+lg3800.
б) lg14,24-lg85,44+lg60;

16. Розв'язати рівняння:

а) 3-x=81;	е) 2x-2=1;
б) 22x-1=8;	ж) 193x+x-2=1;
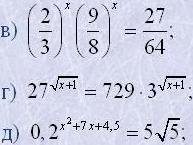	и) 3x+3x+1; к) 2x-1+2x-2+2x-3=448; л) 32x-3x=702;

17. Розв'язати рівняння:

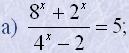
б) 12^x+27^x=2·8^x;

г) 27^x-13·9^x+13·3^x+1-27=0;


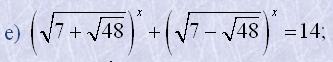
ж) (x-3)^3x2-10x+3=1;
и) |x-3|^3x2-10x+3=1;
к) (x-3)^x2-x=(x-3)².

18. Розв'язати системи рівнянь:

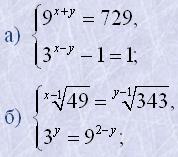
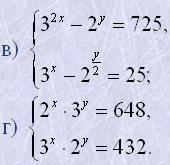
19. Розв'язати рівняння:
a) log₃x=2;

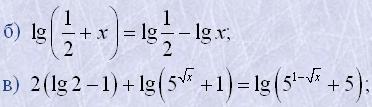
г) log₄log₂x+log₂log₄x=2;
д) log_4x+17+log_9x7=0;

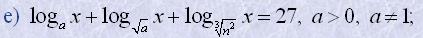
ж) log₂(4·3^x-6)-log₂(9^x-6)=1;

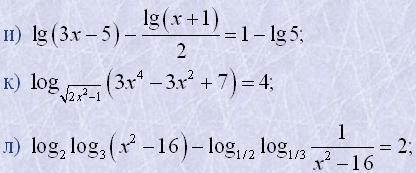
м) |log₂(3x-1)-log₂3|=|log₂(5-2x)-1|.

20. Розв'язати системи рівнянь:

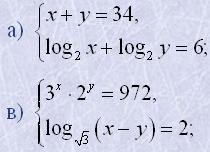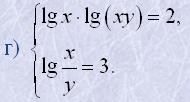21. Розв'язати нерівності:

а) 3x>81;	г) 0,32x2-3x+6<0,00243;
	д) 5·23x-24·25-3x+56≤0
в) 0,5x2-4x<8;	е) (x-3)x2-7x>1.

22. Розв'язати нерівності:

а) log2(3x+1)>log2(x-1);	д) log4(x+7)>log2(x+1);
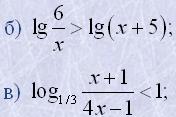г) log0,5(2x+3)≤log0,5(4x-1);
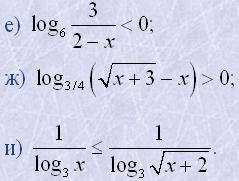