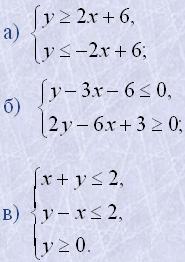Нерівності

Число a вважається більшим від b, якщо різниця a-b – число додатне; число a менше від b, якщо різниця a-b – число від'ємне.

Знаки (знак – sign) < і > називають знаками строгої нерівності (строга нерівнсть – strict inequality). Знаки ≤ і ≥ також протилежні один одному, їх називають знаками нестрогої нерівності (нестрога нерівність – unstrict inequality). Будь-який із знаків <, >, ≤ і ≥ називають знаком нерівності.
Два вирази, з'єднані знаком нерівності, утворюють нерівність.
Якщо обидві частини нерівності – числа, її називають числовою не-рівністю.

Властивості числових нерівностей
1. Якщо a<b і b<c, то a<c.
2. Якщо до обох частин правильної нерівності додати одне й те саме число, то дістанемо правильну нерівність.
3. Якщо обидві частини правильної нерівності помножити на одне й те саме додатне число, то дістанемо правильну нерівність. Якщо обидві частини правильної нерівності помножити на одне й те саме від'ємне число і змінити знак нерівності на протилежний, то дістанемо правильну нерівність.
4. Нерівності з однаковими знаками можна почленно додавати.
5. Нерівності з однаковими знаками можна почленно перемножати, якщо їх ліві і праві частини – додатні числа.

Розв'язування нерівностей з однією змінною
Розв'язком нерівності з однією змінною називається значення цієї змінної, яке задовольняє дану нерівність.
Розв'язати нерівність – це означає знайти всі її розв'язки або показати, що їх немає.
Розв'язують нерівність, замінюючи її іншими нерів¬ностями, прості-шими і рівносильними їй.
Дві нерівності називають рівносильними (рівносильні нерівності – equivalent inequalities), якщо вони мають одні й ті самі розв'язки, тобто якщо кожний розв’язок першої нерівності задовольняє другу, а кожний розв’язок другої нерівності задовольняє першу.

Властивості нерівностей із змінними
1. Якщо з однієї частини нерівності перенесемо в іншу доданок з протилежним знаком, то отримаємо нерівність рівносильну даній.
2. Якщо обидві частини нерівності помножимо або поділимо на одне й те саме додатне число, то отримаємо нерівність рівносильну даній.
3. Якщо обидві частини нерівності помножимо або поділимо на одне й те саме від'ємне число, змінивши при цьому знак нерівності на протилежний, то отримаємо нерівність рівносильну даній.

Нерівність виду

(замість знака > можуть бути знаки <, ≤, ≥, а функція в знаменнику може бути константою) розв'язується методом проміжків:

а) на числову вісь наносять точки x1, x2,...,xn, що розбивають її на проміжки, в яких вираз

зберігає знак.

Такими точками можуть бути корені рівнянь f(x)=0 і g(x)=0. Відповідні цим кореням точки позначають на числовій прямій: зафарбованими кружками – точки, які задовольняють дану нерівність, а незафарбованими – точки, які її не задовольняють.

б) знаходять і позначають на числовій осі знак виразу

для значень x, які належать кожному з проміжків.

Приклад 1

Розв'язати нерівність

Розв'язуємо рівняння
(x+3)(5-x)=0;
x₁=-3; x₂=5.
2x-5=0;
x₃=2,5.
Оскільки нерівність строга, то числа x₁=-3; x₂=5; x₃=2,5 не є розв'язками заданої нерівності, тому на числовій прямій їх позначаємо світлими кружками.

Ці точки розбивають числову вісь на чотири проміжки. На кожному проміжку визначаємо знак виразу

і проставляємо його на числовій прямій:

З отриманого рисунка отримаємо відповідь: x∈(-∞;-3)∪(2,5;5).

Ірраціональна нерівність (irrational inequality)

рівносильна системі нерівностей

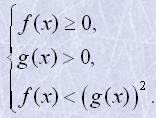
Ірраціональна нерівність

рівносильна сукупності систем нерівностей

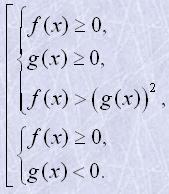
Система нерівностей (inequality system) Розв'язком системи нерівностей з однією змінною називають значення змінної, яке задовольняє кожну з нерівностей даної системи. Розв'язати систему нерівностей – це означає знайти всі її розв'язки або показати, що їх немає.

Приклад 2

Розв'язати нерівність

Розв'язання
Задана ірраціональна нерівність рівносильна системі:

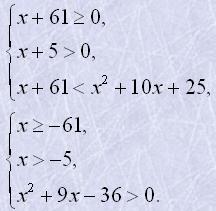
Розв'яжемо квадратне рівняння
x²+9x-36=0
x₁=-12, x₂=3.
Знаходимо розв'язок кожної нерівності на різних числових прямих, зберігаючи при цьому взаємне розташування точок:

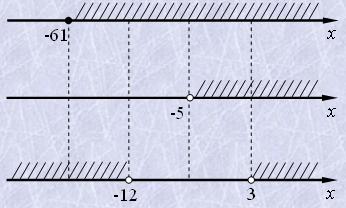
Розв'язки усіх нерівностей збігаються лише на проміжку x∈(3;∞). Відповідь: x∈(3;∞).

Вправи

1. Від першої нерівності відняти другу:
а) 6>3; 2<5;
б) -8<-5; -2>-7;
в) 2x>b²; a²<9-x;
г) 2a²>b; x²<9.

2. Помножити обидві частини нерівності на вказаний множник:
а) 5>-2 на 5;
б) -7<-5 на –2;
в) x-1>7 на a²+4;
г) x+2<c на -x²-4.

3. Розділити обидві частини нерівності на вказаний дільник:
а) -6<9 на 3;
б) -15>-35 на -5.

4. Чи рівносильні нерівності:

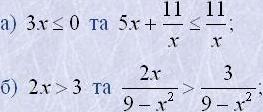
в) 2x+3>0 та 2x+3+(x-8)>x-8.

5. Розв'язати нерівності:
а) x+a>2-3x;

6. Розв'язати системи нерівностей

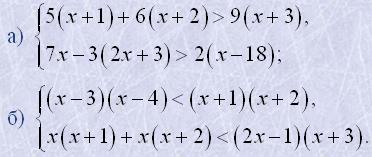
7. Розв'язати нерівності:

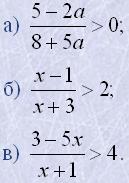
8. Знайти найбільше натуральне x, яке задовольняє систему нерівностей:

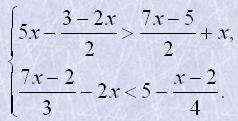
9. Розв'язати нерівності:
а) |x-3|>5;

в) |x+2|+|x|+|x-2|<4;

10. Довести нерівності:

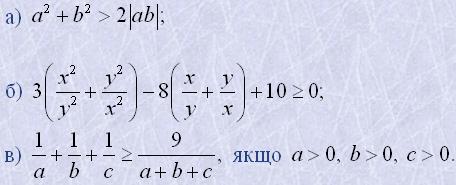
11. Розв'язати нерівності:

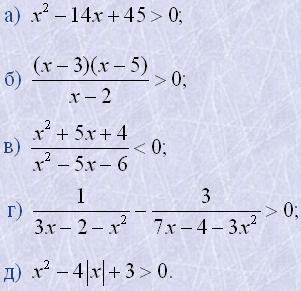
12. При яких значеннях m корені рівнянь будуть дійсними і різними:
а) x²+2(m-4)x+m²+6m=0;
б) (m+2)x²+(2m+3)x+m-1=0;
в) (5m+1)x²+(7m+3)x+3m=0.

13. Розв'язати нерівності:

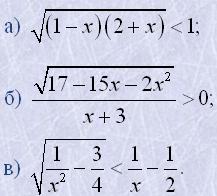
14. Розв'язати системи нерівностей:

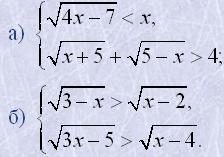
15. Розв'язати нерівності:
а) x+3y+1<0;
б) y≥6/x;
в) |y|≥x.

16. Розв'язати системи нерівностей: