Якщо кожному значенню змінної x з деякої множини (множина - set) D відповідає єдине значення змінної y, то таку відповідність називають функцією (функція - function).
При цьому x називають незалежною змінною (незалежна змінна - independent variable) або аргументом (аргумент - argument), y - залежною змінною (залежна змінна - dependent variable), а множину D - областю визначення даної функції.
Задають функції найчастіше формулами (формула - formula), таблично (таблиця - table) або графічно. Графіком функції називається множина всіх точок координатної площини, абсциси яких дорівнюють значенням аргументу, а ординати - відповідним значенням функції.
Наприклад, формула y=x2 задає функцію, яка виражає відповідність між числами і їх квадратами. Якщо область визначення цієї функції - множина цілих чисел з проміжку [-3;3], то її можна задати таблицею:
Графіком функції y=x2, заданої на множині всіх дійсних чисел R, є вся парабола (parabola) з нескінченними вітками (рис. 1). Область визначення цієї функції - множина R, а область значень - проміжок [0;+∞].
Елементарні функції
y=kx - пряма пропорційність (direct proportionality). Її графік - пряма, що проходить через початок координат (рис. 2).
Область визначення цієї функції - множина R, область значень, якщо k≠0 - теж множина R.
Лінійною (лінійна функція - linear function) називають функцію, яку можна задати формулою виду y=kx+b. Її графік - пряма, не паралельна (non-parallel) осі y (рис. 3). Область визначення R, область значень - множина R, якщо k≠0 .
Для побудови графіка лінійної функції досить знати координати двох його точок. Якщо k = 0, область значень - одне число b (рис. 4).
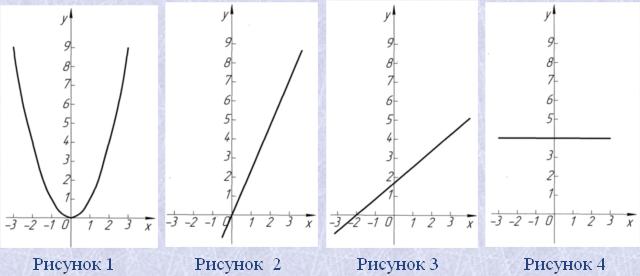
y=k/x – обернена пропорційність (inverse proportionality). Її графік – гіпербола (hyperbola). Коли k>0, вітки цієї гіперболи розміщені в І і ІІІ чвертях координатної площини (рис. 5), коли k<0 – в II и IV чвертях (рис. 6). Область визначення функції y=k/x множина R без числа 0, область значень – ця сама множина.
Графік функції y=x3 зображено на рис. 7. Її область визначення і множина значень – множина R.
| Графік функції | 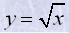 | – одна вітка параболи (рис. 8). Її область визначення [0;+∞) і область значень [0;+∞). |
Якщо змінна y залежить від x, то записують y=f(x). Символом f(a) позначають значення функції y=f(x) коли x=a. Нехай, наприклад, функцію задано формулою y=3x2-5. Можна записати і так: f(x)=3x2-5. У цьому випадку f(0)=3·02-5=-5; f(1)=3·12-5=-2; f(-2)=3·(-2)2-5=7 .
Зауваження. Якщо y=f(x), то часто кажуть, що y – функція від x, тобто функцією називають змінну y. Однак здебільшого під функцією розуміють не одну залежну змінну, а відповідність між значеннями двох змінних. До того ж – не будь-яку відповідність, а однозначну, при якій кожному значенню змінної х відповідає єдине значення змінної y.
Перетворення графіків елементарних функцій
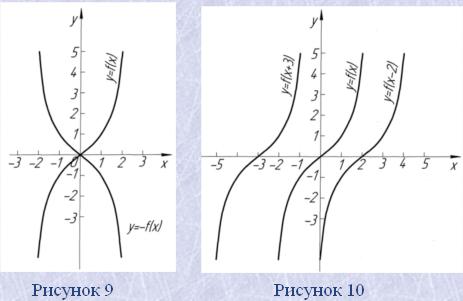
Графіки функцій y=f(x) і y=f(-x) симетричні відносно осі x (рис. 9).
Щоб побудувати графік функції y=kf(x), треба графік функції y=f(x) розтягнути від осі x в k разів, якщо k>1, або стиснути його в k разів до осі x, якщо 0Щоб отримати графік функції y=f(x)+n, треба графік функції y=f(x) перенести на n одиниць в напрямі осі y, якщо n>0 або в протилежному напрямі, якщо n<0.
Щоб отримати графік функції y=f(x-m), досить графік функції y=f(x) перенести на m одиниць в напрямі осі x, якщо m>0 або на -m одиниць в протилежному напрямі, якщо m<0 (рис. 10).
Функція, яка задається формулою y=ax2+bx+c, де a,b,c – довільні числа, а x – аргумент, називається квадратичною функцією.

| Графік функції y=ax2+bx+c – парабола, координати вершин якої | 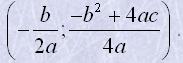 |
Якщо a>0, то вітки параболи направлені вверх, якщо a<0, то вітки параболи направлені вниз.
Щоб побудувати графік функції y=ax2+bx+c, можна знайти координати вершини параболи і ще кількох її точок, позначити їх на координатній площині і провести через них плавну лінію. Можна дотримуватись іншого способу: спочатку побудувати графік функції y=ax2+bx, а потім підняти або опустити його на |с| одиниць. Графік функції y=ax2+bx будувати неважко, оскільки він перетинає вісь абсцис у точках x=0 і x=-b/a, а її вершина знаходиться у
| точці | 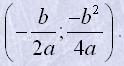 . . |
Описуючи властивості функції, звичайно починають з її області визначення. Область визначення функції (definitional domain) – проекція (projection) її графіка на вісь x; область значень функції (codomain) – проекція її графіка на вісь у (рис. 11).
Якщо для будь-яких двох значень аргумента більшому значенню аргумента відповідає більше значення функції, то таку функцію називають зростаючою (зростаюча функція – increasing function). Якщо для будь-яких двох значень аргумента більшому значенню аргумента відповідає менше значення функції, то таку функцію називають спадною (спадна функція – drop-down function). Наприклад, функції y=2x, y=x3 – зростаючі,
| а функції y=-2x, | 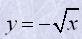 | – спадні. Графік зростаючої функції «іде вгору», а спадної – «опускається вниз». |
Можна також говорити про зростання чи спадання функції не на всій області визначення, а тільки на окремих проміжках.
Якщо графік функції симетричний (symmetric) відносно осі y, її називають парною (парна функція – even function). Якщо графік функції симетричний відносно початку координат, її називають непарною (непарна функція – odd function).
Функція y=f(x) парна, якщо її область визначення симетрична відносно нуля і для кожного значення x з області визначення f(-x)=f(x). Функція y=f(x) непарна, якщо її область визначення симетрична відносно нуля і для кожного значення x з області визначення -f(-x)=f(x).
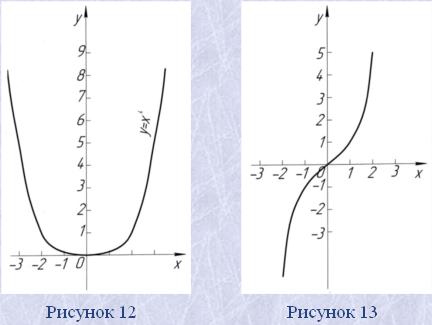
Функція, задана формулою y=xn, де x – аргумент, а n – довільне натуральне число, називається степеневою функцією (степенева функція – power function) з натуральним показником. Конкретні приклади таких функцій: y=x, y=x2, y=x3, …
Степенева функція з натуральним показником n парна, якщо число n парне (рис. 12) або непарна, якщо число n непарне (рис. 13).
Вправи
1. а) f(x)=2x2-3x+1. Знайти: f(0), f(3), f(-3).
| б) f(x)= | 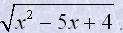 | Знайти: f(0), f(1), f(m+1). |
2. Знайти f(-1), f(1), f(0), f(3), якщо функція задана таблично
| x |
-4 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
| y |
17 |
5 |
2 |
1 |
2 |
5 |
10 |
17 |
3. Знайти f(-3), f(-2), f(0), f(2), f(5), f(8), f(2,75)
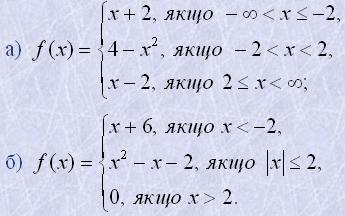
4. Записати однією формулою функції, використовуючи знак абсолютної величини:
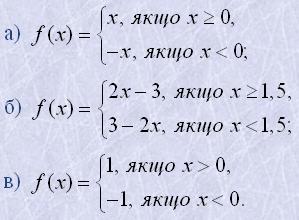
5. Знайти корені функції:
а) y=x-2;
б) y=x2-4;
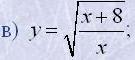
г) y=x2-2|x|-3.
6. Побудувати графіки функцій:
а) 3x-2y=0;
б) y=|x+1|-x+1.
7. Розв'язати графічно рівняння:
а) 5x+1=6;
б) |x|=1;
в) 2|x|-3=|x|+6.
8. Побудувати графіки функцій:
| 9. Чи належать графіку функції | 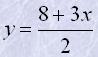 | дані точки: (2;7), (2;8), (3,9), (2/3;5), (1/3;4,5), (-2;1), (-1/2;5), (-2;-7). |
10. Знайти значення k якщо графік функції y=kx+2 проходить через точку P(-7;-12).
11. Розв'язати графічно системи рівнянь:
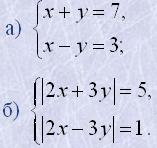
12. Побудувати графіки функцій:
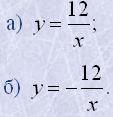
13. Розв'язати графічно системи рівнянь:
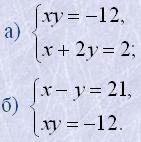

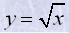




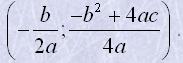
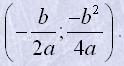 .
.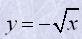

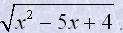
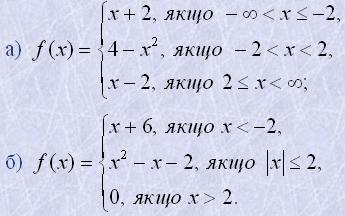
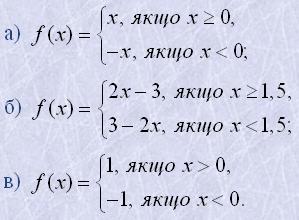
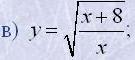
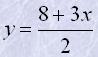
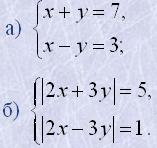
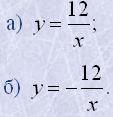
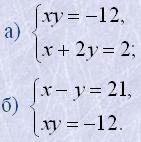
![]()
![]()
![]()