2.5 Інтервальні нечіткі множини в задачі кластеризації

Розв’язки задачі кластерного аналізу, отримані за допомогою методу можливісної кластеризації РСМ, більше відповідають дійсності та інтуїтивному уявленню про природу кластерів. Не зважаючи на таке вдосконалення, одна проблема залишається спільною для FCM та PCM: обидва методи в усіх обчисленнях спираються на параметр m, що задає рівень нечіткості кластерів.

Випадок m = 1 відповідає чіткій кластеризації. Зі зростанням m ступені належності всіх без винятку точок до всіх кластерів наближаються до 0,5, як показано на рис. 2.4 (для випадку двох кластерів). Кожна крива зображає зміну ступеня належності точки до одного з кластерів.

 

Рисунок 2.4 – Зміна ступенів належності точки до кластерів при зміні

рівня нечіткості:

              а) точка нерепрезентативна;

              б) точка репрезентативна.

 

На рис. 2.4 видно, що в усіх випадках m змінюється монотонно та не утворює локальних екстремумів. Тому закономірно, що строго обґрунтованих механізмів визначення m не існує. Існує ряд критеріїв якості (validity indices) кластеризації, пряме призначення яких – кількісна оцінка якості результатів кластеризації як поєднання умов подібності об’єктів у межах одного кластера та відмінності об’єктів із різних кластерів. Найбільш традиційне їх застосування – визначення оптимального числа кластерів, але можливо використовувати їх і для оцінки впливу інших параметрів. Наведемо найпоширеніші критерії якості.

Індекс розбиття (Partition Index):

 

 

де µ_ij – ступінь належності точки j до кластера і;

v_j - центр j-го кластеру;

m – рівень нечіткості;

с – кількість кластерів;

N – кількість точок.

Критерії Хіе-Бені та Квона беруть до уваги геометричні властивості кластерів, а не лише відстані об’єктів до їхніх центрів.

Критерій Квона:

 

 

де  - середнє значення центрів кластерів.

Критерій Хіе-Бені:

 

 

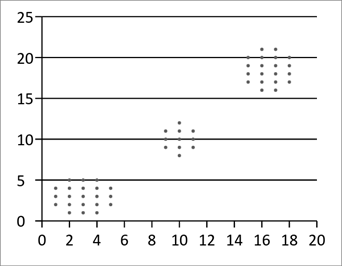
Менші значення наведених критеріїв відповідають кращим варіантам розбиття. Число кластерів вважатимемо вихідним параметром, заданим заздалегідь. Критерії ж якості пропонується використовувати для визначення оптимального значення рівня нечіткості. Дослідимо характер зміни їхніх значень залежно від зміни рівня нечіткості m на прикладі тестових наборів даних, зображених на рис. 2.5. Випадок 2.5 (б) відрізняється від 2.5 (а) наявністю аномальних об’єктів (шуму).

Розв’яжемо поставлену задачу методом РСМ при різних значеннях параметру m та обчислимо значення критеріїв якості за наведеними вище співвідношеннями. Для початкової ініціалізації центрів кластерів та ступенів належності будемо використовувати метод FCM Дж. Беждека.

 

   

                            а)                                                          б)

 

Рисунок 2.5 – Тестові набори даних:

                                    а) ідеальний (без аномальних спостережень)

                                    б) зашумлений (з аномальними спостереженнями)

 

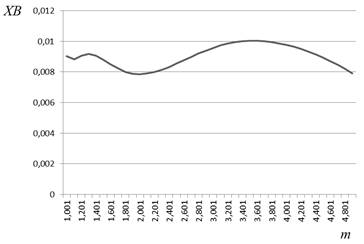
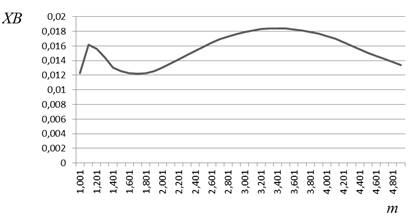
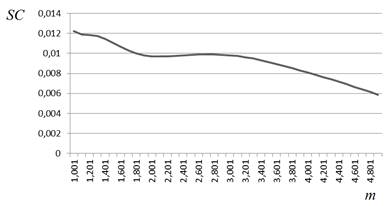
Залежності значення відповідного критерію від значення рівня нечіткості  m наведено на рис. 2.6.

 

   

                      а)                                                                б)       

                                  в)                                                              г)

                        д)                                                              е)

Рисунок 2.6 – Характер зміни значень критеріїв якості залежно від значення рівня нечіткості:

            а) критерій Квона, набір 1;

            б) критерій Квона, набір 2;

            в) критерій Хіе-Бені, набір 1;

            г) критерій Хіе-Бені, набір 2;

            д) індекс розбиття, набір 1;

            е) індекс розбиття, набір 2.

 

Випадки (а), (в) і (д) відповідно демонструють характер зміни значень критеріїв Квона, Хіе-Бені та індексу розбиття на наборі даних 2.5 (а), в якому відсутні аномальні спостереження. Випадки (б), (г) та (е) відповідають зашумленому набору даних 2.5 (б).

Якщо говорити про самі результати кластеризації (ступені належності точок до кластерів), то кожен із наведених критеріїв має глобальний або локальний мінімум, що відповідає рекомендованому значенню m. Прийнявши це значення за оптимальне, можна побудувати розв’язок, подібний до зображеного на рис. 2.7.

На рис. 2.7 (а) наведено розв’язок задачі кластеризації за значення m = 2, що відповідає мінімуму кривої зміни індексу Хіе-Бені на наборі даних 2.5 (а). Результати кластеризації представлено у вигляді нечітких множин: для кожного об’єкта на осі абсцис по осі ординат відкладено його ступені належності до кожного з кластерів. Набору даних 2.5 (б) відповідає розв’язок 2.7 (б). На рис. 2.7 (в) зображено класичні нечіткі множини типу 1.

 

 

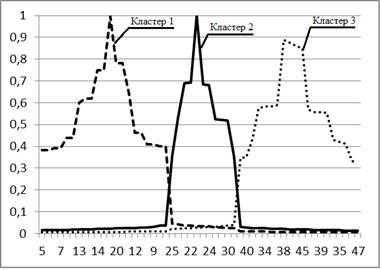
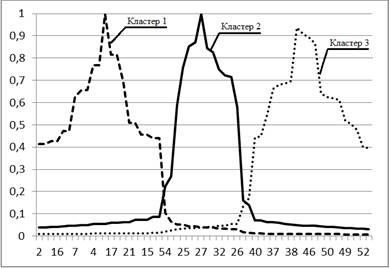
                      а)                                                              б)

 

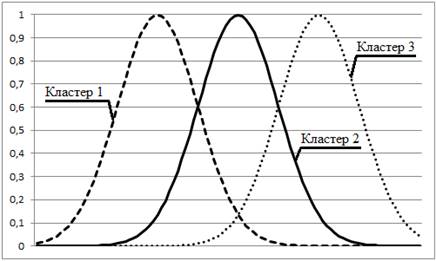
в)

 

Рисунок 2.7 – Результати кластеризації як нечіткі множини типу 1.

 

Отже, прийнявши значення рівня нечіткості m = 2, ми отримали деякий розв’язок задачі кластеризації для заданого набору даних. Але, проаналізувавши криві 2.6 а – е, можна помітити, що вони мають мінімуми за різних значень m. Так, окрім уже згаданого m = 2 у випадку 2.6 (в), маємо результати m = 1,9 для 2.6 (а), m = 2,1 для 2.6 (д), m = 1,7 для 2.6 (б) та (г), m = 1,6 для 2.6 (е). Таким чином, залежно від способу розв’язання задачі (критерію якості) та якості вхідних даних (наявності чи відсутності аномалій) нами отримано п’ять варіантів розв’язку, кожен із яких претендує на оптимальність. Шостим претендентом можна вважати значення m = 1,5, рекомендоване для даної задачі. Остаточно визначити, який із розв’язків-претендентів є вірним, і чи є серед них вірний розв’язок, не видається можливим. Тому для того, щоб убезпечити себе від помилкового результату, пов’язаного з неправильним вибором значення m, доцільно використовувати інтервальні ступені належності.

Рівень нечіткості m, як правило, задається емпірично дослідником, при цьому доводиться повністю покладатися на це заздалегідь задане значення без жодних гарантій його правильності. З цим пов’язана невизначеність, яку неможливо врахувати, коли отримане значення міри належності точки до кластера являє собою єдине число. Тому для того, щоб убезпечити себе від помилкового результату, пов’язаного з неправильним вибором значення m, доцільно використовувати інтервальні функції належності типу 2. Такий підхід найчастіше застосовується тоді, коли точний характер розподілу ступенів належності другого типу в області між границями інтервалу невідомий. Саме такий випадок являє собою задача кластеризації: невідомо, чи піддається виділенню та математичному опису закономірність, за якою розподілені ступені належності другого типу, та чи має дослідження цієї закономірності практичний сенс. З іншого боку, інформація про верхню та нижню функції належності, що описують кожен кластер залежно від значення параметру m, має виняткову цінність, оскільки інтервал (його ширина та розташування відносно нуля та одиниці) несе значно більше інформації про міру належності точки до кластера, ніж єдине число. Наприклад, ширина інтервалу може свідчити про ступінь достовірності отриманого розв’язку. Тому пропонується модифікувати алгоритм можливісної кластеризації РСМ для роботи з інтервальними ступенями належності. Цим буде досягнуто повне врахування невизначеності, пов’язаної з різними можливими значеннями рівня нечіткості, для подальшого аналізу результатів кластеризації.

Адаптуємо метод для роботи з інтервальними ступенями належності точок до кластерів. В основі пропонованого методу лежить алгоритм кластеризації PCM. Окрім нетрадиційного трактування ступенів належності та стійкості до шуму він володіє ще однією властивістю. Йдеться про те, що, оскільки міри належності однієї й тієї самої точки до різних кластерів незалежні одна від одної, ступінь належності точки до одного з них можна змінити без обов’язкової процедури перерахунку ступенів її належності до всіх інших кластерів. Дана властивість є надзвичайно корисною, оскільки вона дає змогу «розтягти» ступінь належності точки до кластера з чіткого значення в інтервал, і це не ставить під загрозу виконання обмеження на суму значень ступенів належності точки до всіх наявних кластерів.

Отже, виходячи з визначення ступеня належності як міри типовості заданої точки для відповідного кластеру, знайдемо такі значення невідомих параметрів, які ведуть до мінімуму функціоналу (1.2). Враховуючи властивості рівня нечіткості m та його вплив на результати кластерного аналізу, необхідно подати ступені належності у вигляді інтервалів, ліва та права границі яких лежать у межах [0, 1].

Для визначення меж інтервалу розтягу ступеня належності скористаємося критеріями кластеризації. Перший локальний мінімум критеріїв K, SC та XB відповідає оптимальному значенню m, тому за межі інтервалу зміни рівня нечіткості приймемо точки перегину кривих 2.6 (а) та (б) по обидва боки від цієї точки. Тоді ступінь належності точки до кожного з кластерів буде лежати в межах [µ_ijL, µ_ijU], де границями інтервалу є відповідні значення µ_ij у згаданих точках перегину.

Для початкової ініціалізації центрів кластерів використаємо звичайний метод FCM. Він збігається за лічені ітерації, тому якнайкраще підходить для цього завдання, адже воно вимагає грубого наближеного розв’язку.

 Виходячи з усього сказаного вище, можна сформулювати покроковий алгоритм розв’язання задачі кластерного аналізу.

1. Глобальні значення критеріїв якості ініціалізувати максимально можливим значенням.
2. Визначити приблизні місця розташування центрів кластерів за допомогою алгоритму FCM.
3. Оцінити значення η для результату роботи FCM.
4. Сформувати матрицю D як матрицю Евклідових відстаней від кожної точки з вихідної множини до центру кожного з кластерів.
5. Задати початкове значення рівня нечіткості m = 1.
6. Розрахувати початкове значення локальних критеріїв якості.
7. Розрахувати функцію належності для кожної з пар (точка, кластер), користуючись відповідним співвідношенням із методу РСМ.
8. Перерахувати положення центрів кластерів за формулою, спільною для обох методів.
9.  Перерахувати матрицю відстаней D.
10.  Розрахувати цільову функцію РСМ при заданих значеннях ступенів належності, координат центрів кластерів, елементів матриці D та вектора η.
11.  Якщо розраховане значення цільової функції менше за отримане на попередній ітерації, повернутись до кроку 8.
12.  Розрахувати значення локальних критеріїв якості при заданому m. Знаючи поточне значення критерію та його значення з попередньої ітерації, визначити, чи є попереднє значення локальним екстремумом. Якщо так, зберегти попереднє значення m, характер екстремуму відповідного критерію в цій точці та побудоване розбиття (центри кластерів і ступені належності).
13.  Перерахувати значення глобальних критеріїв якості.
14.   Серед усіх проміжних результатів вибрати три значення m, за яких глобальні критерії досягають мінімального значення. Для кожного з них серед збережених на кроці 13 екстремальних точок вибрати найближчі справа та зліва. Побудувати інтервали зміни значень рівня нечіткості за кожним критерієм:  та .
15. Об’єднати інтервали рівня нечіткості за правилом

(3.6)

 

         Інтервали зміни рівня нечіткості, отримані після кроку 16 для кожного з критеріїв якості, можна використовувати напряму для розрахунку ступенів належності. Тоді отримаємо кластери у вигляді інтервальних нечітких множин, як показано на рис. 2.8 для критерію Квона. Випадок (а) відповідає набору 2.5 (а), випадок (б) – набору 2.5 (б).

 

  

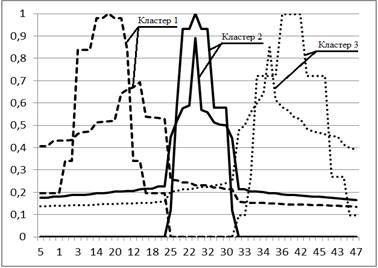
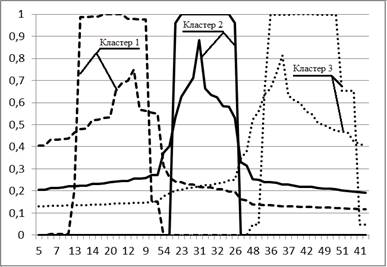
                        a)                                                                    б)

 

Рисунок 2.8 – Результати інтервальної нечіткої кластеризації на основі критерію Квона

 

Ширина інтервалу рівня нечіткості відображається також на значення ступенів належності. Хоча в результатах у цілому прослідковується тенденція до утворення компактних кластерів, деякі об’єкти мають значну невизначеність у ступенях належності. Серед таких об’єктів, наприклад, точка 20 (μ_20,2 = [0,52; 0,98]). Ця невизначеність є природною особливістю, характерною для будь-якої емпіричної оцінки.

Аномальні спостереження, присутні в наборі 2.5 (б), також вносять невизначеність у результати кластеризації. Але найбільшим недоліком цього методу є те, що сам критерій якості, що використовується, вносить певну невизначеність у результати та генерує ступені належності з широким інтервалом навіть для «чистого» набору даних, апріорі вільного від аномальних спостережень. Про це свідчать розбіжності оцінок, отриманих за допомогою різних критеріїв.

Для того, щоб зменшити вплив внутрішніх особливостей одного конкретного критерію якості на кінцевий результат, до формування інтервалу залучаються інші критерії. В постановці задачі кластерного аналізу як задачі навчання без учителя єдино вірний розв’язок завжди невідомий, тому для гарантованого попадання вірного розв’язку в остаточний інтервал необхідно виконувати об’єднання інтервалів, отриманих за критеріями Квона, Хіе-Бені та індексом розбиття.

Так, у наведеному тестовому прикладі для набору 2.5 (а)

Для набору 2.5 (б):

Інтервальні нечіткі кластери, отримані за таких значень рівня нечіткості, наведено на рис. 2.9.

 

     

                                a)                                                                б)

 

Рисунок 2.9 – Результати інтервальної нечіткої кластеризації на основі комбінації критеріїв Квона, Хіе-Бені та індексу розбиття.

 

Таким чином, скомбінувавши три критерії якості та визначивши область об’єднання інтервалів, отриманих за кожним із них, бачимо, що значення рівня нечіткості для зашумлених даних набору 2.5 (б) знаходяться приблизно в тому ж інтервалі, що й для позбавленого аномалій набору даних 2.5 (а), що ще раз підтверджує незалежність результатів роботи методу від наявності в аналізованому наборі даних шумів та аномалій.

Отже, інтервальні ступені належності дають змогу враховувати та моделювати невизначеності, пов’язані з браком експертних знань, характерним для моделей на основі навчання без учителя, таких як кластерний аналіз.