1 Нечіткі множини типу 1

1.1  Основні відомості. Операції над нечіткими множинами типу 1

Завданням нечітких множин є визначення належності деякого об'єкта чи елемента до заданої множини. Нехай Е – деяка множина, а А – підмножина Е, тобто . Той факт, що елемент x множини Е належить і множині А в теорії множин позначають так: . Щоб виразити цю належність, можна скористатися й іншим поняттям – характеристичною функцією μ_A(x), значення якої вказують, чи є (так або ні) х елементом А:

 

 

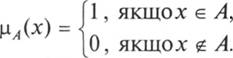
Згідно з теорією нечітких множин, характеристична функція належності може набувати будь-якого значення в інтервалі [0, 1], а не тільки два – 0 або 1. Відповідно до цього, елемент х_i множини Е може не належати А (μ_Α (х) = 0), бути елементом А невеликою мірою (значення μ_A(x) близьке до нуля), бути елементом А значною мірою (μ_A(x) близьке до 1) або бути елементом А (μ_A(x)=1). Отже, поняття належності узагальнюється. Нечітку підмножину А універсальної множини Е позначають А_н і визначають упорядкованими парами:

 

 

Характеристична функція належності (або просто функція належності) μ_A(x) набуває значень у деякій упорядкованій множині М (наприклад, 
М = [0, 1]). Ця функція належності вказує ступінь (або рівень) належності елемента х до підмножини А. Множину М називають множиною належностей. Якщо М = {0, 1}, то нечітку підмножину А можна розглядати як звичайну або чітку множину, функція належності якої набуває лише бінарних значень.

Тому основні операції над нечіткими множинами також являють собою узагальнення відповідних властивостей та операцій класичної теорії множин.

Рівність. Дві нечіткі множини  і , що задані на U, є рівними, якщо вони складаються з одних і тих же елементів для всіх  та . Позначаються як  =

Доповнення. Дві нечіткі множини  і , доповнюють одна одну, якщо  для всіх

Перетин. Перетином двох нечітких множин  і  є така множина , що складається з елементів для всіх  що одночасно належать  і  з функцією належності .

Об’єднання. Об’єднанням двох нечітких множин  і  є така множина , що складається з елементів для всіх  що належать  або  з функцією належності .

Різниця. Різницею двох нечітких множин  і  є така множина , що складається з елементів для всіх  що мають функцію належності , якщо , інакше .

На рис. 1.1 графічно показано основні операції над нечіткими множинами: а) , б) , в) , г) .

 

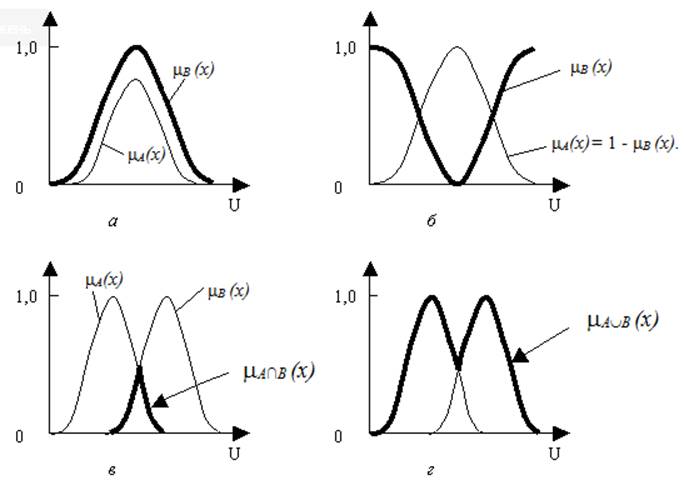
Рисунок 1.1 – Операції над нечіткими множинами

 

Декартовим добутком  двох нечітких множин  і , визначених відповідно на універсумах U₁ та U₂, є нечітка множина  пар (кортежів), визначених на U₁ та U₂ з функцією належності . Тобто =.

Види функцій належності. Існує багато кривих для визначення функцій належності. Найбільш розповсюдженими функціями належності є трикутна, трапецієвидна,  функція  Гаусса  та  Z- (або S-) подібні.

Трикутна функція належності визначається трійкою чисел (а, b, c), а її  значення в довільній точці х обчислюється за  формулою

 

 

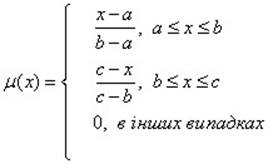
При (b-a)=(c-b) маємо симетричну трикутну функцію належності, яка однозначно задається  двома параметрами з трійки  (а, b, c).

Для визначення трапецієвидної функції належності потрібні чотири числа (a, b, c, d), а її  значення в заданій точці х обчислюється  за  формулою

 

 

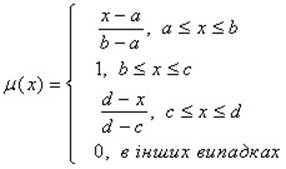
При (b-a)=(d-c) ця функція належності приймає симетричний вигляд.

Функція належності Гауса (рис. 1.2), зазвичай описується формулою 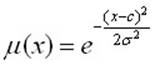та  визначається  параметрами (с, ).

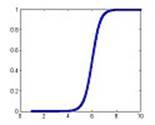
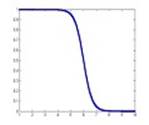
Z- та S-подібні функції належності одержали свою назву в зв’язку з виглядом  кривих, які зображують  їхні  графіки (рис. 1.3).

 

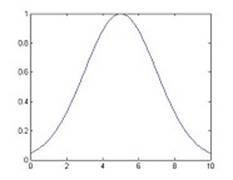
Рисунок 1.2 – Графік функції належності Гауса  при   с=5,  =2

 

                                                 

а)

б)

Рисунок 1.3 - Графіки сигмоїдальної функції належності при
(а) a=3, b=6; (б) a=-3, b=6

 

До типу Z- і  S-подібних функцій належить  сигмоїдальна функція належності, яка в загальному випадку описується формулою , де a, b – деякі числові параметри, такі, що a < b. При цьому, якщо а > 0, маємо S-подібну функцію належності, якщо a < 0 – Z-подібну.