1.3  Методи побудови нечітких логічних систем типу 1

Мендель та Ванг [18] виділяють 3 основні підходи до синтезу нечітких логічних систем та побудови нечітних баз знань.

1. Архітектура нечіткої моделі встановлюється дослідником, експериментальні дані використовуються лише для оптимізації параметрів. Такі властивості моделі як форма функцій належності, метод фазифікації та дефазифікації, t-норма, метод побудови нечіткого логічного висновку, кількість правил, кількість антецедентів (і в загальному випадку консеквентів) правила задає розробник моделі. При цьому невідомі величини, тобто параметри моделі, оптимізуються шляхом навчання на експериментальних даних. Емпіричний підхід до задання форми функцій належності та оптимального числа правил не завжди коректний, звідси висока ймовірність отримати логічно прозору модель, яка тим не менш недостатньо адекватно відображає досліджуваний процес.

2. Центри нечітких множин термів лінгвістичних змінних визначаються експериментальними даними. Решту параметрів нечітких множин задає розробник моделі. Правила будуються виключно на основі експериментальних даних, при цьому число нечітких множин термів кожної вхідної та вихідної змінної строго дорівнює числу правил та числу навчальних векторів даних. Отримана таким чином база правил надлишкова навіть для моделей невеликої розмірності; що стосується розв’язання задач вищої розмірності, то обсяг бази правил, побудованої за таким підходом, суттєво ускладнює обчислення. Цей підхід вимагає застосування додаткових методів зменшення надлишковості бази правил.

3. Нечіткі множини термів лінгвістичних змінних початково визначаються розробником; в подальшому з цими нечіткими множинами пов’язуються експериментальні дані (власне метод Менделя-Ванга, якому присвячено роботу). Цей підхід дозволяє зберегти розмірність бази знань в розумних межах за рахунок безпосередньої участі розробника в процесі формування нечітких множин кожного антецедента та консеквента. База правил в цьому підході містить число правил, менше або рівне числу навчальних векторів даних. При цьому модель від самого початку адекватна предметній галузі, оскільки побудована на експериментальни даних, отриманих в процесі функціонування реальної системи.

В залежності від вибраного підходу до синтезу нечіткої моделі дослідники схильні обирати ті чи інші методи побудови функцій належності нечітких змінних. Для першого підходу найбільш очевидним є прямий метод побудови функцій належності, який полягає в тому, що експерт безпосередньо задає правила визначення значень функції належності, що характеризує дане поняття. Ці значення узгоджуються з його уявленнями на множины об’єктів U таким чином:

1. Для будь-яких  тоді і тільки тоді, якщо  має перевагу над , тобто більшою мірою характеризується поняттям A.

2. Для будь-яких  тоді і тільки тоді, якщо  та  однаковою мірою характеризуються поняттям A.

Експерт може безпосередньо задавати значення функції належності таблицею, формулою, перерахуванням.

Очевидно, що такий спосіб задання функцій належності вимагає від експерта не лише знання предметної галузі, а й фундаментальних математичних знань. Для спрощення роботи експерта існує ряд непрямих методів, у яких значення функції належності вибираються таким чином, щоб задовільняти заздалегідь сформульованим умовам. Експертна інформація є лише вихідними даними для подальшої обробки.

Так, окрему групу складають методи на основі парних порівнянь, які полягають в обробці матриці оцінок, що відображає думку експерта про відносну належність елементів множині або ступеня вираженості в них властивості, що формалізується множиною [3]. Ступінь належності елементів множині визначається за допомогою оцінок, наведених в таблиці 1.1.

Таблиця 1.1

Шкала для визначення матриці суджень

Кожен із експертів заповнює матрицю парних порівнянь розміром NxN, де N – кількість альтернатив; для кожної пари альтернатив експерт вказує, яка з альтернатив має більшу перевагу (є кращою, важливішою тощо.) Існує ряд алгоритмів, що реалізують метод парних порівнять. Вони розрізняються за кількістю експертних оцінок, що використовуються (індивідуальті та колективні оцінки), за шкалами порівняння альтернатив та деякими іншими особливостями.

Найбільш широке розповсюдження з методів цієї групи на сьогоднішній день має метод аналізу ієрархій  (Analytic Hierarchy Process, AHP). Його особливість у відсутності обмеження на суму вагових коефіцієнтів, а отже і необхідності тримати в полі зору всі фактори (ознаки), присутні в системі, при роботі з кожним окремим фактором. Ідея методу полягає в структуризації задачі прийняття рішення шляхом побудови багаторівневої ієрархії, що об’єднує всі альтернативи, що існують в даній задачі. Альтернативи далі порівнюються між собою за допомогою того чи іншого різновиду процедури парних порівнянь. В результаті стає можливим отримання кількісних оцінок інтенсивності взаємовпливу елементів ієрархії, на основі яких оцінюється міра переваги альтернатив відносно цільового критерію задачі.

В результаті вдається отримати детальне уявлення про те, як саме взаємодіють фактори, що впливають на пріоритети альтернативних розв’язків, а також власне розв’язки. На противагу цьому, формування структури моделі прийняття рішення в методі AHD  - досить трудомісткий процес. Шкали суджень, що використовуються для визначення ваг альтернатив, в більшості своїй не дозволяють адекватно відобразити всі можливі відношення між альтернативами, та фактично працюють коректно лише на якісних показниках, без уточнення кількісних мір переваги однієї альтернативи над іншою. Крім того, метод АНР не враховує невизначеностей, пов’язаних із поданням судження у вигляді числа; з іншого боку, суб’єктивний характер суджень експертів має суттєвий вплив на отримані результати. Що стосується його потенційних застосувань для моделювання природних процесів,  часто неможливо зрозуміти, як саме взаємодіють фактори, та вибудувати семантично адекватну ієрархію ознак, адже далеко не всі реальні природні об’єкти і явища характеризуються набором ознак, який можна розбити на змістовні групи приблизно однакової потужності. З огляду на це, на сьогоднішній день метод AHP використовується переважно в задачі чіткого прийняття рішень за припущення повної відсутності невизначеностей в досліджуваній системі.

У методах побудови функцій належності лінгвістичних термів з використанням статистичних даних за ступінь належності елемента множині приймається оцінка частоти використання поняття, що задається нечіткою множиною, для характеристики елемента. Припустимо, що спостерігаючи за об’єктом протягом деякого часу, людина n разів фіксує свою увагу на тому, має місце факт А чи ні. Подія, що полягає в n перевірках наявності факту А, називаються оціночною. Нехай у k перевірках мав місце факт А. Тоді оператор реєструє частоту p=k/n появи факту А та оцінює її за допомогою лінгвістичних висловлювань на зразок «часто», «рідко» тощо.

Для обробки таких статистичних даних можна послуговуватись так званою матрицею підказок. Це та застосування методів апроксимації дозволяють отримати гладкі функції належності. Слід відзначити, що для коректної роботи методів цього класу вибірка спостережень відповідної події повинна мати достатню статистичну значущість.

При побудові функцій належності на основі експертних оцінок використовуються результати експертного опитування для синтезу наближених точкових (наприклад, X ПРИБЛИЗНО ДОРІВНЮЄ Y) або інтервальних (X ЗНАХОДИТЬСЯ ПРИБЛИЗНО В ІНТЕРВАЛІ ВІД Y ДО Z).

Для побудови нечіткого числа, приблизно рівного деякому числу K, можна використовувати функцію

                                                                                                        (1.1)

де  залежить від потрібного ступеня нечіткості  та визначається з виразу

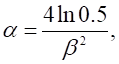
 - відстань між точками переходу для , тобто точками a і b, в яких функція вигляду (1.1) приймає значення 0.5.

Для визначення множини вигляду ЧИСЛО, ПРИБЛИЗНО РІВНЕ K, слід виявити, як експерти уявляють собі границі класів таких чисел. Для цього іноді проводяться статистичні дослідження. Опитуваним пропонують назвати такі a(K) та b(K), які на їхню думку відділяють числа, приблизно рівні K, від чисел, що такими не є. Таким чином, задача побудови  для деякого числа зводиться до відшукання параметрів a і b, щоб потім можна було визначити , за допомогою  - , та використовуючи , побудувати .

Параметричний підхід до побудови функцій належності полягає в побудові модифікованих нечітких термів на основі існуючих. При цьому визначаються параметри дробово-лінійного перетворення, що відповідає нечіткому модифікатору, та з його допомогою перетворюється вихідний терм. Метод базується на припущенні, що експерт, характеризуючи лінгвістичне значення деякої ознаки, з мінімальним зусиллям може вказати три точки універсальної шкали: A, B, C, з яких B та C – точки, які, на його думку, ще (або вже) не належать описуваному лінгвістичному значенню, А – точка, що беззаперечно йому належить.

Побудова функцій належності на основі інтервальних оцінок спирається на припущення, що експерт може вказати інтервал  значень критерію h, що відповідає побажанню вибрати, скажімо, «хороший» об’єкт. При цьому граничні значення інтервалу мають таку інтерпретацію. Нехай - результат вимірювання значення характеристики h для об’єкта а. Тоді  є границею «ідеальної» області, тобто якщо , об’єкт слід вважати таким, що ідеально відповідає поняттю «хороший». Можливість (з точки зору теорії можливостей) такого твердження  (Q – суб’єктивна подія, яка полягає в тому, що об’єкт, з точки зору експерта, знаходиться в стані «хороший».) Якщо , ситуація інтерпретується так: можливість того, що об’єкт а – «хороший», . Очевидно, що при  відповідні можливості мають значення .

Відчуття експерта про характер зміни ступеня відповідності об’єкта а поняттю «хороший» з наближенням значення  до границі , та апроксимуючи дані оцінок експертів для  та  ще в кілької точках z, отримують аналітичні вирази двох функцій  та , які називаються рівневими обмеженнями. Ці функції шляхом експертного опитування можна побудувати таким чином, щоб охопити весь діапазон реальної зміни параметра Z.

Для отримання повного уявлення про альтернативу а необхідно провести ряд експериментів із визначення оцінки  за різних значень z. За допомогою апроксимації отримують функцію ; для ряду значень z розраховуються значення , апроксимуючи які отримують ступінь відповідності альтернативи поняттю експерта «хороша альтернатива» на множині значень параметра Z. Отримана функція називається розподілом можливостей і являє собою нечітке обмеження на значеннях параметра Z.

Всі ці методи тим чи іншим чином використовуються в рамках першого з трьох підходів, визначених на початку цього огляду. Проте робота експерта з підготовки до прийняття рішень часто вимагає завеликих затрат часу для однієї людини та вимагає спеціальної математичної підготовки, що суттєво звужує коло потенційних фахівців, яких можна залучити до розробки моделі. Крім того, в межах цього підходу всі компоненти системи цілковито залежать від суджень експерта, які незалежно від його кваліфікації можуть розходитись із фактичними спостереженнями об’єктів реального світу.

Тому зважаючи на це та на очевидні недоліки другого підходу (надлишковість формату правил та бази знань), за наявності достатніх експериментальних даних надають перевагу третьому підходу до побудови нечітких моделей, який наряду з урахуванням експертних знань дозволяє побудову правил на основі об’єктивних даних функціонування реальної системи.