1.5 Нечіткі множини в задачах інтелектуального аналізу даних

Data Mining. Методи кластеризації

Задачі прийняття рішень в умовах невизначеності вимагають роботи з великими масивами багатовимірних даних, а тому тісно пов’язані з колом задач Data Mining, інтелектуального аналізу даних. Data Mining – це процес аналізу даних із різних точок зору та подання їх у вигляді корисної інформації, тобто такої, яку можна безпосередньо використовувати для розв’язання конкретних, зокрема оптимізаційних, задач. Технічно Data Mining – це процес виявлення кореляцій, зв’язків чи закономірностей в масштабах десятків полів у великих реляційних базах даних.

Математичний інструментарій методів Data Mining складають методи класифікації, моделювання, прогнозування, що ґрунтуються на використанні штучних нейронних мереж, генетичних алгоритмів, еволюційного програмування, асоціативної пам’яті, нечіткої логіки. Одним із призначень Data Mining також є наочне подання (візуалізація) результатів обчислень, що дозволяє використовувати технології Data Mining людьми, що не мають спеціальної математичної підготовки.

Задача Data Mining ставиться таким чином. Нехай є деяка досить велика база даних, та висувається припущення, що в базі даних знаходяться деякі «приховані знання». Необхідно розробити методи виявлення знань, прихованих у великому обсязі «сирих» даних. Знайдені закономірності в контексті загальної орієнтації сучасного програмного забезпечення на використання концепції Big Data можуть стати джерелом додаткових прибутків чи конкурентних переваг для компаній. «Приховані знання» повинні володіти рядом ознак. Це повинні бути знання

• раніше невідомі, нові;
• нетривіальні (такі, що їх не можна отримати будь-яким іншим простішим шляхом, наприклад, при безпосередньому візуальному аналізі даних або обчисленні простих статистичних характеристик);
• практично корисні, тобто такі, що мають цінність для дослідника чи споживача;
• доступні для інтерпретації, тобто знання, які легко можна подати в наочній для користувача формі та легко пояснити в термінах предметної галузі.

Знання, що добуваються за допомогою методів Data Mining, прийнято подавати у вигляді закономірностей, в ролі яких можуть виступати асоціативні правила, дерева розв’язків, кластери, математичні функції тощо.

Одним із найпотужніших інструментів Data Mining є кластерний аналіз. Він широко використовується для виділення прихованих закономірностей та внутрішніх взаємозв’язків у великих масивах багатовимірних даних. 

За допомогою кластеризації успішно розв’язуються задачі обробки та сегментації зображень, зокрема медичних, розпізнавання образів, розпізнавання та впорядкування мультимедійного трафіку, обробки та категоризації документів, сегментації множини абонентів провайдера телекомунікаційних послуг, будуються соціальні дослідження, економічні прогнози тощо. Кластерний аналіз також може використовуватись для виділення інформативних ознак при роботі з надлишковими даними.

Застосування методів кластерного аналізу дозволяє розв’язувати задачу класифікації об’єктів у випадку відсутності будь-якої інформації про кількісний або якісний склад кластерів.

В загальному вигляді алгоритм кластеризації – це функція a: X → Y, яка будь-якому об'єкту xX ставить у відповідність мітку кластера yY. Множина міток Y у деяких випадках відома заздалегідь, однак частіше ставиться завдання визначити оптимальне число кластерів з погляду того або іншого критерію якості кластеризації [5]. Для розв’язання цієї задачі універсальних методів, що дозволяють швидко знайти абсолютно точні розв’язки, не існує. Розв’язання задачі кластеризації принципово неоднозначне з декількох причин [7]. По-перше, не існує однозначно найкращого критерію якості кластеризації. Відомий ряд критеріїв та алгоритмів, що не мають чітко вираженого критерію, але які здійснюють досить змістовну кластеризацію "за побудовою". Всі вони можуть давати різні результати. По-друге, число кластерів, як правило, невідоме заздалегідь і встановлюється відповідно до деякого суб'єктивного критерію. По-третє, результат кластеризації істотно залежить від метрики, вибір якої, як правило, також суб'єктивний і визначається експертом [10].

Точні методи кластерного аналізу. Найбільш прямий спосіб розв’язання задачі кластеризації полягає в повному переборі всіх можливих розбиттів на кластери та знаходженні такого розбиття, яке веде до оптимального (мінімального) значення цільової функції. Методи повного перебору – єдина група методів, які дають змогу завжди відшукати оптимальний розв’язок. Проте така процедура практично нездійсненна за винятком тих випадків, коли n (число об’єктів) та m (число кластерів) невелике. Очевидно, що основним недоліком алгоритмів повного перебору є настільки великий обсяг обчислень, що, не зважаючи на високу швидкодію сучасних обчислювальних машин, в задачах із великою кількістю даних або суттєвою розмірністю вони непридатні. Тому використовують алгоритми граничного перебору, в яких кількість варіантів розбиття, що перебираються, скорочується. Найефективнішим із них є метод на основі динамічного програмування, який завжди забезпечує точний результат при значному зменшенні обчислювальної складності. Але навіть за такого підходу обсяг необхідних обчислень все одно залишається надзвичайно великим. За таких умов єдиним прийнятним методом на сьогодні є застосування наближених алгоритмів кластерного аналізу.

Методи ієрархічної кластеризації. За способом розбиття на кластери наближені алгоритми бувають двох типів: ієрархічні та неієрархічні.

Класичні ієрархічні алгоритми працюють тільки з категорійними атрибутами, коли будується повне дерево вкладених кластерів. Тут поширені агломеративні методи побудови ієрархій кластерів - в них проводиться послідовне об'єднання вихідних об'єктів і відповідне зменшення числа кластерів. Ієрархічні алгоритми мають ряд суттєвих обмежень: вони працюють лише з числовими даними, чутливі до викидів та вимагають задання порогових значень. Якщо не використовуються спеціально розроблені алгоритми скорочення розмірності, то застосування ієрархічних методів може вимагати обчислення та зберігання матриці подібності великої розмірності. Іншим недоліком є те, що об’єкти розподіляються по кластерах лише за один прохід, а погане початкове розбиття множини даних уже не може бути змінене на наступних кроках кластеризації. Третій недолік всієї родини ієрархічних алгоритмів полягає в тому, що вони можуть породжувати різні розв’язки в результаті простого перемішування об’єктів у матриці подібності. Результати також змінюються, якщо деякі об'єкти виключаються з розгляду. Необхідно відмітити, що стійкість є важливою властивістю кластеризації, якій ієрархічні алгоритми не задовольняють.

Хоча й існують досить ефективні ієрархічні алгоритми (AGNES, CURE, DIANA, BIRCH [14]), наведені недоліки роблять практично неможливим подальше підвищення їхньої швидкодії та точності отримуваних результатів. Із цих причин в даній роботі ієрархічні алгоритми кластерного аналізу не розглядаються.

Методи неієрархічної (оптимізаційної) кластеризації. Неієрархічні алгоритми базуються на оптимізації деякої цільової функції, що визначає оптимальне в певному сенсі розбиття множини об'єктів на кластери. У цій групі популярні алгоритми родини k-середніх (k-means), які в ролі цільової функції використовують суму квадратів зважених відхилень координат об'єктів від центрів шуканих кластерів. Кластери шукаються сферичної або еліпсоїдної форми. У канонічній реалізації мінімізація функції здійснюється на основі методу множників Лагранжа і дозволяє знайти тільки найближчий локальний мінімум. Серед неієрархічних алгоритмів, не заснованих на відстані, слід виділити EM-алгоритм (ExpectationMaximization). У ньому замість центрів кластерів передбачається наявність функції щільності ймовірності для кожного кластера з відповідним значенням математичного сподівання і дисперсією.

Всі описані вище методи розбивають вихідну множину об'єктів Х на декілька підмножин, що не перетинаються. При цьому будь-який об'єкт із Х належить лише одному кластеру.  Таке формулювання задачі кластеризації не позбавлене обмежень, серед яких обмеження на геометрію кластерів та повна відсутність врахування невизначеностей та викидів, присутніх у вхідних даних.

 

Методи нечіткої кластеризації

Відмінністю методів нечіткої кластеризації від чіткої є область визначення ступенів належності. Якщо за чіткої кластеризації ступені належності можуть приймати лише значення 0 або 1, таким чином відносячи об’єкт до одного з класів, то у випадку нечіткої кластеризації ступені належності можуть набувати будь-яких значень із інтервалу [0, 1]. Таким чином, нечітка кластеризація дозволяє віднести об’єкт до кількох, а в загальному випадку до всіх кластерів, але з різними ступенями належності. Зокрема ця особливість дозволяє більш достовірно описувати об’єкти, що знаходяться на межі кластерів, або об’єкти, рівновіддалені від центрів двох або більше кластерів.  Крім того, вона дає змогу врахувати невизначеності, що існують у даних, що також є суттєвою перевагою даного класу методів.

Інтерпретація результатів нечіткої кластеризації може бути дуже спірною, але в той же час створює найповніше уявлення про зв'язки між об'єктами. До того ж, в деяких випадках не можна виділити підмножини, що не перетинаються.

В цілому, основна перевага нечітких моделей в порівнянні з традиційними математичними моделями пов'язана з можливістю використання для їх розробки значно менших обсягів інформації про систему, причому вона може носити наближений характер.

Найпотужнішим засобом для розв’язання задачі в такій постановці є алгоритм FCM (Fuzzy c-means), що являє собою модифікацію EM-алгоритму.

В його основі лежить процедура нечіткої самоорганізації, а критерієм оптимальності є середньозважене відхилення точок-об’єктів від центрів кластерів:

 

 

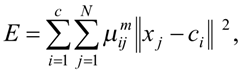
де - ступінь належності об’єкта j до кластера i,       

x_j – вектор ознак об’єкта j,

c_і – центр кластера і,

m ≥ 1 - експоненційна вага, що визначає нечіткість, розсіяність кластерів.

Початкові значення центрів кластерів c_j вибираються випадковим чином із областей допустимих значень відповідних компонент векторів x_j .

Основна ідея полягає в тому, що на кожній ітерації переобчислюється центр мас для кожного кластера, отриманого на попередньому кроці, після чого точки розбиваються на кластери знову відповідно до того, який із нових центрів виявився ближче за обраною метрикою. Алгоритм завершується, коли на деякій ітерації не відбувається зміни кластерів.

Перерахування координат центрів мас кластерів та ступенів належності відбувається за формулами:

 

        

 

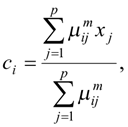
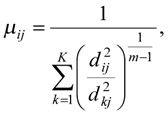
де  - Евклідова відстань між центром c_і та вектором x_j, .

Багаторазове повторення ітераційної процедури веде до досягнення мінімуму функції Е, який необов’язково буде глобальним мінімумом. Проте якість знайдених центрів суттєво залежить від попереднього вибору як значень , так і центрів c_j. Крім того, FCM використовує обмеження, подібне до того, що накладає на шуканий розв’язок теорія ймовірностей: сума ступенів належності і-тої точки до всіх кластерів  становить 1: 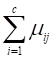  для всіх j. Таке обмеження має на меті уникнути тривіального розв’язку, коли всі ступені належності виявляються рівними 0, і дає змістовні результати в тих прикладних застосуваннях, де припущення про «ймовірнісну» природу ступенів належності має практичний сенс.

Але, оскільки ступені належності, отримані при такому обмеженні, відносні, вони непридатні в тих задачах, у яких ступінь належності точки до кластера повинен відображати її типовість, характерність саме для цього кластеру. Це повністю узгоджується з теорією нечітких множин Заде, адже ступінь належності точки до класичної нечіткої множини є абсолютною величиною, незалежною від ступенів належності цієї ж точки до інших нечітких множин, визначених на тій самій універсальній множині. Таке формулювання є більш придатним для більшості задач кластеризації, оскільки ступінь належності точки до кластера є мірою того, наскільки ця точка є носієм спільних характеристик кластеру, її типовості, і не повинен залежати від того, як вона розташована відносно інших кластерів. Можливісний підхід до визначення природи ступенів належності РСМ оперує ступенями належності, що володіють цією властивістю. Його авторами було переглянуто цільову функцію методу FCM таким чином, щоб при досягненні її мінімуму ступені належності для репрезентативних точок кластерів були високими, а для нерепрезентативних – низькими, незалежно від взаємного положення точок та кластерів. Результуючий функціонал має вигляд

 

(1.2)

 

де η_і – додатне число.

Значення η_і визначає відстань, на якій значення ступеня належності точки до кластера стає рівним 0,5.

За такої цільової функції відповідним чином змінюються також і формули для перерахунку змінних величин методу:

 

 

Співвідношення, що використовується для перерахунку координат центрів кластерів, порівняно з FCM залишається без змін:

 

 

Розв’язки, отримані при такому підході, більше відповідають дійсності та інтуїтивному уявленню про природу кластерів.