2.2 Нечіткі логічні системи типу 2

Одним із найбільш розповсюджених застосувань математичного апарату інтервальних нечітких множин при побудові нечітких логічних систем є розширення можливостей методів класу АНР. Більшість досліджень у цьому напрямку зосереджується на пошуку нових та вдосоналенні існуючих шкал порівняння альтернатив та побудові більш збалансованих шкал. При цьому залишаються в силі такі недоліки методу АНР як неврахування невизначеностей, пов’язаних із поданням суб’єктивного судження у кількісному вигляді та неможливість побудувати семантично адекватну ієрархію ознак в деяких задачах. У ряді робіт фігурують дев’ятиточкові шкали, що являють собою варіації оригінальної шкали Сааті, наведеної в таблиці 1.1. Всі вони мають трапецієвидні верхні та нижні функції належності; їхню висоту, як правило, приймають на рівні 1 та 0.8 відповідно, як наприклад для шкали в табл. 1.2.

Таблиця 1.2

Інтервальна шкала суджень

Подібні лінгвістичні змінні також використовуються  для визначення оцінок ваг альтернатив; з них найбільшою популярністю користується лінгвістична змінна, наведена в таблиці 1.3. Її так чи інакше використовує переважна більшість розробників методів на основі АНР.

Таблиця 1.3

Інтервальна лінгвістична змінна для оцінювання ваг альтернатив

Ряд сучасних досліджень присвячено адаптації методів класу TOPSIS – Technique for Order Preference by Similarity to Ideal Solution – групи методів багатокритеріальної оптимізації, які також ґрунтуються на порівнянні альтернатив – для інтервальних нечітких розрахунків. За допомогою цього підходу розв’язують задачі вибору оптимальної структури веб-додатків, оцінювання ризиків забруднення довкілля та вибору кращої серед альтернатив утилізації небезпечних відходів, вибору постачальника, вибору оптимального розташування виробничих потужностей підприємства . Авторами цих підходів також відзначається зручність використання інтервальних нечітких множин для подання значень оцінок та ваг критеріїв в умовах невизначеності, проте вони зазначають, що для побудови лінгвістичних змінних як правило залучаються експерти, які мають досвід у предметній галузі та володіють знаннями, необхідними для кваліфікованого оцінювання критеріїв та альтернатив. Такого роду обмеження є спільними для всіх моделей, побудованих виключно на основі експертних знань. Наряду з вичерпними знаннями з предметної галузі експерт повинен володіти базовими концепціями математичного моделювання, що значно звужує коло доступних експертів. Не зважаючи на цей недолік, автори досліджень стверджують, що саме застосування інтервальних нечітких множин дозволяє отримувати результати, що більш адекватно відображають реальність.

Інтервальні форми методу PROMETHEE (Preference Ranking Organization METHod for Enrichment Evaluations) дозволяють оцінити та вибрати альтернативу з деякого набору, вважаючи за основу критерії, що відображають переваги та недоліки альтернатив, та виконати ранжування альтернатив. Метод QUALIFLEX (QUALItative FLEXible) вважається перспективним для використання в контексті теорії інтервальних нечітких множин завдяки його можливостям обробки кількісної та якісної інформації одночасно. В основі методу лежить процедура парних порівнянь альтернатив відповідно до кожного критерію для всіх можливих перестановок альтернатив. Після цього обчислюються індекси відповідності та невідповідності для кожної пари альтернатив перестановок і визначається оптимальна перестановка альтернатив, яка максимізує значення індексу відповідності/невідповідності, та найкраща альтернатива.

Суть методу DEMATEL (Decision-Making Trial and Evaluation Laboratory) полягає в розрахунку непрямих відношень між змінними на основі оцінки прямих зв'язків для структуризації складних проблем. Виходячи з оцінки природи відношень між змінними, метод DEMATEL дозволяє поділити змінні на причини та наслідки. Змінна «причина» має значно більший вплив на інші змінні в порівнянні з впливом на неї саму.

Метод COPRAS (Complex Proportional Assessment) використовується для багатовимірного аналізу даних на основі значень максимізуючого та мінімізуючого критеріїв. При цьому обидва критерії розглядаються незалежно один від одного. Основна ідея методу – оцінка j-тої альтернативи Z ^j прямо пропорційна впливу, що його чинить максимізуючий критерій S^+j, та оберенено пропорційна сумі зважених нормалізованих значень мінімізуючого критерію S^-j . Серед його переваг відзначається обчислювальна простота, що є важливим фактором у роботі з нечіткими множинами другого та вищих порядків.

За останнє десятиліття подібну адаптацію математичного апарату нечітких множин було виконано також для інших підходів, в результаті чого з’явились методи IT2FDEA для Data Envelopment Analysis (DEA), IT2FELECTRE на базі методу ELECTRE (Interval Type-2 Fuzzy ELimination Et Choix Traduisant la REalité), IT2FENTROPY, IT2FLINMAP на основі методу LINMAP, Linear Programming Technique for Multidimensional Analysis of Preference, IT2FVIKOR як розширення методу VIKOR (VIseKriterijumska Optimizacija I Kompromisno Resenje, метод багатокритеріальної оптимізації та компромісного розв’язку) та ін.

В усіх розглянутих підходах до формування нечітких множин термів лінгвістичних змінних так чи інакше залучається експерт, що зумовлює використання простих форм функцій належності – трикутних або трапецієвидних. Вимога подання цих функцій відразу в інтервальній формі ще більше ускладнює роботу експерта, який, в загальному випадку, не обов’язково має необхідне для цього математичне підгрунтя. В той самий час, у порівнянні з многокутними гладкі функції належності, зокрема гаусова, мають ряд переваг, таких як ненульове значення в будь-якій точці області визначення та більш інтуїтивний характер (нормальний розподіл – найбільш поширений в природі). Крім того, гладкі функції належності неперервно диференційовні. У деяких роботах висловлюється думка про те, що відсутність неперервно диференційовної функції належності ускладнює процес навчання нечітких моделей. Гаусова ж функція, будучи неперервно та нескінченно диференційовною, дає можливість проведення теоретичного аналізу нечітких систем.

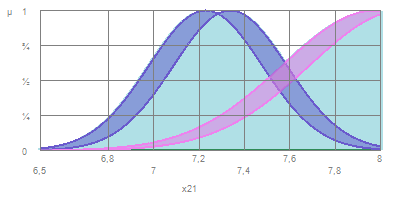
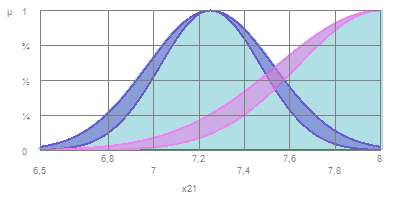
У випадку гаусових функцій можливі два типи первинних функцій належності інтервальних нечітких множин типу 2:

–   функції з невизначеним центром та сталим відхиленням (рис. 2.1, а);

–   функції зі сталим центром та невизначеним відхиленням (рис. 2.1, б).

                        а)                                                            б)

Рисунок 2.1 – Первинні функції належності

В межах першого підходу до синтезу нечітких моделей та побудови нечітких баз знань, коли архітектура нечіткої моделі встановлюється дослідником, інтервальна форма функції належності отримується емпіричним та як правило дещо штучним шляхом, наприклад приймаючи значення верхньої та нижньої функції належності на рівні 1 та 0.8 відповідно.

Існує також механізм побудови інтервальних нечітких функцій належності типу 2 з функцій належності типу 1 в межах третього підходу, що передбачає використання експериментальних даних для побудови функцій належності. Відповідно до нього, виконується зміна відповідного параметра незначними інкрементами доти, поки вихід нечіткої логічної системи типу 1 знаходиться в межах одного терму:

де  – початкові параметри функцій належності,

 – вихід системи без дефазифікації – номер терма з максимальним покриттям результуючою функцією належності. Форма інтервальної функції, отриманої таким чином, має прямий зв’язок із апроксимаційними властивостями моделі. Окрім власне зони невизначеності, яка застерігає від прийняття хибного точкового рішення, вона також являє собою змістовну характеристику ступеня невизначеності, асоційованої з об’єктом дослідження.