1. Методы и алгоритмы формирования контурных изображений

1.4. Интерполяция и аппроксимация кривых произвольного типа

1.4.2. Интерполяционные методы Лагранжа и Ньютона

К наиболее простым интерполяционным полиномам относят полином Лагранжа.

Пусть даны n+1 точек (x₀,y₀), (x₁,y₁), …, (x_n,y_n) на координатной плоскости, причем x_i<x_i+1, i=0,n. Интерполяционный полином Лагранжа n-ой степени для данного множества точек имеет вид

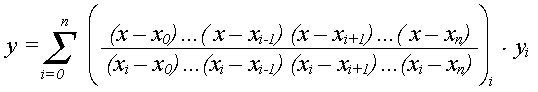
Возьмем для примера n=1. Тогда после подстановки в формулу находим

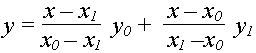
Полученное уравнение есть уравнением отрезка прямой линии, которое соединяет точки (x₀,y₀) и (x₁,y₁).

Полином Лагранжа – это не единственный многочлен, который отвечает задаче интерполирования. В действительности существует бесконечно много подходящих многочленов, но многочлен Лагранжа – это единственный многочлен степени n, являющийся решением задачи. Вместе с тем интерполяционный метод Лагранжа имеет ряд существенных недостатков:

*  поскольку степень многочлена Лагранжа определяется количеством узлов (минус 1), то любая попытка повысить точность аппроксимации путем увеличения количества узлов влечет за собой увеличению степени полинома;

*  формула для расчета достаточно громоздка. Каждое слагаемое формулы является многочленом n-ой степени;

*  если степень полинома выше 5, то на кривой появляется “волнистость”, которая получила название эффекта Рунге – Мерей. Возможно улучшить ситуацию путем подбора расположения узлов в зависимости от конкретной функции в интерактивном режиме, но такая процедура достаточно неудобна.  

Один из путей уменьшения волнистости состоит в разбиении интервала интерполирования на несколько подинтервалов, для каждого из которых формируют многочлены Лагранжа, но уже более низких степеней. В дальнейшем многочлены Лагранжа «склеивают», однако объединенная аппроксимирующая функция может быть недифференцируемой на границах подинтервалов.  

При равномерной дискретизации (Dх=const) удобно пользоваться интерполяционной формулой Ньютона. Чтобы записать формулу Ньютона введем понятие о так называемых разностях функции.  

Пусть заданы значения аргумента a, a+h, a+2h, a+3h, … и соответствующие значения функции. Выпишем значения аргумента и функции двумя колонками. Затем каждое число второй колонки, начиная с первого, вычтем из последующего числа. Получим первые разности функции и первую из них обозначим через Df(a). Найденные разности записываем в третьей колонке. Аналогично по первым разностям составляем вторые. Первую из вторых разностей обозначим символом D²f(a). Подобно составляются третьи разности и т.д. Интерполяционная формула Ньютона имеет вид   

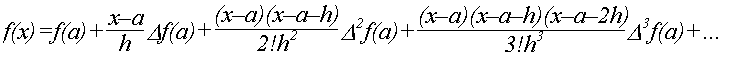
Заметим, что полином Ньютона третьего порядка по сравнению с полиномом Ньютона второго порядка позволяет повысить точность восстановления лишь в 1,5 раза.  

При добавлении новых узлов приведенная формула более удобна для вычисления, чем запись интерполяционного многочлена в форме Лагранжа, т.к. добавление новых узлов интерполяции влечет вычисление только новых слагаемых, добавляемых к тем, которые были вычислены с меньшим числом узлов. При использовании формы Лагранжа в этой ситуации требуется выполнять все вычисления заново. 

Контрольные  вопросы.

1.  Какой из интерполяционный полиномов имеет наименьшую степень?

2.  В чем состоят недостатки метода Лагранжа?

3.  В каких случаях удобно использовать метод Ньютона?

4.  Как избежать эффекта Рунге-Мерей?

     Содержание