1. Методи та алгоритми формування контурних зображень

1.3. Методи та алгоритми формування кривих другого порядку

 1.3.3. Гіпербола

Гіперболічний інтерполятор реалізує функцію виду А=XY. Оцінювальна функція для нього має слідуючий вид

U_ij = X_iY_i – A

При U≥0 виконується крок по осі Y (рис.1.14), а при U<0 – крок по осі X, причому X_i+1=X_i+1, а Y_i+1=Y_i–1. Після кроку по осі X нове значення оцінювальної функції обчислюється як U_i+1,j=U_ij+Y_j, а після кроку по осі Y: U_i,j+1=U_ij–X_i. 

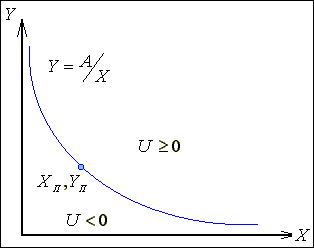
Рис. 1.14. Формування оцінної функції при игіперболічній гіперболяції

Якщо обхід гіперболи буде протилежним до розглянутого випадку, тобто X_i+1=X_i+1, а Y_i+1=Y_i–1, то зміниться на протилежне корегування оцінювальної функції.

При реалізації алгоритмів з восьмивекторною орієнтацією крокових приростів, при діагональному переміщенні нове значення оцінювальної функції має вигляд:

U_i+1,j+1 = U_ij + Y_j – X_i

Контрольні   запитання.

1.  Назвіть області застосування гіперболічної інтерполяції.  

2.  Знайдіть значення оцінювальної функції для різних обходів гіперболи.

     Зміст