1. Методи та алгоритми формування контурних зображень

1.3. Методи та алгоритми формування кривих другого порядку

 1.3.4. Еліпс

Рівняння еліпса в полярній системі координат має вигляд :   

X = a cos,

Y = b sin,

де a, b – розміри еліпса по осях Х і Y відповідно.

Стосовно процедури формування еліпса справедливі усі положення, розглянуті при побудові кола, з врахуванням наступних особливостей:

*  опорним фрагментом є точка одного з квадрантів ;

*  для для еліпса довжина радіус- вектора R_i= √(X²_i+Y²_i) крок приросту полярного кута DQ_i=1/R_i є змінними та повинні обчислюватися на кожному кроці.

Розглянемо формування еліпса за методом оцінювальної функції:   

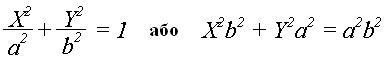
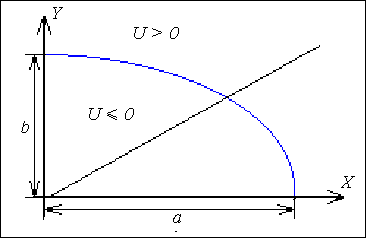
Рис. 1.15. Формування оцінної функції при еліптичній інтерполяції

Оцінювальна функція  

U_ij = X²b² + Y²a² = a²b²

за еліпсом (рис. 1.15) має додатне значення, всередині його - від’ємне. Для першого квадранта при U_ij≥0 виконується крок по осі Y і Y_i+1=Y_i–1, а при U_ij<0 – крок по осі Х. При цьому X_i+1=X_i+1.

Після кроку по осі Y 

U_i,j+1 = b²X_i²+a²(Y_j–1)²–a²b² = b²X_i²+a²Y_j²+2a²Y_j+a²–a²b² = U_ij+2a²Y_j+a²  

Аналогічно можна показати, що після виконання кроку по осі X X нове значення оцінювальної функції буде мати вид  

U_i+1,j = U_ij + 2b²X_i + b²

Приведені формули показують, що після кожного кроку необхідно виконувати операцію множення , що суттєво обмежує швидкодію формування крокової траєкторії . 

Контрольні   запитання.

1.  Назвіть характерні особливості еліптичного інтерполювання.

2.  Які методи застосовують для еліптичного інтерполювання ?

3.  Дайте порівняльну характеристику колового та еліптичного інтерполювання за методом оцінювальної функції.

     Зміст