1. Методи та алгоритми формування контурних зображень

1.4. Інтерполяція та апроксимація кривих довільного типу

1.4.2. Інтерполяційні методи Лагранжа та Ньютона

До найбільш простих інтерполяційних поліномів відносять поліном Лагранжа.

Нехай задано n+1 точок (x₀,y₀), (x₁,y₁), …, (x_n,y_n) на координатній площині, причому x_i<x_i+1, i=0,n. Інтерполяційний поліном Лагранжа n-го степеня для даної множини точок має вигляд

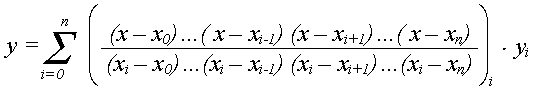
Візьмемо для прикладу n=1. Тоді після підстановки в формулу маємо

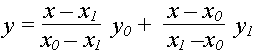
У результаті отримано рівняння відрізка прямої лінії, яка з`єднує точки (x₀,y₀) и (x₁,y₁).

Поліном Лагранжа – це не єдиний багаточлен, який відповідає задачі інтерполювання. У дійсності існує нескінченно багато відповідних багаточленів, але багаточлен Лагранжа єдиний багаточлен степені n, який є розв`язком задачі. Разом з цим інтерполяційний метод Лагранжа має ряд істотних недоліків:

*  оскільки степінь багаточлена Лагранжа відповідає кількості вузлів (мінус 1) і будь-яка спроба покращити точність апроксимації шляхом збільшення кількості вузлів викликає збільшення степеня полінома;

*  формула для розрахунку лосить громістка. Кожен додаток фориули є багаточленом n-го степеня;

*  Якщо степінь полінома більший 5, то кривій з’являється “хвилястість”, яка одержала назву ефекту Рунге - Мерей. Можливо поліпшити ситуацію щляхом підбора розташування вузлів у залежності від конкретної функції в інтерактивному режимі, але така процедура досить незручна.

Один із шляхів зменшення хвилястості полягає в розбитті інтервалу інтерполяції на декілька підінтервалів, для кожного з яких формують многочлени Лагранжа, але уже більш низького степення. В пожальшому многочлени Лагранжа "склеюють", однак об'єднана апроксимаційна функція може бути недиференційна на границях підінтервалів.  

При рівномірній дискретизації (Dх=const) зручно користуватися інтерполяційною формулою Ньютона. Щоб записати формулу Ньютона введемо поняття про різниці функції.  

Нехай задані значення аргументу a, a+h, a+2h, a+3h, … і відповідні значення функції. Випишемо значення аргументу і функції двома колонками. Потім кожне число другої колонки, починаючи з першої, віднімемо з наступного числа. Одержимо перші різниці функції і першу з них позначимо через Df(a). Знайдені різниці записуємо в третю колонку. Аналогічно по перших різницях складаємо другі. Першу з других різниць позначимо символом D²f(a). Подібно складаються треті різниці і т.д. Інтерполяційна формула Ньютона має наступний вид    

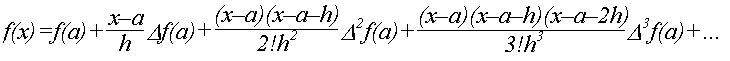
Зауважимо, що поліном Ньютона третього порядку в порівнянні з поліном Ньютона другого порядку дозволяє підвищити точність відновлення лише в 1,5 раз.  

&При введені нових вузлів приведена формула більш зручна для обчислення, чим запис інтерполяційного багаточлена у формі Лагранжа, тому що додавання нових вузлів інтерполяції спричиняє обчислення тільки нових доданків, що добавляються до тих, які були обчислені з меншим числом вузлів. При використанні форми Лагранжа в цій ситуації потрібно виконувати всі обчислення знову

Контрольні   запитання.

1.  Який із інтерполяційних поліномів має найменший степінь?

2.  В чому полягають недоліки метода Лагранжа ?

3.  В яких випадках зручно використовувати метод Ньютона ?

4.  Як уникнути ефекту Рунге-Мерей ?

     Зміст