1. Методи та алгоритми формування контурних зображень

1.4. Інтерполяція та апроксимація кривих довільного типу

1.4.3. Апроксимація кривих методом Безьє

На практиці є ряд задач, в яких необхідно не точне наближення, а згладжене формування фігури, що апроксимує вхідні дані, тобто коли властивості апроксимації в цілому важливіші точності наближення і коли вимоги, які пред’являються об’єкту, що проектується, не можуть бути достатньо просто виражені математично.

Досить типова задача має місце в процесі проектування автомобілів. Вона заключається в знаходженні математичного представлення для малюнка чи глиняної моделі, що її запропонував дизайнер. В цьому випадку неможливо визначити “найкраще” наближення. Якість наближення залежить головним чином від думки дизайнера. Отже, логічно використовувати інтерактивний метод, що дозволяє користувачу експериментувати з різноманіттям форм, причому від нього не потребується ніяких знань про використані математичні методи. Проектування таким способом значно полегшується, якщо є можливість керувати формою кривої за допомогою зміни невеликої кількості параметрів, особливо, якщо ці параметри задавати в графічному вигляді.

Розроблено цілий ряд методів для авіаційної, автомобільної та суднобудівельної промисловості, найбільш поширеним серед яких є метод Безьє, що використовує аппроксимацію багаточленами Бернштейна.

Замість безпосереднього використовування точок, для завдання багаточлена, використовують множину точок-орієнтирів. Якщо (X₀,Y₀), (X₁,Y₁), ..., (X_m,Y_m) – вказані точки- орієнтири, то відповідний багаточлен Безьє визначається як

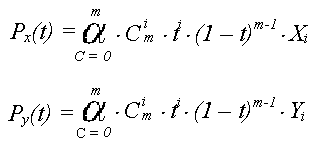
де                

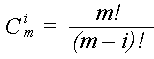
Остання формула достатньо складна, тому на практиці використовують вираз вигляду:  

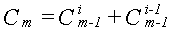
Багаточлени Безьє мають такі властивості:

P(0)=P₀ , P(1)=P_m, при t=0,1.

Вказане визначає те, що крива Безьє проходить через першу та останню точки -орієнтирів. Всі інші вершини ламаної в загальному випадку не лежать на кривій Безьє.

Якщо використовувати диференційне числення, то можна показати, що крива Безьє розміщена всередині опуклої оболонки множини точок-орієнтирів. Нахил дотичних векторів в крайніх точках кривої співпадає з нахилом відповідно першої та останньої ланок ламаної Безьє.

Багаточлени Безьє задовольняють теоремі Веєрштрасса, тобто вони рівномірно зходяться до апроксимуючої функції з ростом m.

Не дивлячись на ці позитивні якості, багаточлени Безьє ніколи не використовувались широко для побудови апроксимацій з мінімальною нормою відхилення. Причина у тому, що багаточлени Безьє дуже повільно зходяться у рівномірній нормі. Однак для багаточленів Безьє достатньо просто, порівняно з іншими методами, написати програми.

В процесі інтерактивного конструювання не ставиться задача точності, а потребується засіб керування формою.

Практичне конструювання за методом Безьє таке.

Спочатку конструктор вручну робить малюнок бажаної кривої. Потім він вказує на вершини ламаної кривої, яка є, по суті, першим наближенням. Наступний крок складається в переміщенні вершин таким чином, щоб поступово покращити наближення. Якщо необхідно, деякі вершини видаляються чи додаються нові. 

Контрольні   запитання.

1.  Чим визначається степінь полінома Безьє ?  

2.  Назвіть характерні особливості апроксимації Безьє .  

3.  Як практично здійснюється апроксимація кривих за методом Безьє ?

4.  Порівняйте обчислювальну складність інтерполювання за методом Лагранжа та апроксимацію за методом Безьє

     Зміст