1. Методи та алгоритми формування контурних зображень
1.4. Інтерполяція та апроксимація кривих довільного
типу
1.4.4. Сплайнова інтерполяція
Методи апроксимації функцій за допомогою сплайнів, запропоновані вперше в 40-х роках, одержали широке поширення лише останнім часом.
Основний недолік інтерполяційних багаточленів як апарата наближення функцій, застосовуваного для відновлення дискретизованих сигналів, полягає в тому, що поводження цих багаточленів в окрузі якоїсь точки визначає їхнє поводження в цілому. Якщо досліджуваний сигнал на різних ділянках має різний характер , наприклад на одній ділянці постійний, а потім круто зменшується або зростає і т.д. , то використання інтерполяційних багаточленів прийнятних результатів не дає. У таких випадках краще користуватися сплайнами.
Англійське слово spline
означає «гнучка рейка». Таку рейку використовують у якості гнучкого лекала при кресленні плоских кривих по опорних точках.
Основна ідея застосування сплайнів полягає в наступному.
Інтервал, на якому відновлюють функцію розбивають на підінтервали (рис.1.16), на кожному з який функцію задають поліномом достатньо
низького степені і забезпечують неперервність кривої в точках “склейки” шляхом прирівняння значень поліномів на межах підінтервалів.
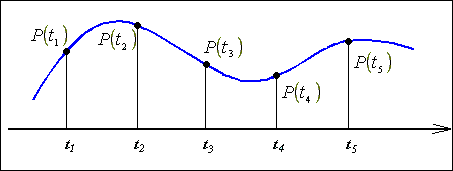
Рис. 1.16.
Відновлення сигналу за допомогою сплайнів.
При цьому важливою умовою є також неперервність декількох похідних.
Таким чином, сплайном Pn
називають сукупність багаточленів
Pni
ступеня
n,
заданих на i-тому
кроці дискретизації ,які задовольняють умові
Pni(ti)
= Pn(i-1)(ti),
тобто ступеня n
сплайн- функціями, складеними з «шматочків» багаточленів даного ступеня, що сполучені так, щоб функція, що утворилася, була безперервною і мала декілька неперервних похідних.
Таким чином, сплайн є кусочно-поліноміальною функцією. Сплайн нульового степеня збігається зі східчасто-інтерпольованою функцією, а сплайн першого степеня - із лінійно-інтерпольованою. Слід зазначити, що сплайни другого і більш високого степеня не будуть збігатися з інтерполяційними поліномами відповідних степенів.
Відомо, що коли однорідний брус закріпити в двох довільних точках і надати його осі заданий нахил у цих точках, то форма кривої бруса описується поліном третього степеня.
Припустимо, що кубічна парабола, задана в параметричній формі
P(t) = a3t3 + a2t2 + a1t + a0
проходить через дві точки P(t1)
и
P(t2),
у яких відомі значення похідних
Р/(t1)
и Р/(t2).
Це означає, що задані чотири необхідних і достатніх умови для визначення чотирьох невідомих коефіцієнтів у приведеному вище виразі. Цей багаточлен іноді називають кубічним інтерполяційним багаточленом Ерміта.
Параметричне представлення кривої має ту перевагу, що можна вибрати довільний діапазон зміни параметра. Для простоти обчислювального процесу будемо вважати, що параметр t
у межах кожного сегмента змінюється в діапазоні від 0
до
1
(0≤t≤1).
Неважко помітити, що
Визначимо похідну
Р/(t):
Р/(t)=3a3t2+2a2t+
a1.
Звідси випливає, що
З приведених виразів легко визначити невідомі
a0,
a1, a2, a3:
a0=P(0),
a1=Р/(0),
a2=3
Розглянута процедура виконується для кожної пари заданих точок кривої. Так, визначивши кубічну параболу між точками P(t1)
и
P(t2)
на інтервалі t1t2,
для знаходження наступної такої дуги кривої на інтервалі
t2t3
необхідно на межі інтервалу (точка
t2)
прирівняти значення як самих функцій , так і їх перших похідних, тобто виконати “склеювання”.
Знайдемо вираз для кубічної кривої X(t)
у формі Ерміта в матричній формі, якщо відомі кінцеві точки і дотичні вектора до кривої у цих точках.
Визначимо, що Р1,
Р4 – точки; R1,
R4 –
дотичні.
X(0)
= P1x
X(1) = P4x
X(0)
= R1x
X(1) = R4x
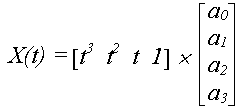
або
X(t) = TCx (*),
де T
=
[t3,
t2,
t,
1],
X(0) = P1x = [0,0,0,1]Cx,
X(1)
= P4x = [1,1,1,1]Cx ,
X/(t)
= [3t2, 2t, 1,
0]Cx,
X/(0) = R1x = [0,0,1,0]Cx,
X/(1) = R4x = [3,2,1,0]Cx.
P1 0, 0, 0, 1
P4 1, 1, 1, 1
R1 0, 0, 1, 0
R4
3, 2, 1, 0
Перевертаючи матрицю розміром 4x4,
отримуємо
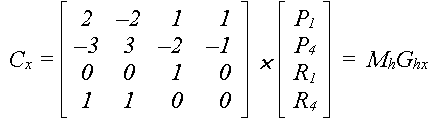
Mh
–
називається матрицею Ерміта, Ghх
–
геометричним вектором Ерміта.
Підставивши Сx
в (*),
отримаємо:
Знайдемо добуток
ТМ:
Перемножуючи цей вираз справа на Ghx,
отримаємо:
Чотири отриманих функції іноді називаються функціями спряженості.
За допомогою перших двох функцій визначаються точки Р1
і Р4,
а за допомогою решти отримаємо згладжене об’єднання. Причому, чим більший дотичний вектор, тим крутіша сама крива.
До недоліків такого підходу варто віднести необхідність завдання похідних у вузлах . Для їхнього обчислення використовують ряд підходів.
Найбільше просто використовувати замість похідних їхні наближені значення, отримані в результаті інших апроксимацій. Наприклад, для кожного вузла за значеннями функцій у найближчих2m
вузлах будується багаточлен степені2m+1,
похідні якого потім використовуються для побудови ермітового сплайна.
При завданні кривої у формі Безьє для знаходженян похідних
P/(ti)
и
P/(ti+1)
використовуються дві додаткових точки (рис. 1.17) Ri
і Ri+1,
які задають два датичні вектора P(ti)Ri
и
P(ti+1)Ri+1.
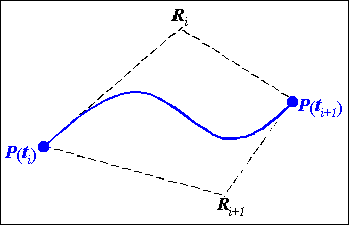
Рис. 1.17.
Знаходження похідних за методом Безьє
Похідні
P/(ti)
і P/(ti+1)
визначаються п онаступним виразам:
R1=3(P2–P1)=P’(0),
R4=3(P4–P3)=P’(1).
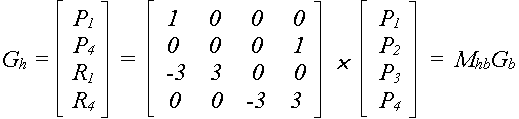
Це співвідношення між матрицею Ерміта Gh
та геометричною матрицею Бєзьє. Підставляючи отримані значення, знаходимо
Позначимо добуток
MhMb
через
М
отримаємо вираз
X(t)=TMGb,
котрий зараз має форму Бєзьє.
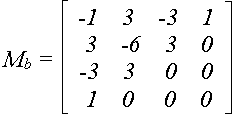
Форма Бєзьє використовується у машинній графіці частіше, ніж форма Ерміта . Причиною цьому є :
* по-перше, у випадку форми Ерміта дотичні вектори повинні задаватися у явному вигляді. У формі Бєзьє дотичні находять “локатором”;
* по-друге , у формі Бєзьє чотири точки задають випуклий багатокутник, що можна виконати гумовою ниткою.
Знайдемо
Х
= TMbGb.
Можна показати, що сума всіх коефіцієнтів біля
t
дорівнює
1,
що визначає оптимальне середнє значення для чотирьох керуючих точок.
Розроблено підхід, відповідно до якого похідні в проміжних точках знаходять шляхом рішення матричного рівняння виду:
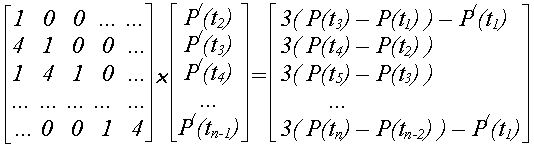
Підхід базується на рівності на межах інтервалів перший і других похідних. З приведеного матричного виразу знаходять похідні, подані другою матрицею в лівій частині рівняння. Таким чином, у даному підході в якості вихідних задаються всі базові точки, через які проходить крива, а також похідні в початковій і кінцевій точках.
Інші методи визначення відсутніх параметрів для побудови сплайнів базуються на накладенні деяких додаткових умов, що призводить до необхідності рішення системи рівнянь, що виражає ці умови.
У загальному випадку, коли в моменти часу
e=0,1,2,…
задано дискретні відліки сигналу x0,
x1,
x2,…,
&сплайн-функция, що відновлює дискретизованний сигнал
n-го ступеня має вид
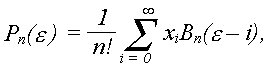
де
Bn(e)
–
деякий сплайн степеня n
(B-сплайн Шенберга), який називається ядром сплайна. Функція Bn(e)
задається наступним чином:
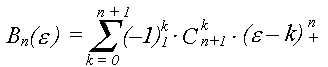
де
C![]() –
число сполучень із (n+1)
по k.
–
число сполучень із (n+1)
по k.
При переході від інтерполяції багаточленами до інтерполяції сплайнами переслідуються дві цілі. Перша, це покращання якості наближення: при однакових обчислювальних витратах абсолютні похибки інтерполяції сплайнами менші, чим похибки інтерполяції багаточленами, а при однакових похибках зменшується обсяг обчислень. Сплайни дозволяють уникнути осцилляций. Для рішення задачі збіжності накладаються більш слабкі вимоги, чим у випадку багаточленів. Наприклад, інтерполяція сплайнами невисоких степенів сходиться навіть для неперервних функцій.
Друга цель - різке зменшення обчислювальних витрат, оскільки при побудові алгоритмів рішення задач , так і при подальшій роботі з аппроксимантами використовуються багаточлени невисоких степенів або інші елементарні функції.
При роботі зі сплайнами можна використовувати або кусочно-багаточленне представлення, або представлення через базисні функції. У першому випадку досягається найбільша економія арифметичних операцій, але необхідно зберігати великий об’єм інформації про багаточлени. В другому випадку маємо зворотне.
Контрольні
запитання.
1.
В чому полягають переваги сплайнової інтерполяції по відношенню до інтерполяції по методу Лагранжа ?
2.
Яка мінімальна степінь полінома використовується в сплайновій інтерполяції ?
3. В чому відмінність обчислювального процесу при формуванні кривих Єрміта та Безьє ?
4. Якими шляхами знаходять похідні на границях інтервалів при сплайновій інтерполяції ?
5. 5. Які цілі переслідуються при переході від інтерполяції багаточленами до інтерполяції сплайнами ?