РОЗДІЛ 3 ЧАСОВІ РЯДИ, МЕТОДИ АНАЛІЗУ ЧАСОВИХ РЯДІВ
3.1 Основні поняття
Часовий ряд (time series) – це сукупність вимірювань деякої змінної величини, які проводяться у часі.
Характерною особливістю часових рядів є те, що спостереження за деяким об'єктом проводяться послідовно в часі.
Наприклад, температура повітря в середині кожної години доби, щорічна врожайність зернових, щоденний об'єм продажів якого-небудь товару, вартість акції підприємства, рівень інфляції, обмінний курс валют – все це часові ряди.
На pис. 3.1 зображено приклад часового ряду, що являє собою зміну рівня інфляції в США протягом певного часового періоду.
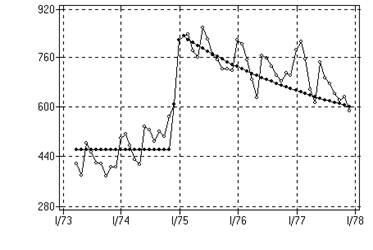
Рисунок 3.1 - Приклад часового ряду «Безробіття в США»
Для аналізу часового ряду порядок у послідовності є суттєвим, тобто час виступає одним із визначальних чинників. Це відрізняє часовий ряд від звичайної випадкової вибірки, де індекси вводять лише для зручності ідентифікації. Принциповою відмінністю часового ряду від простих статистичних сукупностей є:
- по-перше, рівні часового ряду не є незалежними. Інакше кажучи, якщо майбутні значення змінної можна визначити, то вони є функцією від минулих значень цієї змінної;
- по-друге, рівні часового ряду неоднаково розподілені. Закон розподілу ймовірностей цих випадкових величин і, зокрема, їхні математичні сподівання та дисперсії можуть залежати від часу.
Незалежно від природи кожного часового ряду можна виділити такі основні типи задач, які звичайно вирішують при проведенні аналізу початкових даних.
На першому етапі намагаються побудувати просту математичну систему або модель, яка описує поведінку часового ряду в короткій формі.
Потім робиться спроба пояснити його поведінку за допомогою інших змінних і з'ясувати ступінь зв'язку як між спостереженнями одного ряду, так і між різними рядами [7].
Виходячи з цілей дослідження, кожний часовий ряд звичайно розглядають як суміш таких компонент:
– тренд (trend) або довгострокова тенденція в розвитку ряду;
–сезонна компонента або, іншими словами, деякий ефект в динаміці ряду, який повторюється через певний період.
Розподіл динаміки часового ряду на вищезгадані компоненти визначає і групи математичних методів, які використовуються для аналізу відповідної компоненти.
Так для виявлення і аналізу тренда використовують апарат регресійного аналізу (regression analysis) і ковзних середніх. Для аналізу сезонного ефекту застосовують спеціальні моделі сезонного згладжування і сезонної авторегресії. Існує навіть спеціальний клас моделей, призначений для побудови і прогнозування (prediction) наслідків інтервенцій.
Коливання щодо тренда виявляються за допомогою спектрального аналізу, а для опису і прогнозування таких процесів використовують гармонійні моделі або моделі авторегресії – наприклад, метод ковзного середнього.
В теорії обробки часових рядів існує безліч способів їх згладжування: фільтрація з використанням перетворення Фур’є, кускова апроксимація многочленами та ін.
В задачах прогнозування часові ряди використовуються за наявності значної кількості реальних значень даного показника з минулого і за умови, що тенденція, яка намітилася у минулому, чітка і відносно стабільна. При цьому неявно передбачається, що минуле є хорошим провідником в майбутнє. Аналіз часових рядів дозволяє зумовити, що повинно відбутися за відсутності втручання ззовні, і, значить, не може передбачити зміни тенденції. Тим самим, подібним аналізом переважно користуються при складанні короткострокових прогнозів.
Криві тренда згладжують динамічний ряд значень показника, виділяючи загальну тенденцію. Саме вибір кривої тренда, що сам по собі є досить важкою задачею, багато в чому визначає результати прогнозування.
В більшості випадків динамічний ряд, окрім тренда і випадкових відхилень від нього, характеризується ще сезонними і циклічними складовими. Циклічні складові відрізняються від сезонних більшою тривалістю і непостійністю амплітуди. Звичайна тривалість сезонної компоненти вимірюється днями, тижнями або місяцями, а циклічної – роками або десятками років.
До основних методів аналізу часових рядів можна віднести метод ковзного середнього, експоненціального згладжування і проектування тренда. Для розгляду, як працюють ці методи, користуватимемося одним і тим же часовим рядом.
Приклад 1. Припустимо, що об'єми продажів деякого товару описуються в перебігу тижня часовим рядом:
День тижня |
Кількість проданої продукції |
Понеділок |
10 |
Вівторок |
6 |
Середа |
5 |
Четвер |
11 |
П'ятниця |
9 |
Субота |
8 |
Неділя |
7 |
Або дещо по-іншому
x |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
t |
10 |
6 |
5 |
11 |
9 |
8 |
7 |
3.2 Метод рухомого (ковзного) середнього
Цей метод розділяють на 2 типи: метод рухомого (ковзного) середнього і метод зваженого (ковзного) середнього.
Метод рухомого (ковзного) середнього.
Цей метод полягає в тому, що розрахунок показника на прогнозований момент часу будується шляхом усереднювання значень цього показника за декілька попередніх днів.
Припустимо, що у нас є дані показника тільки за перші три дні. Обчислимо прогнозоване число дефектів на четвертий день тижня (четвер). Для цього визначимо середнє значення числа дефектів за попередні три дні – понеділок, вівторок і середу – і знайдемо їх середнє арифметичне:
Прогнозований об'єм продажів на п'ятницю обчислюється аналогічним чином по реальних показниках за три попередні дні – вівторок, середу і четвер:
Подібним способом розраховуються прогнози на суботу, неділю і черговий понеділок:
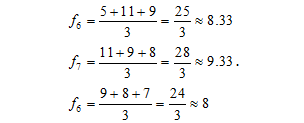
В результаті можна отримати таку таблицю
x |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
t |
10 |
6 |
5 |
11 |
9 |
8 |
7 |
- |
f |
- |
- |
- |
7 |
7.33 |
8.33 |
9.33 |
8 |
Порівняльні результати наведені на рис. 3.2: темними точками відзначені реальні значення, а світлими – прогнозовані.
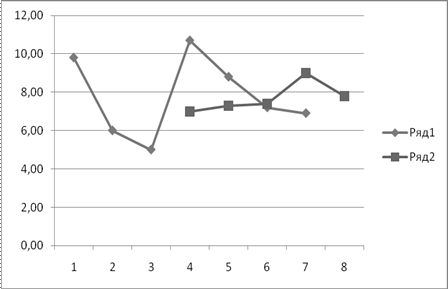
Рисунок 3.2 – Порівняльні результати прогнозу методом ковзного середнього
Для загального випадку розрахункова формула виглядає так:
або
де
– реальне значення показника у момент часу tk-i; N – число попередніх моментів часу; fk – прогноз на момент часу tk.
Метод зваженого (ковзного) середнього.
При прогнозуванні методом усереднювання часто доводиться спостерігати, що ступінь впливу використаних при розрахунку реальних показників виявляється неоднаковим, при цьому звичайно більш «свіжі» дані мають більшу вагу [7, 8]. Математично метод зваженого рухомого середнього можна записати як
де xk-i – реальне значення показника у момент часу;
N – кількість попередніх моментів часу, що використовуються при розрахунку;
fk – прогноз на момент часу tk;
wi – вага, з якою використовується показник xk-i при розрахунку.
Вага – це завжди додатне число. У разі, коли вся вага однакова, ми одержуємо формулу (3.1).
Для розрахунків звернемося до початкового часового ряду з прикладу 1, вважаючи, що при складанні прогнозу на завтрашній день об'єм сьогоднішніх продажів береться з вагою 60, вчорашніх – з вагою 30, а позавчорашніх – з вагою 10.
Маємо:
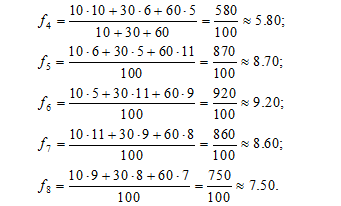
Результати розрахунків наведені в таблиці.
x |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
t |
10 |
6 |
5 |
11 |
9 |
8 |
7 |
- |
f |
- |
- |
- |
5,8 |
8,7 |
9,2 |
8,6 |
7,5 |
На рис. 3.3 темними точками відзначені реальні значення, а світлими – прогнозовані.
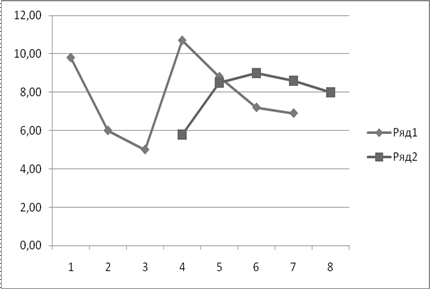
Рисунок 3.3 – Порівняльні результати прогнозу методом зваженого ковзного середнього
3.3 Метод експоненціального згладжування
Експоненціальне згладжування – це дуже популярний метод прогнозування багатьох часових рядів. Історично метод був незалежно відкритий Броуном і Холтом.
При розрахунку прогнозу методом експоненціального згладжування (exponential smoothing) враховується відхилення попереднього прогнозу від реального показника, а сам розрахунок проводиться за такою формулою
де α – стала згладжування (0 < α < 1).
Коли ця формула застосовується рекурсивно, то кожне нове згладжене значення (яке є також прогнозом) обчислюється як зважене середнє поточного спостереження і згладженого ряду. Рекомендується як f0 брати початкове значення, що дає якнайкращий прогноз.
Очевидно, результат згладжування залежить від параметра α. Якщо α дорівнює 1, то попередні спостереження повністю ігноруються. Якщо α дорівнює 0, то ігноруються поточні спостереження. Значення α між 0 і 1 дають проміжні результати.
З формули (4) виходить, що α має потрапляти в інтервал між 0 і 1 . На практиці звичайно рекомендується брати α менше 0,3. Крім того, параметр згладжування α часто знаходиться пошуком на сітці. Можливі значення параметра α розбиваються сіткою з певним кроком. Наприклад, розглядається сітка значень α від α = 0,1 до α = 0,9, з кроком 0,1. Потім вибирається той α, для якого сума квадратів (або середніх квадратів) залишків (значення, що спостерігаються, мінус прогнози на крок вперед) є мінімальною.
Для розрахунків знов звернемося до початкового часового ряду, вважаючи, що α = 0,2 і що прогноз на понеділок дорівнює 8.
Результати зведені в таблицю.
x |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
t |
10 |
6 |
5 |
11 |
9 |
8 |
7 |
- |
f |
- |
8,4 |
7,92 |
7,34 |
8,07 |
8,26 |
8,21 |
7,93 |
На рис. 3.4: темними точками відзначені реальні значення, а світлими – прогнозовані.
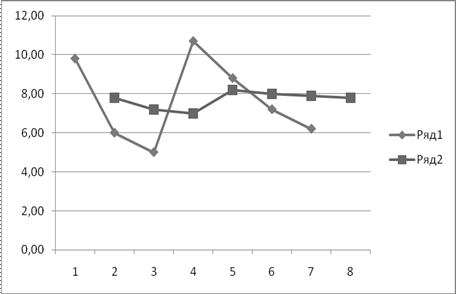
Рисунок 3.4 – Порівняльні результати прогнозу методом експоненціального згладжування
Слід мати на увазі, що при розв’язанні реальної задачі прогнозування часовий ряд складається у декілька етапів, і реальне значення показника на момент часу, що розраховується, як правило, наперед невідоме. Проте, перш ніж заглянути в майбутнє за допомогою одного з вказаних вище методів, звичайно проводяться розрахунки з повним часовим рядом, що описує деякий проміжок часу у минулому. Це робиться для того, щоб підібрати відповідне значення f0 і порівняти результати прогнозу з реальними даними (метод простого ковзного середнього), підібрати відповідні значення f0 та вагів і порівняти результати прогнозу з реальними даними (метод зваженого ковзного середнього) [7, 8].
3.4 Метод проектування тренда
Основною ідеєю методу проектування тренда є побудова прямої, яка «в середньому» якнайменше відхиляється від масиву точок (t, x) заданого часового ряду (див. рис. 3.5), що описується рівнянням:
де а, b – сталі коефіцієнти.
Розрахунок коефіцієнтів а і b ведеться за методом найменших квадратів.
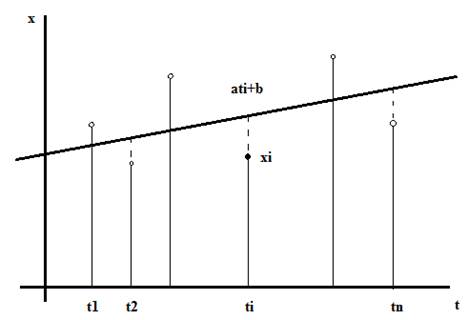
Рисунок 3.5 – Тестовий часовий ряд
Щоб знайти коефіцієнти а і b, виконують такі дії: для кожного значення t і змінної х, користуючись формулою (3.5), обчислюють відповідне значення змінної 
Потім знаходять різницю 
яку потім підносять до квадрату (щоб не думати про знак): 
Функція приймає мінімальне значення у тому випадку, коли величини а і b задовольняють таку лінійну систему:
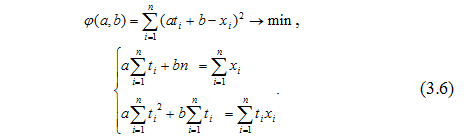
Ця система завжди має єдине рішення.
Розглянемо конкретний приклад, знов використавши часовий ряд з прикладу 1. Складемо допоміжну таблицю:
ti |
xi |
ti xi |
|
1 |
10 |
10 |
1 |
|
|
|
|
В такому випадку система рівнянь для обчислення коефіцієнтів а і b набуде такого вигляду:
Розв’язавши систему, отримуємо:
Тоді 
– рівняння шуканого тренду.Розрахунок показника для наступного дня за допомогою отриманого рівняння тренду проводиться наступним чином: 
На рис. 3.6 показано реальну та прогнозовану криві, побудовані за допомогою методу проектування тренда.
Точність прогнозу далі можна оцінити за допомогою кореляційного аналізу [8].
Наведені вище методи не вичерпують різноманіття методів аналізу часових рядів, з яких багато таких, що не тільки основані на простих розрахунках, але й потребують значну аналітичну і комп’ютерну бази.
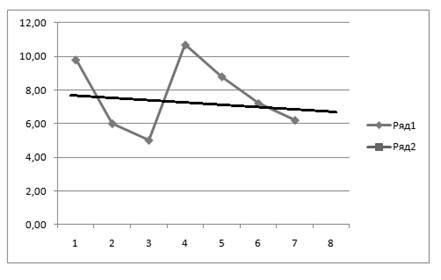
Рисунок 3.6 – Порівняльні результати прогнозу методом проектування тренда
Для складання середньострокових та довгострокових прогнозів застосовуються казуальні та якісні методи, які значно складніші наведених вище методів аналізу часових рядів.
Питання для самоперевірки
- Що називається часовим рядом? Назвіть приклади часових рядів в природі і навколишньому середовищі.
- З яких частин (компонент) складається часовий ряд?
- Які методи аналізу часових рядів Ви знаєте?
- Назвіть різницю між сезонними та циклічними складовими часового ряду.
- В чому полягає ідея реалізації прогнозування за допомогою методу середнього ковзного?
- На які 2 види поділяють метод ковзного середнього? Яка між ними різниця?
- Як здійснюється прогнозування за допомогою методу ковзного середнього?
- Як здійснюється прогнозування за допомогою методу зваженого ковзного середнього?
- В чому полягає ідея реалізації прогнозування за допомогою методу експоненціального згладжування?
- Що таке коефіцієнт α? Назвіть методи вибору коефіцієнта α.
- Як здійснюється прогнозування за допомогою методу експоненціального згладжування?
- В чому полягає основна ідея реалізації прогнозування за допомогою методу проеціювання тренда?
- Як здійснюється прогнозування за допомогою методу проеціювання тренда?
