РОЗДІЛ 4 КОРЕЛЯЦІЙНИЙ АНАЛІЗ ЧАСОВИХ
4.1 Види залежності між величинами
Величини, що характеризують різні властивості об'єктів, можуть бути незалежними або взаємопозв'язаними. Розрізняють два види залежності між величинами (чинниками): функціональну і статистичну.
При функціональній залежності двох величин, значенню однієї з них обов'язково відповідає одне або декілька точно визначених значень іншої величини. Їх застосування допустиме тоді, коли відповідна величина в основному залежить від відповідних чинників.
Статистичною називають залежність, при якій зміна однієї з величин викликає зміну розподілу інших (іншої), і ці інші величини набувають деяких значень з певною вірогідністю.
Окремим випадком статистичної залежності є кореляційна залежність (correlation), яка характеризує взаємозв'язок значень одних випадкових величин з середнім значенням інших, хоча у кожному окремому випадку будь-яка взаємопозв'язана величина може набувати різних значень.
Коефіцієнт кореляції характеризує наявність тільки лінійного зв'язку між ознаками, що позначаються, як правило, символами X і Y. Формула розрахунку коефіцієнта кореляції побудована таким чином, що, якщо зв'язок між ознаками має лінійний характер, коефіцієнт Пірсона точно встановлює тісноту цього зв'язку. Тому він називається також коефіцієнтом лінійної кореляції Пірсона. Якщо ж зв'язок між змінними X і Y не лінійний, то Пірсон запропонував для оцінки тісноти цього зв'язку так назване кореляційне відношення.
Величина коефіцієнта лінійної кореляції Пірсона не може перевищувати +1 і бути меншою ніж -1. Ці два числа +1 і -1 є границями для коефіцієнта кореляції. Коли при розрахунку виходить величина більша +1 або менша -1 – це означає, що допущена помилка в обчисленнях.
4.2 Основні кореляційні показники
Кореляційна залежність визначається різними параметрами, серед яких найбільше поширення набули показники, що характеризують взаємозв'язок двох випадкових величин (парні показники): кореляційний момент, коефіцієнт кореляції. Крім того, можна згадати про інші статистичні показники: математичне сподівання (expectation value), дисперсію (variance), середньоквадратичне відхилення (mean-square estimate) тощо. Розглянемо детальніше дані показники кореляційного аналізу [9, 10].
Математичне сподівання є середнім значенням статистичної вибірки і позначається μ(х). Для дискретної випадкової величини математичне сподівання визначають за формулою:
Дисперсія – це міра розкиду даної величини, тобто її відхилення від математичного сподівання. Позначається в літературі D(х) або var (х) (англ. variance) і визначається за формулою:
Квадратний корінь з дисперсії σ називається середньоквадратичним відхиленням або стандартним розкидом.
Оцінка кореляційного моменту (коефіцієнта коваріації) двох варіант xj і xk обчислюється за початковою матрицею Х
Коефіцієнт коваріації rjk нормованих випадкових величин називають коефіцієнтом кореляції, його оцінка обраховується таким чином:
Значення коефіцієнта кореляції лежить в межах від -1 до +1. Якщо випадкові величини Uj і Uk незалежні, то коефіцієнт rjk обов'язково дорівнює нулю, але обернене твердження неправильне. Коефіцієнт rjk характеризує значущість лінійного зв'язку між параметрами, тобто:
– при rjk =1 значення uij і uik повністю збігаються, тобто значення параметрів набувають однакових значень;
– при rjk = - 1 величини uij і uik набувають протилежних значень. В цьому випадку має місце функціональна залежність;
– при rjk = 0 величини uij і uik практично не позв'язані одна з одною лінійним співвідношенням;
– при | rjk | > 0 і | rjk | < 1 однозначного лінійного зв'язку величин uij і uik немає.
Знак коефіцієнта кореляції дуже важливий для інтерпретації отриманого зв'язку. Підкреслимо ще раз, що якщо знак коефіцієнта лінійної кореляції плюс, то зв'язок між ознаками, що корелюють, такий, що більшій величині однієї ознаки (змінної) відповідає більша величина іншої ознаки (іншої змінної). Іншими словами, якщо один показник (змінна) збільшується, то відповідно збільшується й інший показник (змінна). Така залежність називається прямо пропорційною залежністю.
Якщо ж отриманий знак мінус, то більшій величині однієї ознаки відповідає менша величина іншої. Інакше кажучи, при наявності знака мінус збільшенню однієї змінної (ознаки, значення) відповідає зменшення іншої змінної. Така залежність називається обернено пропорційною залежністю.
4.3 Види кореляційного зв'язку
Задача кореляційного аналізу зводиться до встановлення напрямку (додатного або від’ємного) і форми (лінійного, нелінійного) зв'язку між варіюючими ознаками, вимірювання їх щільності, і, нарешті, до перевірки рівня значимості отриманих коефіцієнтів кореляції [10].
Кореляційні зв'язки розрізняються за формою, напрямком і ступенем (сили).
За формою кореляційний зв'язок може бути прямолінійним або криволінійним. Прямолінійним може бути, наприклад, зв'язок між кількістю тренувань на тренажері і кількістю правильно розв'язуваних задач у контрольній сесії. Криволінійним може бути, наприклад, зв'язок між рівнем мотивації й ефективністю виконання задачі. При підвищенні мотивації ефективність виконання задачі спочатку зростає, потім досягається оптимальний рівень мотивації, якому відповідає максимальна ефективність виконання задачі; подальше підвищення мотивації супроводжується вже зниженням ефективності.
За напрямком кореляційний зв'язок може бути додатний ("прямий") і від’ємний ("зворотний"). При додатній прямолінійній кореляції більш високим значенням однієї ознаки відповідають більш високі значення іншої, а більш низьким значенням однієї ознаки – низькі значення іншої. При негативній кореляції співвідношення обернені. При позитивній кореляції коефіцієнт кореляції має додатний знак, наприклад r = +0,207, при негативній кореляції – від’ємний знак, наприклад r = -0,207.
Ступінь, сила або щільність кореляційного зв'язку визначається за величиною коефіцієнта кореляції.
Сила зв'язку не залежить від її спрямованості і визначається за абсолютним значенням коефіцієнта кореляції.
Максимальне можливе абсолютне значення коефіцієнта кореляції дорівнює r = 1,00; мінімальне r = 0,00.
Загальна класифікація кореляційних зв'язків полягає в такому:
сильний, або щільний, при коефіцієнті кореляції r > 0,70;
середній при 0,50 < r < 0,69;
помірний при 0,30 < r < 0,49;
слабкий при 0,20 < r < 0,29;
дуже слабкий при r < 0,19.
Наведемо формули для розрахунку коефіцієнта кореляції:
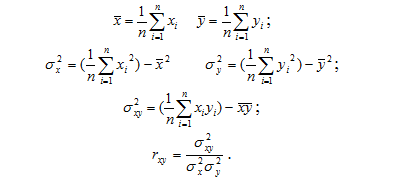
4.4 Гіпотеза про значущість оцінки коефіцієнта кореляції
Необхідно оцінити значущість вибіркової величини коефіцієнта rjk або, відповідно до постановки задачі перевірки статистичних гіпотез, перевірити гіпотезу про рівність нулю коефіцієнта кореляції rjk.
Якщо гіпотеза Н0 про рівність нулю коефіцієнта кореляції буде відкинута, то вибірковий коефіцієнт значущий, а відповідні величини пов'язані лінійним співвідношенням. Якщо гіпотеза Н0 буде прийнята, то оцінка коефіцієнта незначуща, і величини лінійно не пов'язані одна з одною [9 – 11]. Як критерій перевірки нульової гіпотези Н0 застосовують випадкову величину
.Якщо модуль коефіцієнта кореляції відносно далекий від одиниці, то величина t при справедливості нульової гіпотези розподілена за законом Стьюдента з (n – 2) ступенями свободи. Перевірка гіпотези Н0 про рівність нулю коефіцієнта кореляції двовимірної нормально розподіленої випадкової величини здійснюється в такій послідовності:
- обчислюється значення статистики t;
- при рівні значущості α для двосторонньої області визначається критична точка розподілу Стьюдента , яка дорівнює tкр(n - 2; α );
- порівнюється значення t з критичним значенням tкр(n - 2; α). Якщо t < tкр(n - 2; α ), то немає підстав відкидати нульову гіпотезу, в іншому випадку – гіпотеза Н0 відкидається (тобто коефіцієнт кореляції значущий).
Таким чином, постановка задачі лінійного кореляційного аналізу формулюється в такому вигляді.
Є матриця спостережень вигляду:
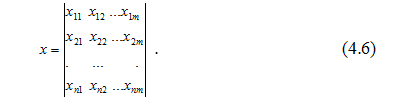
Задача полягає в тому, щоб визначити оцінки коефіцієнтів кореляції для всіх або тільки для заданих пар параметрів і оцінити їх значущість. Незначущі оцінки прирівнюються до нуля.
Задача кореляційного аналізу розв'язується у декілька етапів:
1. Проводиться стандартизація початкової матриці;
2. Обчислюються парні оцінки коефіцієнтів кореляції;
3. Перевіряється значущість оцінок коефіцієнтів кореляції, незначущі оцінки прирівнюються до нуля. За результатами перевірки робиться висновок про наявність зв'язків між варіантами (чинниками).
4.5 Гіпотеза про перевірку нормального розподілу вибірки за критерієм Пірсона
Залежно від розміру початкової вибірки існують різноманітні критерії перевірки закону розподілу випадкового процесу: критерій Колмогорова, критерій ω2 , критерій χ2 тощо. Наведемо метод Пірсона для перевірки часового ряду на нормальність.
Послідовність перевірки узгодження емпіричного розподілу з теоретичним така. Формулюють гіпотезу щодо обраної теоретичної моделі. Згідно з рекомендаціями обирають критерій, задають рівень значущості α, за яким проводять перевірку.
Для цього рівня значущості встановлюють відповідну критичну область критерію перевірки, тобто відповідний квантиль чи квантилі (для двосторонньої області).
Якщо обраний критерій параметричний, невідомі параметри теоретичного розподілу обчислюють за результатами вимірювань. Далі знаходять відповідне значення критерію і перевіряють, чи потрапляє воно в критичну область. Якщо це так, то гіпотезу відкидають. Якщо ні, гіпотезу приймають [38].
В даній роботі для того, щоб перевірити, чи відповідає емпіричний закон розподілу нормальному, використовується критерій χ2.
Його застосування включає в себе такі етапи:
Для групування обчислюють розмах вибірки хn – х1 і вибирають кількість інтервалів r з рекомендацій (n = 200; r =18…20; n = 400; r = 25…30; n = 1000; r = 35…40). І обчислюють ширину інтервалу: 
Результати вимірювань групують за інтервалами, обчислюють частоти mj значень xj , що потрапляють в j-інтервали.
- Обчислюють середнє та вибіркове СКВ:
- Обчислюють значення
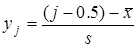та розраховують значення функції теоретичного розподілу – нормального закону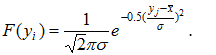 
- Далі обчислюють ймовірність Pj , що відповідає j-му інтервалу:
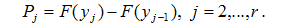
- Останнім визначають критерій перевірки:
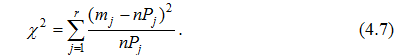
Для обраного рівня значущості α з таблиці для даного χ2-розподілу знаходять відповідне значення (χ*)2 для числа ступенів свободи k = r-l-1, де l – кількість параметрів функції теоретичного розподілу (для нормального закону l = 1). Якщо χ2 < (χ*)2 , гіпотезу приймають, якщо χ2 > (χ*)2 – відкидають.
4.6 Застосування коефіцієнта кореляції при моделюванні ринкових ситуацій
Багато розробників торговельних систем не оцінюють статистичну значимість результатів оптимізації. Це досить неприйнятно, враховуючи, що статистика принципово важлива при оцінці поводження торгівельних систем.
Як, наприклад, можна судити про причину успіху системи – реальний він чи заснований на артефакті або на вдалій вибірці даних? Серед методів статистичного аналізу, найбільш корисних трейдеру, можна назвати перевірку за критерієм Стьюдента, кореляційний аналіз і деякі види непараметричного статистичного аналізу.
Кореляційний аналіздопомагає визначити ступінь взаємозв'язку двох різних змінних. При використанні для прийняття рішень він також допомагає визначити, чи є зв'язки статистично важливими або просто випадковими. За допомогою таких методів можна визначити „довірчі граничні інтервали” реальної кореляції, тобто кореляції по вибірці даних за деякий період часу.
Кореляційна статистика важлива при пошуку змінних, які можна використовувати як прогностичні показники, наприклад, у нейронній мережі або в системі рівнянь регресії.
Наприклад, чи дійсно вигідні угоди йдуть у виді смуг або груп, між якими суцільні збитки? Критерії наявності смуг дозволяють визначити, що ж насправді відбувається. Якщо в системі є серійна кореляція, її можна використовувати для перенастроювання системи.
Наприклад, якщо в системі виражені періоди прибутків і збитків, можна розробити метасистему, що буде проводити угоду за угодою, поки є прибуток, і припиняти торгівлю після першої збиткової угоди, ідучи у віртуальну торгівлю до настання нової прибуткової смуги. Якщо смуги реально існують, то подібна стратегія може значно поліпшити поводження (поведінку) системи.
Питання для самоперевірки
- Які існують види залежностей між величинами?
- Яка різниця між різними видами залежностей між величинами?
- Дайте означення кореляційної залежності між величинами.
- Сформулюйте постановку задачі кореляційного аналізу.
- Назвіть основні етапи проведення кореляційного аналізу.
- Назвіть основні показники статистичної обробки даних та кореляційного аналізу. Наведіть їх розрахункові формули.
- Що характеризує кореляційний коефіцієнт?
- Які висновки про величини можна зробити на основі його значення?
- В чому полягає основна ідея гіпотези про значимість оцінки коефіцієнта кореляції?
- В чому полягає гіпотеза про перевірку нормального розподілу вибірки за критерієм Пірсона?
- Які ще способи для перевірки нормальності вибірки Ви знаєте?
