РОЗДІЛ 5 ОСНОВИ РЕГРЕСІЙНОГО АНАЛІЗУ

5.1  Види залежностей: регресійна залежність

Метою будь-якого дослідження, що здійснюється в даний час, є використання його результатів в майбутньому, або, інакше кажучи, прогнозування стану явища, що вивчається. Приклади такого прогнозування наведені в підручниках всіх природничо-наукових і економічних дисциплін. При цьому, бажаючи вивчати явище у взаємозв'язку з іншими явищами або величинами, доводиться виділяти деякі з них, що впливають на те, що вивчається, оцінювати міру і «якість» впливу, тобто характер зв'язку між тим, що вивчається (основним в даному дослідженні) і величинами якісного або кількісного характеру, що впливають на нього [9].
Надалі «основну», таку, що вивчається, величину називатимемо залежною змінною і позначатимемо літерою Y, інші, впливаючі на Y, величини називатимемо незалежними змінними і позначатимемо літерами x1, x2, …, xk.  Як Y, так іx1, x2, …, xk, вважатимемо числовими.
Розрізняють два види зв'язків.
Якщо значення залежної змінної стає відомим, як тільки відомі значення незалежних змінних, то зв'язок є динамічним або функціональним, оскільки в цьому випадку існує закон, за яким обчислюється Y залежно від x1, x2, …, xk, Y = f(x1, x2, …, xk).  Приклади таких зв'язків: закон вільного падіння тіла; закон Ома; закон Бойля - Маріотта; зв'язок між вартістю одиниці товару і ціною, сплаченою за його партію; залежність продуктивності праці і витрат робочого часу.
Зовсім інакше, коли за значеннями незалежних величин можна встановити лише деяку «середню» тенденцію в значеннях залежної змінної. Так, наприклад, зрозуміло, що між зростанням людини і її вагою існує залежність, створені таблиці такої залежності, що враховують ще зріст, і вік, проте користуватися ними можна лише, знову ж таки, «в середньому». Подібного роду зв'язки називають кореляційними (від лат. слова correlatio – співвідношення), а задачею встановлення математичної форми кореляційного зв'язку займається регресійний аналіз. Залежна змінна в при цьому розглядається як випадкова величина, а незалежні змінні можна прямо або опосередковано контролювати. Кореляційний аналіз вивчає спільний розподіл всіх змінних, що вимірюються з аналізом точності оцінювання одних величин через інші.
На відміну від функціонального зв'язку в регресійному аналізі йдеться про встановлення функції регресії M(y/ x1, x2, …, xk) = f(x1, x2, …, xk) де символ M (·/·) позначає математичне сподівання випадкової величини при заданих значеннях незалежних змінних.
Оскільки незалежні змінні x1, x2, …, xk є контрольованими та керованими, а Y – випадковою величиною, то за даними експерименту, в якому x1, x2, …, xk набули конкретних значень, можна судити лише про оцінку параметра, пов'язаного з розподілом Y. А оцінок же, як правило, можна побудувати багато.
З точки зору подальших використань бажано мати оцінку якомога простішого вигляду і яка задовольняла б деякий критерій оптимальності (подібний до незміщеності, наприклад, для оцінок параметрів).
Із всіх елементарних функцій (виключаючи константу) найбільш простою є лінійна, цей випадок розглянемо надалі детально, як найбільш прозорий з ідейної точки зору і такий, що в той же час дає можливість для подальших узагальнень.

5.2   Лінійна регресія і метод найменших квадратів

Опишемо спочатку математичну постановку завдання, вважаючи, що вивчається одна залежна змінна y, що залежить від однієї незалежної змінної х (так зване завдання парної регресії).
Нехай залежність між х і yмає вигляд:

де– постійні коефіцієнти, що називаються параметрами моделі; e – випадкова величина з математичним сподіванням 0 і дисперсією s2 .
В цьому випадку рівняння регресії перетворюється на рівняння прямої

Передбачимо, що незалежна змінна набула значень x1, x2, …, xn, внаслідок чого залежна змінна набула значень y1, y2, …, yn. У припущенні лінійної залежності отримуємо n рівностей

де   ei– незалежні і розподілені так само, як e.

Потрібно за значеннями пар (xi, yi) оцінити невідомі Як ми вже знаємо, кожне завдання оцінювання пов'язане з деяким критерієм якості. У теорії, що викладається нами, таким критерієм є критерій найменших квадратів:

Запишемо цю суму інакше, так, щоб була помітна залежність від

Тепер остаточно приходимо до такої задачі: знайти такі значення невідомих параметрівщоб функція

набула найменшого значення.
Метод розв’язання цієї задачі відомий з курсу вищої математики. Знаходимо часткові похідні функції Q і прирівнюємо їх до нуля, внаслідок чого приходимо до системи лінійних рівнянь:

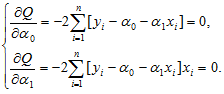
Після очевидних перетворень отримуємо систему:

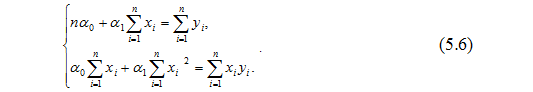
Позначимо вибіркові середні

У цих позначеннях після ділення кожного рівняння системи на n вона набуде вигляду:

а її рішення (шукані оцінки коефіцієнтів рівняння регресії) буде таким:

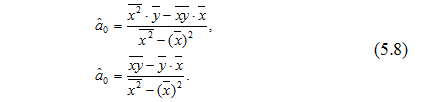
Якщо ввести ще позначення і перетворити вираз

то оцінка функції регресії набуде такого вигляду:

Приклад 1. Агент з продажу будинків вивчає залежність між ціною будинку y (в $ 1000) і загальною його площею х (у сотнях квадратних футів). З цією метою він склав вибірку з 15 будинків і зафіксував такі результати:

Таблиця 5.1 – Тестова вибірка

i

xi

yi

i

xi

yi

1

20.0

89.5

9

24.3

119.9

2

14.8

79.9

10

20.2

87.6

3

20.5

83.1

11

22.0

112.6

4

12.5

56.9

12

19.0

120.8

5

18.0

66.6

13

12.3

78.5

6

14.3

82.5

14

14.0

74.3

7

27.5

126.3

15

16.7

74.8

8

16.5

79.3

 

 

 

Позначивши пари (xi, yi) на координатній площині, він отримує так звану кореляційну хмару, вигляд якої дозволяє передбачити, що наявна лінійна залежність між змінними. Вона наведена на рис. 5.1.

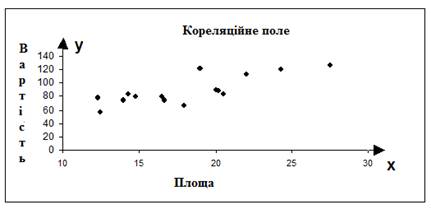
Рисунок 5.1 – Кореляційне поле

Прийнявши цю гіпотезу, він обчислює

а потім за отриманими вище формулами оцінки:

Тепер пряма регресії описується рівнянням:

Її графік нанесемо на кореляційне поле (рис. 5.2):

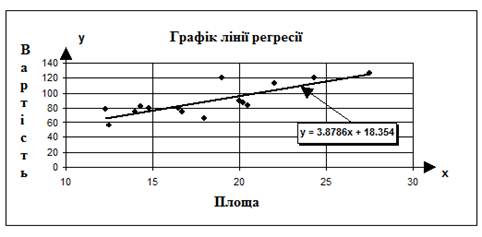
Рисунок 5.2 – Регресійне рівняння

5.3    Множинна регресія і етапи її побудови

Регресія називається множинною, якщо вона відображає залежність результативної ознаки від декількох чинників [10, 12].
Побудова моделей множинної регресії включає декілька етапів:
•  вибір форми зв'язку (рівняння регресії);
•  відбір факторних ознак;
•  забезпечення достатнього об'єму сукупності для отримання незміщених оцінок.
Розглянемо детальніше кожен з них.
Дані, які збираються для проведення регресійного аналізу, зазвичай є “історичними ” фактами, тобто це числа, які показують значення будь-якого з чинників в будь-якому з попередніх періодів часу або географічних районів. Вони використовуються для розрахунку оцінок коефіцієнтів регресії і визначення міри відповідності моделі відповідної дійсності змінам результативної ознаки.

Для досягнення цих цілей можна застосовувати різні методи, але найбільш універсальним і найчастіше використовуваним є метод найменших квадратів, описаний вище:

Вибрати форми зв'язку іноді важко, тому що, використовуючи математичний апарат, теоретично залежність між ознаками  може  бути виражен великим числом різних функцій. Для будь-якої  форми залежності вибирається цілий  ряд рівнянь, які певною мірою описуватимуть ці зв'язки.
Найбільш прийнятним способом визначення вигляду вихідного рівняння регресії є метод перебору різних рівнянь.
Суть даного методу полягає в тому, що велике число рівнянь (моделей) регресії, відібраних для описування зв'язків якого-небудь соціально-економічного явища або процесу, реалізується на ЕОМ за допомогою спеціальний розробленого алгоритму перебору з подальшою статистичною перевіркою, головним чином на основі t-критерію Стьюдeнта і  F-критерію Фішера. Хоча з іншого боку, спосіб перебору є досить трудомістким і пов'язаний з великим об'ємом обчислювальних робіт.
Важливим етапом  побудови вже  вибраного рівняння множинної регресії є відбір і подальше включення факторних ознак. Складність формування рівняння множинної регресії полягає в тому, що майже всі факторні ознаки залежать одна від одної. Проблема розмірності моделі зв'язку, тобто визначення оптимального  числа факторних ознак, є однією з основних проблем побудови множинного рівняння регресії. З одного боку, чим більше факторних ознак включено в рівняння, тим  воно краще описує  явище.  Проте модель розмірністю 100 і більше  факторних  ознак складно реалізовується і потребує великих витрат машинного часу. Скорочення розмірності  моделі  за рахунок виключення другорядних, економічно і статистично неістотних чинників сприяє простоті і якості її реалізації.  В той же час побудова моделі регресії малої розмірності може призвести до того, що така модель буде недостатньо адекватна досліджуваним явищам і процесам.
Найбільш  прийнятним способом  відбору  факторних  ознак є крокова регресія (кроковий регресійний аналіз). Суть методу крокової регресії полягає в  послідовному  включенні чинників в рівняння регресії і подальшій перевірці їх значущості. Чинники по черзі вводяться в  рівняння  так званим "прямим методом". При перевірці значущості введеного чинника визначається,  наскільки  зменшується сума квадратів залишків і збільшується величина множинного коефіцієнта кореляції. Одночасно використовується і зворотний метод, тобто виключення чинників, що стали незначущими на основі t-критерію Стьюдента. Чинник є незначущим, якщо його включення в рівняння регресії лише змінює значення коефіцієнтів регресії, не зменшуючи суми квадратів залишків і не збільшуючи їх значення. Якщо при  включенні в модель відповідної факторної ознаки величина множинного коефіцієнта кореляції збільшується, а коефіцієнт  регресії не змінюється (або змінюється неістотно), то дана ознака суттєва і його включення в рівняння регресії необхідно [13].
Якщо ж при включенні в модель факторної ознаки коефіцієнти регресії змінюють не лише величину, але і знаки, а множинний коефіцієнт кореляції  не зростає, то дана факторна ознака визнається недоцільною для включення в модель зв'язку.
Розглянемо побудову множинної регресії на вищенаведеному прикладі. Відомо, що на частку ринку, яка зайнята нерухомістю, окрім ціни впливають і інші чинники А оскільки майже всі проблеми в маркетингу включають у себе декілька різних чинників, то в більшості випадків слід застосовувати моделі множинної регресії.
Концепції і методи, які використовуються в множинному регресійному аналізі, практично ті ж самі, але з деякими модифікаціями і доповненнями, пов'язаними з вивченням декількох чинників одночасно.
Створення моделі множинної регресії пов'язане також з додатковою складністю. Перш за все, неможливо досліджувати взаємозв'язок за допомогою діаграми розсіювання. Її, звичайно, можна використовувати для відображення взаємозв'язку результативної ознаки і будь-якого з незалежних чинників по черзі.
Але не слід забувати, що отримана в такий спосіб інформація має обмежене значення, оскільки незалежні змінні часто впливають одна на одну так само, як і на результативну ознаку.
Розглянемо зразок знаходження моделі множинної регресії з двома змінними виду:

Розв’язання задачі полягає в тому, щоб знайти невідомі b0, b1,b2 . Це можна зробити, розв’язавши систему трьох лінійних рівнянь з трьома невідомими b0, b1,b2:

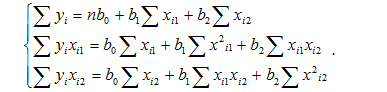
Для розв’язання системи можна також скористатися методом Крамера або формулами:

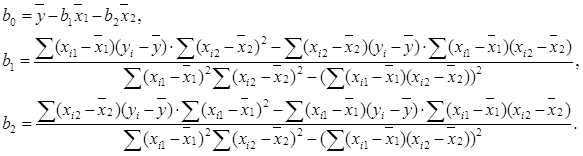
Розглянемо етапи проведення регресійного аналізу:
– побудова системи факторів, що істотно впливають на результативну ознаку;
– розроблення моделі, яка відображає загальний зміст взаємозв'язків, що вивчаються, і кількісне оцінення її параметрів;
– перевірка якості моделі;
– оцінення впливу окремих факторів.
На першому етапі здійснюється добір факторів, що істотно впливають на результативну ознаку. Він проводиться, насамперед, виходячи зі змістовного аналізу. Для одержання надійних оцінок у модель не слід включати багато факторів, їхня кількість не повинна перевищувати однієї третини обсягу даних, що аналізуються.
Але оскільки на початковому етапі розробки моделі в дослідника немає однозначної відповіді на питання щодо набору істотних факторів, то при використанні ЕОМ вибір факторів звичайно здійснюється безпосередньо в процесі створення моделі методом послідовної регресії. Суть цього методу полягає в послідовному включенні додаткових факторів у модель і оціненні впливу доданого фактора.
Використовується також підхід, за яким на фактори, що включаються до попереднього складу моделі, не накладається особливих обмежень і лише на наступних стадіях проводиться їхнє оцінювання і вибір.
Другий етап починається з розробки моделі, що відображає загальний зміст взаємозв'язків, що вивчаються.
Регресійна модель — це рівняння (або система рівнянь), що показує, які фактори, на думку дослідника, підлягають аналізу з точки зору взаємозв'язків.
Регресійне рівняння дає також уявлення про форму зв'язку. Класифікацію регресійних рівнянь можна подати у виді схеми на рис. 5.3.
Регресія називається парною, якщо вона відображає залежність між результативною ознакою й одним фактором.
Регресія називається множинною, якщо вона відображає залежність результативної ознаки від декількох факторів.
Якщо залежності лінійні щодо параметрів (але не обов'язково лінійні щодо незалежних змінних), то регресія називається лінійною. У іншому випадку регресію називають нелінійною.

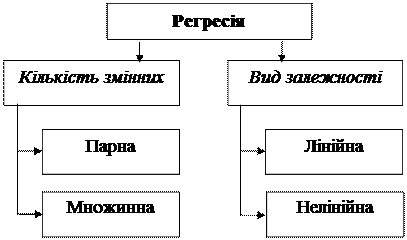
Рисунок 5.3 – Класифікація регресійної залежності

Наступний крок після вибору змінних і способу їхнього подання – визначення форми рівняння регресії. В основу виявлення і встановлення аналітичної форми зв'язку покладене використання певних математичних функцій – лінійної, логарифмічної, ступеневої, експоненціальної, поліноміальної і деяких інших.
Практично для обчислення параметрів функцій застосовуються спеціальні комп'ютерні програми, серед яких найбільші можливості для тлумачення результатів користувачеві надають програми лінійного регресійного аналізу. Тому більшість аналітиків віддають перевагу саме йому.
Дані, що збираються для проведення регресійного аналізу, звичайно являють собою “історичні зведення”, тобто цифри, що показують значення кожного з факторів у кожному з попередніх періодів часу або географічних районів. Вони використовуються для одержання оцінок коефіцієнтів регресії і визначення ступеня відповідності моделі змінам результативної ознаки.
Для досягнення цих цілей можна застосовувати різні методи, але найбільш універсальним і найбільш частим у використанні є метод найменших квадратів. Оцінки за методом найменших квадратів – це ті величини коефіцієнтів регресійного рівняння, що мінімізують суму квадратів відхилень значень результативної ознаки, що спостерігаються дійсно, (Yi) від тих значень, що одержують з рівняння Y(Xi).
Для оцінення якості моделі і повноти набору пояснювальних факторів звичайно використовують коефіцієнт детермінованості R2. Його ще називають величиною вірогідності апроксимації або рівнем надійності. Коефіцієнт детермінування R2 – це відношення дисперсії, що пояснюються регресійним аналізом, до загальної дисперсії [13].
Коефіцієнт детермінації дає кількісну оцінку міри аналізованого зв'язку. Він показує частину варіації результативної ознаки, яка знаходиться під впливом факторів, що вивчаються, тобто визначає, яка частка варіації ознаки Y враховується в моделі й обумовлена впливом на неї незалежних факторів.
Чим ближче R2 до 1, тим точніше рівняння регресії пояснює фактор, що вивчається (при функціональному зв'язку R2 дорівнює 1, а через відсутність зв'язку – 0).

Питання для самоперевірки

  1. Сформулюйте постановку задачі регресійного аналізу.
  2. Назвіть основні етапи проведення регресійного аналізу та припущення.
  3. Що таке рівняння регресії і який воно має вигляд?
  4. Поясніть методику вибору рівняння регресії.
  5. Як розраховуються коефіцієнти рівняння регресії?
  6. Як оцінюється якість отриманого рівняння регресії?