2.МОДЕЛЮВАННЯ ЗАДАЧ СИСТЕМНОГО АНАЛІЗУ

Людина як у побутовій, так і службовій областях своєї діяльності постійно стикається з різними задачами аналізу, за результатами якого приймає рішення з точки зору керування системами. Прийняті рішення відрізняються як за ступенем відповідальності, так і за ступенем значимості наслідків. Різними аспектами проблем, що пов'язані з прийняттям управлінських рішень, з «оптимальною» поведінкою людей, з перетинанням інтересів кількох сторін, займаються багато наук, наприклад, таких, як дослідження операцій, дискретна математика, економіка, соціологія, право та ін.
На відміну від інших, системний аналіз аналізує ці проблеми за допомогою математичного апарату. Це означає, що хоча б деякі дані, що фігурують у формулюванні задачі, повинні мати кількісні значення. Якісні дані (умови) досліджуваної проблеми враховуються додатково і є своєрідним фоном для використання математичних моделей.
Як відомо, у загальному випадку прийняття рішень потребує наявності:

  • особи (осіб), що приймають рішення (ОПР);
  • мети прийняття рішення;
  • варіантів вибору рішення (множина допустимих рішень).

При цьому, слід мати на увазі і те, що рішення приймаються з урахуванням певної обстановки, умов, що її супроводжує, і передумов.
Все це ті головні фактори, що характерні для будь-якої задачі прийняття рішень, і які обов'язково повинні бути відображені у математичній моделі.
Мета ОПР - з урахуванням існуючих умов прийняти те рішення з множини допустимих у даній ситуації рішень, що якнайкраще сприяє досягненню поставленої мети (оптимальне рішення).
Невід'ємною частиною методології системного аналізу є всебічний якісний і кількісний аналіз проблеми, що передує її математичному моделюванню. Тому говорять про системний аналіз проблеми, що припускає виконання таких компонентів:
- доматематичний (змістовний) аналіз проблеми;
- математичний аналіз проблеми;
- застосування результатів дослідження на практиці.
Проведення такого аналізу для кожної конкретної задачі повинно здійснюватися операційною групою, що включає фахівців даної області (постановників проблем, замовників), математиків, економістів, юристів, соціо­логів та ін. При цьому як не існує універсальних методів побудови математичних моделей, так і не існує універсальних методик і керівних принципів системного аналізу. Кожне окреме дослідження має свої особливості. Тому можна рекомендувати лише деякі, досить загальні принципи та етапи, що включають:
1) змістовну постановку задачі;
2) формулювання проблеми та визначення мети системного аналізу;
3) збирання даних (статистичних, експертних і ін.);
4) побудову моделі досліджуваної системи;
5) пошук і розроблення методу розв’язування задачі за допомогою моделі;
6) перевірку математичної моделі та оцінювання рішення;
7) реалізацію результатів на практиці.
Етапи 1-4 відносяться до доматематичної частини аналізу і виконуються фахівцями тієї області, до якої належить досліджувані системи. Дуже важливо, щоб перед математичним моделюванням об'єкт дослідження (предметна область) був досконально вивчений самими постановниками (замовниками). Зокрема, дослідникам повинні бути вичерпно надані усі необхідні документальні і статистичні дані. Збирання статистичних даних або іншої інформації - не справа математиків, їх справа полягає в організації збереження, аналізу і оброблення даних, наданих їм замовниками у зручній формі.
Етапи 5 і 6 відносяться до математичної частини аналізу. Це найскладніші і ключові етапи системного аналізу.
Етап 7 – є заключною частиною системного аналізу і здійснюється спільними зусиллями замовників і аналітиків-розробників моделі.
Поговоримо про кожен з цих етапів. При цьому будемо виділяти найскладніші у розумінні етапи і намагатися засвоїти методи їх здійснення на конкретних прикладах. Однак вже зараз відзначимо, що у кожному конкретному випадку етапи системного аналізу мають різну питому вагу у загальному обсязі робіт з точки зору часових, витратних і інтелектуальних показників. Дуже часто важко провести чіткі межі між ними і вказати, де закінчується даний етап і починається наступний.

2.1 Змістовна постановка задачі моделювання

Вище вже вказувалось, що у постановці задачі системного аналізу обов'язкова участь двох сторін: замовника (ОПР) і виконавця системного проекту. При цьому участь замовника не обмежується фінансуванням роботи – він повинен (для користі справи) зробити аналіз системи, якою він керує, сформулювати цілі та обговорити можливі варіанти дій відповідно до прийнятих рішень. Так, наприклад, у згаданому вище прикладі системи керування навчальним процесом, однією з причин її невдалого завершення було те, що одна з підсистем керівництва практично не мала свободи дій щодо підсистеми тих, кого вони навчали.
Очевидно, що на цьому етапі повинні бути встановлені і зафіксовані поняття ефективності діяльності системи. При цьому відповідно до принципів системного підходу необхідно враховувати максимальне число зв'язків як між елементами системи, так і щодо зовнішнього середовища. Зрозуміло, що виконавець-розробник не завжди може, і не повинен мати професійні знання щодо тих процесів, які мають місце у системі, або принаймні є головними. З іншого боку, обов'язковою є наявність таких знань у замовника, тобто, у керівника або адміністратора системи. Замовник повинен знати що треба зробити, а виконавець, тобто фахівець у галузі системного аналізу, повинен знати як це зробити.
Однак слід відзначити, що їм краще було б навчитися і тому і іншому. Наприклад, якщо ви будете у ролі адміністратора, то до професійних знань доречні знання з області системного аналізу – розумна постановка задачі, з урахуванням технології прийняття рішень на сучасному рівні буде гарантією успіху.
Якщо ж ви будете працювати у іншій категорії, тобто як розробники, то вам не обійтися без «технологічних» знань. Робота щодо системного аналізу у будь-яких системах навряд чи виявиться ефективною без спеціальних знань з області економічної ефективності.

2.2 Загальна структура математичних моделей системного аналізу

Під час визначення елементів математичної моделі будемо виходи­ти з того, що у системному аналізі, у загальному випадку, вивчаються задачі прийняття рішень і, як окремий випадок, задачі оптимізації.
Однією з основних вимог до побудови математичних моделей досліджуваних систем є врахування їх основних факторів. При цьому для виявлення основних елементів моделі слід відповісти на такі запитання:
- Хто приймає рішення ?
- Яка мета прийняття рішення для кожного ОПР ?
- У чому полягає прийняття рішення ?
- Які є можливості ОПР (з точки зору прийняття можливих рішень)?
- За яких умов відбувається прийняття рішення?
Формалізуючи (описуючи математично) відповіді на ці запитання ми отримаємо необхідну модель системного аналізу.
Для з'ясування загальної структури математичних моделей системного аналізу введемо деякі загальні позначення.
Позначимо через  N = {1,2,...,n} множину сторін, що беруть участь у даній конкретній задачі системного аналізу, де кожен елемент множини N називається особою, що приймає рішення (ОПР), наприклад, окрема особистість, фірма, плановий орган великого концерну, уряду та ін. Кожен елемент iÎN характеризується своїми можливостями. Позначимо через Хi множину усіх його допустимих рішень (стратегій, альтернатив). Припустимо, що такі множини математично описані: X1, X2,..., Xn.
Після цього процес прийняття рішення всіма ОПР зводиться до такого формального акту: кожна з ОПР вибирає конкретний елемент x1ÎX1,  x2ÎX2,…,  xnÎXn зі своєї припустимої множини рішень.
У результаті отримується набір х = (x1,...,xn) обраних рішень, що називається ситуацією.
Формалізація цілей прийняття рішення здійснюється за такою схемою. Тим або іншим способом будуються аналітичні закони (функції) f1,..., fn, що ставлять відповідно до кожної ситуації  x набір з  n чисел f1(x),  f2(x),..., fn(x).
Функція fi(x) = fi (x1,...,xn)  називається критерієм якості i-ої ОПР. Число fi(x) є кількісною оцінкою ситуації x для i-oї ОПР з точки зору переслідуваної нею мети. Тому в моделі мета i-oї особи формалізується таким чином: вибрати таке рішення xiÎXi, щоб досягти найбільшого значення функції fi. Однак досягнення цієї мети цілком від нього не залежить з огляду наявності інших сторін, що впливають на загальну ситуацію x з метою досягнення своїх власних цілей. Цей факт перетинання інтересів (конфліктність) пояснюється тим, що функція fi крім xi  залежить і від інших змінних xj (i ¹ j). Тому в моделях прийняття рішення з багатьма учасниками застосовуються складніші принципи оптимальної поведінки, ніж пряма максимізація або мінімізація  критерію якості.
Нарешті, нехай деяким чином (математично) описані всі ті умови, за яких відбувається прийняття рішення. Сукупність усіх цих умов, що виступають у моделі у вигляді певних рівнянь зв'язку, позначимо одним символом Σ. Математично система Σ містить опис зв'язків між керованими і некерованими змінними, опис впливу випадкових факторів, облік динамічних характеристик та ін.
Таким чином, загальна структура задачі прийняття рішення з багатьма учасниками виглядає так:
<N; X1,..., Xn; f1,..., fn; Σ >.                                 (2.1)
Мета математичного моделювання – для поставленої фахівцями конкретної задачі – отримати конкретний опис елементів наведеної структури. Слід відзначити, що математичне моделювання – це дуже складна задача, що потребує від розробників значних трудовитрат, навичок, знань і може бути виконана лише за наявності необхідного обсягу попередньої змістовної інформації.
Підсумовуючи, можна сказати, що основними елементами математичної моделі будь-якої задачі системного аналізу з прийняттям рішень є.
1. Множина ОПР (N).
2. Критерії якості (f1,...,fn).
2. Множина допустимих рішень (X1,...,Xn).
4. Обмеження на параметри задачі, передумови рівняння зв'язку (Σ).
Конкретизуючи ці елементи, їх характеристики і властивості, ми отримуємо той чи інший конкретний клас задач (клас моделей) прийняття рішення. Так, якщо множина N складається тільки з одного елемента (n = 1), а всі умови і передумови вихідної реальної задачі можна описати у вигляді множини допустимих рішень цієї єдиної ОПР, то з вищенаведеного виразу отримаємо структуру задач системного аналізу, зокрема задач оптимізації (екстремальних задач) < Х, f >. У наведеній схемі ОПР може розглядатися як орган планування, множина допустимих рішень Х задається за допомогою обмежень на можливості ОПР, а критерій якості f називається цільовою функцією. При цьому задача аналізу (оптимізації) ставиться таким чином:
         
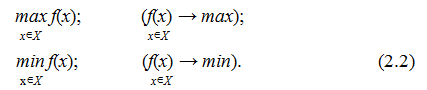
Це різні форми запису однієї і тієї ж задачі. Їх оптимальними розв’язками називаються пари x*, f(x*). У загальному ж випадку, модель досліджуваної системи можна описати у самому лаконічному вигляді, тобто, у вигляді залежності
E = f (X, Y)   (2.3)
де E – деякий кількісний показник (критерій) ефективності з точки зору досягнення деякої мети її функціонування системи;
X – керовані змінні системи, на які ми маємо вплив;
Y – некеровані, тобто зовнішні щодо системи впливи.

2.3 Основні етапи математичного моделювання

Для побудови математичних моделей конкретних задач системного аналізу можна рекомендувати таку послідовність робіт.
1. Вивчення умови задачі (предметної області).
2. Визначення найважливіших факторів.
2. Виділення відомих і невідомих параметрів.
4. Виявлення керованих і некерованих параметрів.
5. Доповнення умови задачі відсутніми відомостями.
6. Введення системи позначень.
7. Побудова математичної моделі задачі (математичний опис най­важливіших факторів, співвідношень і зв'язків між параметрами).
Розглянемо наведені етапи моделювання на конкретних прикладах.
Приклад 2.1. (Планування добового випуску продукції). Процес виготовлення виробів двох видів полягає у послідовному обробленні кожного з них на трьох верстатах. Нам відомі: час експлуатації кожного верстата за добу, час оброблення одиниці кожного виробу на кожному верстаті, вартість реалізації одиниці кожного виробу. Потрібно скласти план добового випуску виробів таким чином, щоб дохід від їх продажу був максимальним.
Під час аналізу найважливіших факторів будемо виходити тільки з умови поставленої задачі, відповідно до яких:
- ОПР – орган планування фірми;
- мета – досягнення максимуму прибутку від продажу випущених за добу виробів двох видів;
- прийняття рішення для ОПР полягає у визначенні добових обсягів випуску кожного з двох видів виробів;
- можливості ОПР обмежені часовими ресурсами експлуатації верстатів трьох видів;
- про інші обмеження або умови у задачі нічого не говориться.
Після виявлення найважливіших факторів слід аналізувати всі параметри задачі: значення яких параметрів відомо (задано); які параметри є невідомими (шуканими) величинами; якими з параметрів ми можемо керувати (керовані змінні), а якими не можемо (некеровані параметри).
У наведеному прикладі відомими є такі параметри:

  • добова норма b1 експлуатації верстата 1;
  • добова норма b2 експлуатації верстата 2;
  • добова норма b3 експлуатації верстата 3;
  • час aij обробки одиниці виробу виду i на верстаті типу j;
  • вартість с1  (продажу) одиниці виробу виду 1;
  • вартість c2 (продажу) одиниці виробу виду 2;

Усі ці параметри є некерованими, оскільки вони задані (їх значення можна знайти в довідниках або нормативах, визначити з минулого досвіду). Шуканими ж є такі величини:
- обсяг добового випуску виробу виду 1;
- обсяг добового випуски виробу виду 2.
Ці два параметри можна вважати керованими, оскільки фірма сама визначає їх величину, виходячи з реальних умов.
Далі для складання математичної моделі задачі потрібно ввести систему позначень невідомих параметрів задачі. Для нашого прикладу зробимо такі позначення:
x1 - обсяг добового випуску одиниць виробу виду 1;
x2 - обсяг добового випуску одиниць виробу виду 2.
Тоді прибуток від продажу x1 і x2 буде визначатися як c1 x1 + c2 x2, а час, що необхідний для оброблення x1, x2 одиниць виробів на верстаті j - як aij x1 + a2j x1 , (j = l, 2, 3).
Тепер поставлену задачу можна сформулювати математично:
  c1 x1 + c2 x2 ® max,
a11 x1 + a21 x2 £ b1,
a12 x1 + a22 x2 £ b1,                             (2.4)
a13 x1 + a23 x2 £ b1,
                                                   x1 ³ 0, x2 ³ 0.
Умови невід’ємності змінних випливають з того, що величини  x1 і x2 - це доповнення моделі відсутньою, однак, очевидною інформацією.
Наведений запис і є задачею математичного програмування з цільовою функцією c1 x1 + c2 x2 і множиною допустимих рішень X, що описується п'ятьма нерівностями (на площині це багатокутник, що утворений перетинанням п'яти півплощин).
У наведених нижче прикладах побудови моделей простежте етапи математичного моделювання, які ми виконаємо без коментарів (див. з цього приводу Приклад 2.1).
Приклад 2.2. (Розміщення замовлень). Фірма отримала замовлення на кілька тисяч нових виробів, що складаються з окремих блоків. Керівництво фірми прийняло рішення розмістити замовлення на виготовлення n блоків і вибрало n фірм-постачальників. Кожне замовлення настільки велике, що фірма-постачальник не може виконати більше одного замовлення. Кожному постачальнику запропоновано визначити вартість виконання замовлення, тобто ціну, за якою він готовий поставити фірмі різні блоки. Фірма повинна укласти n контрактів на постачання їй n видів блоків, мінімізувавши при цьому свої загальні витрати на придбання комплектуючих вузлів зі сторони.
Позначимо: i – номер (назва) блоку, i = 1,....n;  j – номер (назва) фірми-постачальника, j = 1,...,n; сij - вартість виконання i-гo блока j-ої фірми (задане число). Крім того, введемо для кожного i і j число
.          (2.5)
Цільова функція, що має зміст загальних витрат на покупку комплектуючих блоків, запишеться так;
.
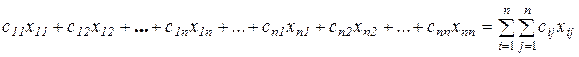(2.6)
Обмеження задачі (на змінні хij) мають такий зміст:
- кожен i-й блок повинен бути виконаний;
- кожен j-й постачальник повинен виконати один який-небудь блок.
Математично ці умови запишуться так:
xi1+xi2 +…+xin =1,  xij + x2j+…+ xnj =1...                          (2.7)
Таким чином, приходимо до такої задачі оптимізації (моделі):
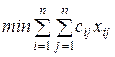;                                             (2.8)
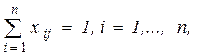
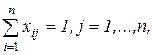  xij = 0 або 1 для всіх i, j.
Приклад 2.3. (Вибір портфеля цінних паперів). Фахівцю з фінансового аналізу, що працює в банку (або в страховій компанії) потрібно визначити найкращий набір акцій, облігацій та інших цінних паперів на виділену суму з метою мінімізації ризику, пов’язаного  з придбанням набору цінних паперів. Прибуток до кінця планового періоду на кожен долар, вкладений у папір j-го виду, характеризується двома показниками: аj – фактичний прибуток (випадкове число), aj – очікуваний прибуток. Потрібно, щоб очікуваний прибуток на долар інвестицій був для всього набору цінних паперів не нижчий заданої величини b.
Для визначення моделі приймемо всі фонди, що виділені для придбання цінних паперів, рівними одиниці і позначимо через xj – частку від усіх фондів, що виділяються для придбання цінних паперів виду j. Ризик враховується за допомогою коваріації sij = М (аi, - ai) (аj - aj) прибутку для цінних паперів виду i і виду j (термін з теорії ймовірностей). Математична модель, при цьому, запишеться як
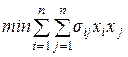                                               (2.9)
за обмежень: 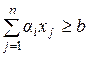;  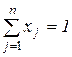;  xj ³ 0, j = 1,…,n
Тут n - число різновидів цінних паперів. Цільова функція має сенс дисперсії фактичного прибутку (розсіювання фактичного прибутку від очікуваного), перше обмеження є умова на очікуваний прибуток, а останнє - не перевищення фондів, виділених на покупку цінних паперів.
Приклад 2.4. (Задача про рекламу). Фірма планує проведення радіорекламної компанії зі збуту автомобілів в одному з регіонів, де розташовано s радіостанцій, протягом двох тижнів. Фірма оцінила попередньо, що якщо радіостанції j виділити уj доларів, то чистий прибуток від збільшення збуту дорівнює Rj(yj) (Rj - функція реалізації прибутку від обсягу фінансування реклами).
На рекламу виділена загальна сума, що дорівнює N доларам. Число рекламних оголошень на день не повинно перевищувати M. Якщо фірма виділила j-ій радіостанції уj доларів, то число рекламних оголошень буде Kj(yj)  (Kj - функція, яка кожній виділеній сумі ставить у відповідність кількість рекламних оголошень на день, і вважається відомою). Як потрібно фінансувати s радіостанцій, щоб отримати сумарний максимальний прибуток від реакції збуту на рекламу? Очевидно, що математична модель буде мати вигляд:
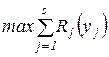                                      (2.10)
за обмежень: 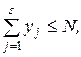 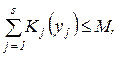  yj ³ 0, j = 1,…,s.
Приклад 2.5. (Задача керування виробництвом). Фірма повинна розробити календарну програму випуску деякого виду виробів на плановий період, що складається з Т відрізків (тижнів, місяців, кварталів, років). Передбачається, що для кожного з цих відрізків є точний прогноз попиту на продукцію, що випускається. Час виготовлення партії виробів настільки малий, що ним можна знехтувати. Для різних відрізків попит неоднаковий, крім того, на економічні показники виробництва впливають обсяги виготовлених партій. Збереження запасів, що виникають при цьому, (перевищення випуску над попитом на деяких відрізках) пов’язано з певними витратами. Потрібно розробити таку програму, за якою загальна сума витрат на виробництво і вартість запасів буде мінімальною за умови повного задоволення попиту на продукцію.
Позначимо через:
xt – випуск продукції протягом деякого відрізка t;
yt – рівень запасів на кінець відрізка t;
Dt – попит на продукцію для відрізка t;
Витрати на відрізку t (позначимо їх через Сt) залежать від випуску xt і рівня запасів yt, тобто є функцією від цих невідомих величин: ct = ct (xt, yt).
Вимога задоволення попиту в межах кожного часового відрізка означає, що рівень запасів на кінець відрізка t (тобто yt) повинен дорівнювати сумі – рівня запасів на початок відрізка t (тобто yt-1) і випуску продукції на відрізку t (тобто xt) мінус попит на відрізку t (тобто Dt).
Звідси отримуємо таку модель
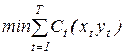                                            (2.11)
за обмежень: уt-1 + xt - yt = Dt,   t =1,2,…T;  yТ = 0,  xt, yt ³ 0 для всіх t.
Тут y0 – заданий рівень запасів на початок планового періоду, а yТ  – рівень запасу на кінець періоду.
Приклад 2.6. (Оптимізація схеми обслуговування). Система обслуговування складається з n типів різних приладів (наприклад, каси в магазинах, телефонні лінії, автозаправні колонки та ін.). Кожен прилад у будь-який момент часу обслуговує не більше однієї заявки (наприклад, покупця, телефонну розмову, автомобіль та ін.). Відома кількість приладів j-го типу і число заявок i-го типу, що прибули в систему на момент часу t. Відома також ефективність j-го приладу під час обслуговування заявки i-го виду. Потрібно розподілити вільні прилади за заявками таким чином, щоб сумарна ефективність була найбільшою.
Для побудови моделі спочатку введемо позначення вільних величин:
Nj - кількість приладів j-го типу;
dit - число заявок i-го типу на момент часу t;
μij - ефективність j-го приладу при обслуговуванні заявки i-го виду.
Позначимо шукану величину через  xij - число приладів j-го виду, відведених для обслуговування заявок i-го типу. Цих даних досить для складання математичної моделі вигляду
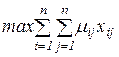                                             (2.12)
за обмежень: 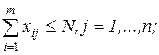 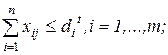  xij - цілі невід’ємні числа для всіх i, j, тут m і n задані числа кількості видів заявок і приладів.
Приклад 2.7.(Вибір оптимального виду посівної культури). Фермер може посіяти одну з трьох культур: A1, А2 або А2. Врожаї цих культур багато в чому залежать від погоди. Потрібно визначити, яку з цих культур сіяти, щоб забезпечити найбільший прибуток, якщо відома ціна аi одного центне­ра культури Ai, i = 1, 2, 3, і середня врожайність кожної культури в залежності від погоди (літо буде посушливим, нормальним або дощової). Достовірний прогноз погоди відсутній.
Позначимо через hij - врожайність i-ої культури за погодних умов j (тут j = 1 – літо посушливе, j = 2 – нормальне літо, j = 3 – дощове літо). Числа hij, як і числа ai  задані (відомі). Реально може мати місце тільки одна із ситуацій (i, j), i = l, 2, 3; j = l, 2, 2. Причому (i, j) означає, що посіяно культуру Aj, а погода знаходиться у стані j. Усього таких ситуацій дев'ять. Очевидно, що ОПР (фермер) може вибрати тільки вид культури, стан погоди від нього не залежить. Якщо фермер засіяв культуру A1, то він може отримати (залежно від стану погоди) один з таких прибутків: a1h11, a1 h12, a1h13, щодо культури A2: a2h21, a2h22, a2h23, і для культури А3: a3h31, a3h32, a3h3 .
Запишемо всі ці результати в одну таблицю (матрицю):
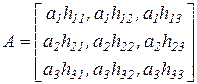.                       (2.13)
Ця матриця і буде математичною моделлю вихідної задачі. У ній дія фермера зводиться до вибору одного з рядків матриці (однієї з трьох стратегій). Його прибуток залежить від «вибору» природою одного зі своїх станів (одного із трьох стовпців матриці). Наприклад, якщо фермер посіяв культуру A2, а літо було дощовим, то прибуток фермера дорівнює a2h22.
Приклад 2.8. (Вибір асортименту товарів). На базі торгової організації є n типів одного з товарів асортиментного мінімуму. У магазин повинен бути завезений тільки один з типів даного товару. Потрібно вибрати той тип товару, що доцільно завезти в магазин. Якщо товар типу j буде користатися попитом, то магазин від його реалізації дістане прибуток pj, якщо ж він не буде користатися попитом – то збиток qj. Скласти математичну модель цієї задачі в умовах невизначеного попиту. Керуючись формалізацією задачі прикладу 1.7, обґрунтуйте, що шукана модель має вигляд:

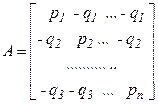.                                     (2.14)

Поясніть задачу магазину на цій моделі.
Приклад 2.9. (Планування оптимального терміну закінчення робіт). Компанія повинна реалізувати проект будівництва об'єкта, що складається з n операцій (робіт). Керівники комплексу оцінили тривалість виконання кожної операції та установили послідовність операцій, тобто точно визначили, які операції обов'язково повинні бути закінчені, щоб могла початися кожна з операцій, що входить у комплекс. Керівництву компанії треба з'ясувати, яка найменша можлива тривалість реалізації всього проекту, тобто найбільш ранній із усіх можливих термінів його завершення.
Під час побудови математичної моделі припустимо, що проект складається з п'яти операцій А, В, С, Д, Е. За умовою відома послідовність операцій і їх тривалість. Нехай ці дані будуть такими, як показано в табл.2.1:

Таблиця 2.1 – Послідовність та тривалість операцій

Операції

Безпосередньо попередні операції

Тривалість операцій

А

-

T

В

-

T

С

А

T

D

А

T

Е

B,D

tE

F

С,Е

-

Фіктивна операція F, що починається в момент завершення проекту, вводиться для зручності (див. нижче). Другий стовпець таблиці означає, що операцію С не можна почати перш ніж незакінчена операція А і т. д.
Приймемо, що змінними є терміни початку операції (введемо лише ті з них, що потрібні для вирішення задачі):
yCD - момент початку операцій С і D;
yЕ - момент початку операції Е;
yF - момент початку операції F.
Тут, yF – момент завершення всього комплексу. Моменти yА і yВ –моменти початку операцій, оскільки операції А і В не мають попередніх. При цьому математична модель має вигляд:
min yF                                            (2.15)
за обмежень: yCD ≥ tA;   yE ≥ tB;   yE ≥ tD + yCD;   yF ≥ tC + yCD;   yF ≥ tE + yE .

2.4 Класифікація математичних моделей системного аналізу

Класи задач математичних моделей системного аналізу (дослідження операцій) можна класифікувати, виходячи з елементів загальної структури (2.1), розглядаючи їх характеристики з різних точок зору. Тому одне тільки перерахування назв зайняло б кілька сторінок. Тут ми визначимо тільки найбільші класи математичних моделей задач. Почнемо з характеристики середовища S моделей прийняття рішень.
Якщо елементи математичної моделі (2.1) не залежать від часу, тобто процес прийняття рішення зводиться до миттєвого акту вибору точки із заданої множини, то математична модель системного аналізу називається статичною. Інакше, тобто коли прийняття рішення є багатоетапним (дискретним) або неперервним у часі процесом, то така модель називається динамічною. Приклади 2.1-2.4, 2.7 і 2.8 попереднього розділу відносяться до статичних, а приклади 2.5, 2.6 і 2.9 – до динамічних моделей. Моделі, що не містять випадкових величин і ймовірнісних явищ називаються детермінованими (приклади 2.1, 2.2, 2.4, 2.5, 2.9), а якщо моделі характеризуються випадковими вели­чинами з ймовірнісними оцінками, то вони називаються стохастичними (при­клади 2.3, 2.4, 2.6).
Залежно від кількості ОПР розрізняють моделі прийняття оптимальних рішень і математичні моделі в умовах протидії (ігрові моделі (n ≥ 2, де n - число елементів на множині N)). Ігрова модель (або гра) – це математична модель задачі прийняття рішення в умовах конфлікту, тобто в тих ситуаціях, коли має місце протистояння інтересів двох або більше сторін. У загальному випадку, залежно від характеру конфлікту, розрізняють антагоністичні (приклади 2.7, 1.8), неантагоністичні (безкоаліційні) і кооперативні ігри.
Якщо в моделях всі елементи лінійні (цільова функція та обмеження), то отримуємо моделі лінійного програмування (приклади 2.1 і 2.2), інакше – отримуємо моделі нелінійного програмування (приклади 2.3 і 2.4,якщо функції Rj і Kj – нелінійні). Якщо ж у моделях присутній фактор часу, то такі моделі називаються моделями оптимального керування (приклад 2.5). Іноді такі моделі називають моделями динамічного програмування. Однак це не точна назва, оскільки динамічне програмування – це назва методу розв’язання задач оптимального керування.
У реальних випадках часто в ОПР переслідує не одну, а кілька цілей. Математичні моделі <X; f1,…,fn; Σ >, що відповідають цьому, називаються моделями багатокритеріальної (векторної) оптимізації. Так, наприклад, у моделі (2.5) ОПР вибирає рішення х Î Х таким чином, щоб отримати як можна більші значення f1(x),...,fn(x) критеріїв.
Є також і такі класи математичних моделей, що отримали свою назву, виходячи з їх призначення: системи масового обслуговування (приклад 2.6), задачі керування запасами (приклад 2.3), задачі мережевого і календарного планування (приклад 2.9).
Для повноти сприйняття нижче наведемо ті «класичні» моделі задач системного аналізу, що, завдяки їх типовості, зустрічаються у багатьох підручниках з математичного програмування. Деякі з них відносяться до початку виникнення теорії оптимізації і теорії систем. Деякі з наведених нижче прикладів служать для ілюстрації деяких видів моделей прийняття рішень і не претендують на реальність, це «навчальні моделі». Моделі, що становлять безпосередній практичний інтерес, будуть докладнішими, глибшими і складнішими. Навчальні ж задачі – це перше наближення до реальних (практичних) задач, їх спрощений аналог. Керуючись матеріалами попередніх двох підрозділів, можливо самостійно отримати їх математичні моделі.
Задача оптимального розкрою матеріалу. Фірма виготовляє виріб, що складається з р деталей (наприклад, комплект постільної білизни). Причому в один виріб ці деталі входять у кількостях k1,…,kp. З цією метою визначається розкрій m партій матеріалу. У i-ій партії є bi одиниць матеріалу. Кожну одиницю матеріалу можна розкроїти на деталі n способами. Під час розкрою одиниці i-ої партії j-им способом виходить аijp деталей p-го виду. Потрібно скласти такий план розкрою матеріалів, щоб з них отримати максимальне число виробів.
Транспортна задача. Є n постачальників і m споживачів деякого однорідного продукту. Відомі випуск продукції в кожного постачальника і потреби в ній кожного споживача, а також витрати на перевезення продукції від постачальників до споживачів. Треба побудувати план транспортних перевезень з мінімальними транспортними витратами з урахуванням пропозицій постачальників і попиту споживачів.
Задача про призначення на роботу. Є n робіт і m виконавців. Вартість виконання роботи i виконавцем j дорівнює cij. Потрібно розподілити виконавців на роботи так, щоб мінімізувати витрати.
Задача про суміші (про раціон). З m видів вихідних матеріалів, кожний з який складається з n компонентів, скласти суміш, у якій зміст компонентів повинен бути не менше b1,...,bn. Відомі ціни одиниці матеріалів: c1...cm і питома вага j-гo компонента в одиниці i-гo матеріалу. Треба скласти суміш, у якій витрати були б мінімальними.
Задача про рюкзак. Є n предметів. Вага предмета i дорівнює pi, а його цінність – cі (i = l,…,n). Потрібно для заданої цінності вантажу вибрати сукупність предметів мінімальної ваги.
Задача про комівояжера. Є n деяких міст і задана відстань cij між ними (i, j = l....,n). Виїжджаючи з одного (вихідного) міста, комівояжер повинен побувати  в усіх інших містах по одному разу і повернутися у вихідне місто. Треба визначити, у якому порядку слід об'їжджати міста, щоб сумарна пройдена відстань була найменшою.
Задача про верстати. На універсальному верстаті обробляються однакові партії з n деталей. Перехід від оброблення деталі i до оброблення деталі j вимагає переналагодження верстата, що займає cij часу. Потрібно визначити послідовність оброблення деталей, за якою загальний час пере­налагоджень верстата при обробленні партії деталей був би мінімальним.
Задача про розподіл капіталовкладень. Є n проектів, причому для кожного проекту i відомий очікуваний ефект γi від його реалізації і необхідна величина капіталовкладень gi. Загальний обсяг капіталовкладень не може перевищувати заданої величини b. Потрібно визначити, які проекти необхідно реалізувати, щоб сумарний ефект був найбільшим.
Задача про розміщення виробництва. Планується випуск m видів продукції, що могли б вироблятися на n підприємствах (n > m). Витрати виробництва і збуту одиниці продукції, плановий обсяг річного виробництва продукції і планова вартість одиниці продукції кожного виду відомі. Потрібно з n підприємств вибрати такі m підприємств, кожне з яких буде виробляти один вид продукції.

2.5 Моделювання систем в умовах визначеності

Класичним прикладом найпростішої задачі системного аналізу в умо­вах визначеності може бути задача виробництва і постачання товару. Нехай деяка фірма повинна виробляти і поставляти продукцію клієнтам рівномірними партіями у кількості N = 24000 одиниць за рік. Зрив постачань неприпустимий, оскільки штраф за це можна вважати нескінченно великим. Запускати у виробництво слід відразу всю партію (такі умови технології). Вартість збереження одиниці продукції Cx = 10 копійок на місяць, а вартість запуску однієї партії у виробництво (незалежно від її обсягу) складає Cp = 400 грн. Таким чином, запускати в рік багато партій явно невигідно, але й невигідно і випустити всього 2 партії в рік – занадто великі витрати на збереження! Скільки ж партій на рік найкраще буде випускати?
Побудуємо математичну модель такої системи. Позначимо через n розмір партії і знайдемо кількість партій за рік – p = N/n = 24000/n. Виходить, що інтервал часу між партіями складає t = 12/p (місяців), а середній запас виробів на складі – n/2 штук. Скільки ж нам буде коштувати випуск партії в n штук за один раз?
Підрахувати неважко – 0,1×12×n/2 гривень на складські витрати у рік і 400×p гривень за запуск партій з n штук виробів у кожній.
У загальному вигляді річні витрати складають
E = T n / 2 + N / n,                                    (2.16)
де T=12 – повний час спостереження у місяцях.
Таким чином, перед нами постає типова варіаційна задача: знайти таке n0, за яким сума E досягає мінімуму.
Розв’язок цієї задачі знайти зовсім просто – треба взяти похідну за n і прирівняти цю похідну до нуля. Це дає
n0=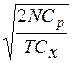,                                                  (2.17)
що для нашого прикладу складає 4000 одиниць в одній партії і відповідає інтервалу випуску партій величиною у 2 місяці. Витрати при цьому мінімальні і визначаються як
E0 =,                                             (2.18)
що для нашого прикладу складає 4800 гривень в рік.
Зіставимо цю суму з витратами за умови випуску 2000 виробів у партії або випуску партії один раз на місяць:
E1 =0.1×12×2000/2 + 400×24000/ 2000 = 6000 гривень у рік.
Коментарі, як кажуть, – зайві!
Зазвичай, так просто розв’язувати задачі прийняття оптимальних стратегій вдається далеко не завжди, навіть якщо мова йде про детерміновані дані щодо опису життя системи – її моделі. Існує цілий клас задач системного аналізу і відповідних їм моделей систем, де мова йде про необхідність мінімізувати одну функцію багатьох змінних такого типу:
E=a1X1+a2X2+...+anXn,                                           (2.19)
де Xi – шукані змінні;
ai  – відповідні їм коефіцієнти або “ваги змінних” і при цьому мають місце обмеження як на змінні, так і на їх ваги.
Такі задачі добре досліджені у спеціальному розділі прикладної математики – лінійному програмуванні. Ще в докомп’ютерні часи були роз­роблені алгоритми пошуку екстремумів функцій E=f (a, X), які назвали – цільовими. Вони використовуються і зараз, і є основою для розроблення прикладних програм системного аналізу. При цьому системний підхід до розв’язання практичних задач керування, зокрема для задач з багатьма змінними призвів до появи спеціалізованих типових напрямків як у області теорії аналізу, так і у практиці. “Найстаршими” і, отже, найперевіренішими є методи, що давно вже називають класични­ми. Фахівцям у галузі ділового адміністрування треба знати ці задачі хоча б на рівні постановки (див. підрозділ 2.1) і, головне, у плані моделювання відповідних систем.
Початки теоретичного обґрунтування і розроблення практичних методів розв’язання задач лінійного програмування були покладені Д. Данцигом (за іншою версією – Л. В. Канторовичем). Для більшості конкретних додатків універсальним вважається так званий симплекс-метод пошуку мети. Для нього і супутніх йому методів розроблено багато спеціальних пакетів прикладних програм (ППП).

2.6 Наявність декількох цілей – багатокритеріальні системи

Часто етап змістовної постановки задачі системного аналізу приводить нас до висновку про наявність кількох цілей функціонування системи. І справді, якщо деяка, наприклад, економічна система може мати “головну мету” – досягнення максимального прибутку, то майже завжди можна спостерігати ситуацію наявності обмежень або умов. Порушення цих умов або неможливе (тоді не буде самої системи), або свідомо призводить до неприпустимих наслідків для зовнішнього середовища. Коротше кажучи, ситуація, коли мета всього одна і досягти її потрібно за будь-яку ціну, практично неможлива.
Так, наприклад, нехай є найпростіша ситуація багатокритеріальності – існують тільки дві мети системи T1 і T2 і тільки дві можливих стратегії S1 і S2.
Нехай ми оцінили ефективність E11 стратегії S1 щодо T1, і ефективність цієї стратегії виявилася рівною 0,4 (за деякою шкалою 0...1). Здійснивши таке ж оцінювання для всіх стратегій і всіх цілей, ми отримали таблицю 2.2 (матрицю ефективностей):

Таблиця 2.2 – Матриця ефективностей

E

T1

T2

S1

0,4

0,6

S2

0,7

0,3

Яку ж із стратегій вважати найкращою? Поки ми не обговоримо значимість кожної з цілей і не вкажемо їх ваги – сперечатися марно! От якби нам було відомо, що перша ціль, наприклад, у 3 рази  важливіша другої, то тоді можна врахувати їх відносні ваги – скажімо величинами 0,75 для першої і 0,25 для другої. За таких умов сумарні ефективності стратегій (щодо усіх цілей) складуть:
для першої E1 = 0,4×0,70+0,6×0,30=0,28+0,18=0,46;
для другої E2= 0,8×0,70+ 0,2×0,25=0,56+0,05=0,61.
Так що відповідь на запитання про вибір стратегії далеко не очевидна. Отже, критерій ефективності системи за наявності декількох цілей доводиться описувати через ефективності окремих стратегій виду

Es=S StUt ,

тобто враховувати ваги окремих цілей Ut.
Якщо ви уважно стежили за міркуваннями під час розгляду прикладу (2.16), то зможете зрозуміти, що насправді там мова йшла про дві цілі. З одного боку, ми хотіли б мати якомога менші партії – їх дешевше зберігати (малий термін зберігання). З іншого боку, нам були б бажані великі партії, оскільки при цьому менші витрати на запуск партій у виробництво. Якби ми перебирали усі 365 можливих стратегій (від зміни партії щодня до однієї в рік), то, звичайно ж, знайшли б оптимальну стратегію зі зміною партій кожні два місяці. Інша справа, що в нашому розпорядженні була аналітична модель системи (формула сумарних витрат).
Отож – вагові коефіцієнти цілей у тій моделі були рівними і ми їх могли не помічати під час пошуку мінімуму витрат. Ну, а що робити, якщо “важливість” цілей доводиться вимірювати не по шкалі Int або Rel, тобто в числовому вигляді, а по шкалі Ord? Іншими словами – звідки беруться вагові коефіцієнти цілей?
Не часто вагові коефіцієнти визначаються однозначно за “фізичним змістом” задачі системного аналізу. Частіше усього їх відшукування можна називати “призначенням”, “придумуванням”, “пророкуванням” – тобто ніяк не «науковими» діями. Іноді, як не дивно це звучить, вагові коефіцієнти призначаються шляхом голосування – явного або таємного. Справа у тому, що у ситуаціях, коли немає числового методу оцінювання ваги цілі, реальним виходом з положення є використання накопиченого досвіду.
Нерідко вагові коефіцієнти задає безпосередньо ОПР, але частіше її досвід керування підказує: одна голова – добре, а багато розумних голів – набагато краще. Приймається особливе рішення – використання методу експертних оцінок. Суть цього методу досить проста. Потрібно чітко обговорити всі цілі функціонування системи і запропонувати групі осіб, високо компетентних у даній галузі (експертів), хоча б розташувати всі цілі за значимістю за «призовими місцями», або, мовою ТССА, за рангами.
Вищий ранг (зазвичай 1) означає найбільшу важливість (вагу) цілі, наступний за ним – трохи меншу вагу і т. д. Спеціальний розділ непараметричної статистики – теорія рангової кореляції, дозволяє перевірити гіпотези про значимість отриманої від експертів інформації. Розвиток рангової коре­ляції, її інший розділ, дозволяє встановлювати згоду, тобто узгодженість думок експертів або рангову конкордацію. Це особливо важливо у випадках, коли не тільки виникла потреба використовувати думки експертів, але й існує сумнів у їх компетентності.

2.7 Експертні оцінки, рангова кореляція і конкордація

Нехай у процесі системного аналізу нам довелося враховувати деяку величину U, вимірювання якої можливе лише за порядковою шкалою (Ord). Наприклад, нам доводиться враховувати 10 цілей функціонування системи і потрібно з'ясувати їх відносну значимість, тобто питому вагу.
Якщо існує група осіб, компетентність яких у даній області не викликає сумнівів, то можна опитати кожного з експертів,запропонувавши їм розташувати цілі за важливістю або «проранжувати» їх. У найпростішому випадку можна не дозволяти повторювати ранги, хоча це необов'язково – повторення рангів завжди можна врахувати. Результати експертного оцінювання в нашому прикладі опишемо в табл. 2.3 рангів цілей.
Отже, для кожної з цілей Ti ми можемо знайти суму рангів, що визначені експертами, а потім сумарний або результуючий ранг мети Ri. Якщо суми рангів збігаються – призначається середнє значення.

Таблиця 2.3 – Результати експертного оцінювання

Експерти

1

2

3

4

5

6

7

8

9

10

Сума

A

3

5

1

8

7

10

9

2

4

6

55

B

5

1

2

6

8

9

10

3

4

7

55

Сума рангів

8

6

3

14

15

19

19

5

8

13

 

Сумарний ранг

 4,5

   3

   1

   7

   8

 9,5

 9,5

   2

 4,5

   6

55

Метод рангової кореляції дозволяє відповісти на запитання – наскільки корельовані невипадкові ранжировки кожного з двох експертів, а значить – наскільки можна довіряти результуючим рангам?
Зазвичай, висувається основна гіпотеза – про відсутність зв'язку між ранжировками і встановлюється ймовірність справедливості цієї гіпотези. Для цього можна використовувати два підходи: визначення коефіцієнтів рангової кореляції Спірмена або Кенделла.
Простішим у реалізації є перший метод, за яким обчислюється значення коефіцієнта Спірмена.
Rs=1-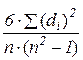,                                           (2.21)
де di визначаються різницями рангів першої і другої ранжировок по n об'єктів у кожній.
У нашому прикладі сума квадратів різниць рангів складає 30, а коефіцієнт кореляції Спірмена близько 0,8, що дає значення ймовірності гіпотези про повну незалежність двох ранжировок усього лише 0,004.
При необхідності можна скористатися послугами групи з m експертів, встановити результуючі ранги цілей, але тоді виникне питання про узгодженість думок цих експертів або конкордації.
Нехай у нас є ранжировки 4 експертів стосовно 6 факторів, що визначають ефективність деякої системи (див. у табл. 2.4).
Відзначимо, що повна сума рангів складає 84, що дає  у середньому по 14 на фактор. Для загального випадку n факторів і m експертів середнє значення суми рангів для будь-якого фактора визначиться виразом
D.                                       (2.22)
Тепер можна оцінити ступінь узгодженості думок експертів щодо шести факторів. Для кожного з факторів спостерігається відхилення суми рангів, зазначених експертами, від середнього значення такої суми, як це показано в табл. 2.4.

Таблиця 2.4 - Відхилення суми рангів, зазначених експертами

Фактори >
Експерти

1

2

3

4

5

6

Сума

A

5

4

1

6

3

2

21

B

2

3

1

5

6

4

21

C

4

1

6

3

2

5

21

D

4

3

2

3

2

5

21

Сума рангів
cум. ранг

15
4

11
2

10
1

19
6

12
3

17
5

84

Відхилення суми
від середнього

+1
1

-3
9

-4
16

+5
25

-2
4

+3
9

0
64

Оскільки сума цих відхилень завжди дорівнює нулю, для їх усереднення розумним буде використовувати квадрати значень.
У нашому випадку сума таких квадратів складе S = 64, а в загальному випадку ця сума буде найбільшою тільки при повному збігу думок всіх експертів стосовно всіх факторів:
Smax =.                                      (2.23)
М. Кенделлом запропоновано показник узгодженості або коефіцієнт конкордації (concordationrate), що визначається як
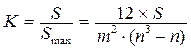.                                    (2.24)
У нашому прикладі значення коефіцієнта конкордації складає близько 0,229, що для чотирьох експертів і шести факторах достатньо, щоб з ймовірістю не більше 0,05 вважати думки експертів неузгодженими. Справа у тому, що саме випадковість ранжировок, їх некорельованість прораховується досить просто. Так, для нашого прикладу, зазначена ймовірність відповідає сумі квадратів відхилень S = 142,3, що набагато більше 64.
На закінчення відзначимо ще дві таких обставини про особливості методу експертних оцінок у системному аналізі.
У першому прикладі ми одержали результуючі ранги 10 цілей функціонування системи. Як скористатися цим і як перейти від рангової (Ord) шкали цілей до шкали вагових коефіцієнтів, тобто у діапазоні від 0 до 1? Тут, звичайно, використовуються елементарні прийоми нормування. Якщо ціль 3 має ранг 1, ціль 8 має ранг2 і т. д., а сума рангів складає 55, то ваговий коефіцієнт для мети 3 буде най­більшим і сума ваг усіх десяти цілей складе 1.
Вагу цілі доведеться визначати як:
(11-1)/55 для  цілі 3;
(11-2)/55 для  цілі 8 і т. д.
Під час використання групової експертної оцінки можна не тільки з'ясовувати думку експертів щодо показників, необхідних для системного аналізу. Дуже часто в подібних ситуаціях використовують так званий метод Дельфі (від легенди про дельфійського оракула). За ним опитування експертів проводять у кілька етапів, як правило – анонімно. Після чергового етапу від експерта потрібна не просто ранжировка, але й її обґрунтування. Ці обґрунтування повідомляються усім експертам перед черговим етапом без вказування авторів обґрунтувань. Наявний досвід свідчить про можливість істотно підвищити показовість, обґрунтованість і, головне, вірогідність суджень експертів. Як «побічний ефект» можна скласти думку про професійність кожного експерта.

Запитання і завдання для самоконтролю

  • В чому полягає мета ОПР?
  • З яких загальних принципів (етапів) складається дослідження задач системного аналізу?
  • В чому мета математичного моделювання?
  • Назвіть основні елементи математичної моделі будь-якої задачі системного аналізу з прийняттям рішень.
  • Шо таке критерій якості  ОПР?
  • Якою є загальна структура задачі прийняття рішення з багатьма учасниками?
  • Назвіть основні етапи математичного моделювання.
  • Охарактеризуйте задачу планування добового випуску продукції.
  • Охарактеризуйте задачу розміщення замовлень.
  • Охарактеризуйте задачу вибору портфеля цінних паперів.
  • Охарактеризуйте задачу про рекламу.
  • Охарактеризуйте задачу керування виробництвом.
  • Охарактеризуйте задачу оптимізації схеми обслуговування.
  • Охарактеризуйте задачу вибору оптимального виду посівної культури.
  • Охарактеризуйте задачу вибору асортименту товарів.
  • Охарактеризуйте задачу планування оптимального терміну закінчення робіт.
  • Опишіть класифікацію математичних моделей системного аналізу
  • Охарактеризуйте моделювання систем в умовах визначеності на прикладі задачі виробництва та постачання товару.
  • Що таке коефіцієнт конкордації?
  • Як працює метод експертних оцінок? Поясніть на прикладі.