3.МОДЕЛЮВАННЯ СИСТЕМ В УМОВАХ НЕВИЗНАЧЕНОСТІ

Як уже відзначалося, у більшості реальних великих систем не обійтися без врахування “станів природи” – впливів стохастичного типу, випадкових величин або випадкових подій. Це можуть бути не тільки зовнішні впливи на систему в цілому або на окремі її елементи. Дуже часто і внутрішні системні зв'язки мають таку ж, “випадкову” природу. Важливо зрозуміти, що стохастичність зв'язків між елементами системи є основним чинником ризику виконати замість системного аналізу зовсім безглузду роботу, тобто отримати як рекомендації з керування системою заздалегідь неприйнятні  рішення.
Вище вже було прийнято, що у таких випадках замість самої випадкової величини X доводиться використовувати її математичне сподівання Mx. Усе  начебто б просто – не знаємо, так очікуємо. Але наскільки виправдані наші сподівання? Яка впевненість або яка ймовірність помилитися? Такі запитання вирішуються, відповіді на них отримати можна – але для цього треба мати інформацію про закон розподілу ВВ. От і доводиться на даному етапі системного аналізу (етапі моделювання) займатися статистичними дослідженнями, тобто намагатися отримати відповіді на запитання:
- чи є даний елемент системи і вироблені ним операції “класичними”?
- чи немає підстав використовувати теорію для визначення типу розподілу ВВ(продукції, грошей або інформаційних повідомлень)? А якщо це так, то можна сподіватися на оцінки помилок під час прийняття рішень. Якщо ж це не так, то доводиться ставити питання інакше:
- чи не можна отримати шуканий розподіл ВВ із даних експерименту?
Якщо цей експеримент обійдеться дорого або фізично чи морально неможливий, то скористатися апостеріорними даними, досвідом минулого або пророкуваннями на майбутнє, експертними оцінками? Якщо ж і тут немає підстав для прийняття позитивних рішень, то можна сподіватися ще на один вихід з положення. Не завжди, але усе-таки можливо використовувати поточний стан вже діючої системи, її реальне “життя” для отримання глобальних показників функціонування системи. Для цієї мети слугують методи планування експерименту, теоретичною і методологічною основою яких є особлива область системного аналізу – так званий факторний аналіз, сутність якого буде пояснена нижче.

3.1 Основні поняття математичної статистики

3.1.1 Випадкові події і величини та їх основні характеристики

Як уже говорилося, під час аналізу великих систем наповнювачем каналів зв'язку між елементами, підсистемами і системи в цілому може бути:
- продукція, тобто реальні, фізично відчутні предмети із заздалегідь заданим способом їх кількісного і якісного опису;
- гроші, з єдиним способом опису – сумою;
- інформація, у вигляді повідомлень про події в системі і значеннях величин, що описують її поведінку.
Почнемо з того, що звернемо увагу на тісний (системний) зв'язок показників продукції і грошей з інформацією про ці показники. Якщо розглядати деяку фізичну величину, скажімо – кількість проданих за день зразків продукції, то відомості про цю величину після продажу можуть бути отримані без проблем і досить точно або достовірно. Однак, зрозуміло, що під час аналізу нас куди більше цікавить майбутнє – а скільки цієї продукції буде продано за день? Це запитання дуже важливе, оскільки нашою метою є керування, а образно висловлюючись, “керувати – значить передбачати”.
Отже, без попередньої інформації, тобто знань про кількісні показники в системі нам не обійтися. Величини, що можуть приймати різні значення залежно від зовнішніх щодо них умов, прийнято називати випадковими (randomsize) (стохастичними за природою). Так, наприклад, стать зустрінутої нами людини може бути жіночою або чоловічою (дискретна випадкова величина), причому її зріст також може бути різним, але це вже неперервна випадкова величина з тією або іншою кількістю можливих значень (залежно від одиниці вимірювання).
Для випадкових величин (далі – ВВ) доводиться застосовувати статистичні методи їх опису. Залежно від типу самої ВВ – (дискретна або неперервна) це робиться по-різному.
Дискретний опис полягає у тому, що вказуються всі можливі значення даної величини (наприклад, 7 кольорів звичайного спектра) і для кожної з них вказується  ймовірність або частота спостережень саме цього значення для нескінченно великої кількості всіх спостережень. Можна довести (і це давно зроблено), що при збільшенні числа спостережень в певних умовах за значеннями деякої дискретної величини частота повторень даного значення буде усе більше наближатися до деякого фіксованого значення, яке і буде ймовірністю цього значення.
До поняття ймовірності значення дискретної ВВ можна підійти й іншим шляхом – через випадкові події. Це найпростіше поняття з теорії ймовірностей і математичної статистики – подія з ймовірністю «0,5» або 50% у 50 випадках зі 100 може відбутися або не відбутися, якщо ж її ймовірність більша «0,5» – вона частіше відбувається, аніж не відбувається. Події з ймовірністю «1» називають вірогідними, а з ймовірністю «0» – неможливими. Звідси просте правило: для випадкової події X сума ймовірностей P(X) (подія відбувається) і P() (подія не відбувається) для простої події дає «1».
Якщо ми спостерігаємо за деякою складною подією, наприклад, випаданням чисел 1...6 на верхній грані гральної кості, то можна вважати, що така подія має множину варіантів і для кожного з них ймовірність складає 1/6 за умови симетричності кості. Якщо ж кость несиметрична, то ймовірності окремих чисел будуть різними, однак їх сума буде дорівнювати 1. Однак якщо розглядати результат кидання кості як дискретну випадкову величину, то прийдемо до поняття розподілу ймовірностей такої величини.
Нехай у результаті досить великого числа спостережень за гранню однієї і тієї ж кості ми отримали такі дані:

Таблиця 3.1 – Таблиця спостережень за випадковими величинами

Грані

1

2

3

4

5

6

Разом

Спостереження

140

80

200

400

100

80

1000

Подібну таблицю спостережень за ВВ часто називають вибірковим розподілом, а відповідну їй діаграму – гістограмою (рис.3.1).


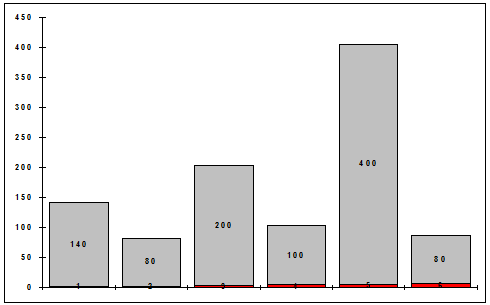
Рисунок 3.1 – Гістограма

Яку ж інформацію несе така таблиця або відповідна їй гістограма?
Насамперед, всю – оскільки іноді і таких даних про значення випадкової величини немає і їх доводиться або отримувати (експеримент, моделювання), або вважати результати такої складної події рівноможливими – по для кожного з варіантів.
З іншого боку, інформації дуже мало, особливо в цифровому, чисельному описі лише самої ВВ. Як, наприклад, відповісти на запитання: – а скільки в середньому ми виграємо за одне кидання кості, якщо виграш відповідає числу, що випало на грані? Неважко підрахувати:
1´0,140+2´0,080+3´0,200+4´0,400+5´0,100+6´0,080 = 3,48
Те, що ми обчислили, називається середнім значенням випадкової величини, якщо нас цікавить минуле. Якщо ж ми поставимо запитання інакше, тобто оцінити за цими даними наш майбутній виграш, то відповідь 3,48 прийнято називати математичним сподіванням випадкової величини, що у загальному випадку визначається як
Mx = å Xi×P(Xi),                                            (3.1)
де P(Xi) – ймовірність того, що X прийме своє i-е чергове значення.
Таким чином, математичне сподівання випадкової величини (як дискретної, так і неперервної) – це те, до чого прямує її середнє значення для досить великої кількості спостережень. Звертаючись до нашого прикладу, можна помітити, що кость несиметрична, інакше ймовірності складали б по 1/6 кожна, а середнє і математичне сподівання склало б 3,5. Тому доречне таке запитання – а яка ступінь асиметрії кості, і – як її оцінити за підсумками спостережень? Для цієї мети використовується спеціальна величина – міра розсіювання – так само як ми «усереднювали» допустимі значення ВВ, можна усереднити її відхилення від середнього. Але оскільки різниці (Xi-Mx) завжди будуть компенсувати одна одну, то доводиться усереднювати не відхилення від середнього, а квадрати цих відхилень. Величину прийнято називати дисперсією  випадкової величини X: =, яку можна простіше обчислити, якщо скористатися виразом
.                       (3.2)
Виконаємо таке обчислення для ВВ з розподілом на рис. 3.1. Дані для обчислень занесено в табл. 3.2.

Таблиця 3.2 - Дані для обчислень ВВ

Грані (X)

1

2

3

4

5

6

Разом

X2

1

4

9

16

25

36

 

Pi

0,140

0,080

0,200

0,400

0,100

0,080

1,00

Pi Х 2 1000

140

320

1800

6400

2500

2880

14040

Таким чином, дисперсія складе 14,04 - (3,48)2 = 1,930.
Зазначимо, що величина дисперсії не збігається з величиною самої ВВ і це не дозволяє оцінити величину розкиду. Тому найчастіше замість дисперсії використовується квадратний корінь з її значення – середньо-квадратичне відхилення або відхилення від середнього значення:
,                                               (3.3)
складає в нашому випадку . Багато це чи мало?
Відзначимо, що у випадку спостереження тільки одного з можливих значень (розкиду немає) середнє дорівнювало б саме цьому значенню, а дисперсія склала б 0. І навпаки – якби всі значення спостерігалися однаково часто (були б рівноможливими), то середнє значення склало б
 
середній квадрат відхилення визначиться як

а дисперсія – як 15,167 - 12,25 = 3,917.
Таким чином, найбільшерозсіювання значень ВВ має місце при її рівноможливому або рівномірному розподілі.
Слід відзначити, що значення і є розмірними і їх абсолютні значеннями мало про що говорять. Тому, часто для грубого оцінювання «випадковості» даної ВВ використовують коефіцієнт варіації або відношення кореня квадратного з дисперсії до величини математичного сподівання
=,                                            (3.4)
у нашому прикладі ця величина складе 1,389/3,48 = 0,399.
Отже, запам'ятаємо, що невипадкова, тобто детермінована величина має математичне сподівання, що дорівнює їй самій, нульову дисперсіюта нульовий коефіцієнт варіації, у той час, як рівномірно розподілена ВВ має максимальну дисперсію і максимальний коефіцієнт варіації.
У багатьох ситуаціях доводиться мати справу з неперервно-розподіленими ВВ – вагами, відстанями і под. Для таких величин ідея оцінювання середнього значення (математичного сподівання) і міри розсіювання (дисперсії) залишається тією ж, що і для дискретних ВВ. Доводиться тільки замість відповідних сум обчислювати інтеграли.
Другою відмінністю для неперервних ВВ є те, що питання про те, яка ймовірність прийняття нею конкретного значення, зазвичай не має сенсу, тобто, як перевірити, що вага товару складає точно 242 кг – і не більше і не менше (визначити точно неможливо)?
Для усіх ВВ – як дискретних, так і неперервно розподілених, має велике значення питання про діапазон їх значень. І справді, іноді знання ймовірності події, що випадкова величина не перевищить задану границю, є єдиним  способом використовувати наявну інформацію для системного аналізу і системного підходу щодо задачі керування системою. При цьому правило визначення ймовірності влучення у необхідний діапазон, дуже просте – потрібно додати ймовірності окремих дискретних значень діапазону або проінтегрувати криву розподілу на цьому діапазоні.

3.1.2 Взаємозв'язки випадкових подій

Звернемося знову до поняття випадкових подій і розглянемо спочатку прості події (може відбутися або ні). Ймовірність події Х позначимо через Р(Х) і розумітимемо, що ймовірність того, що подія не відбудеться, складає
.                                             (3.5)
Найважливішим під час розгляду декількох випадкових подій (тим більше в складних системах з розвиненими зв'язками між елементами і підсистемами) – є розуміння способу визначення ймовірності одночасного настання декількох подій або – сумісності подій.
Розглянемо найпростіший приклад двох подій X і Y, ймовірності яких складають P(X) і P(Y). Тут важливе лише одне питання – ці події не­залежні або навпаки взаємозалежні, що приводить до ще одного запитання – яка міра зв'язку між ними? Спробуємо розібратися в цьому питанні.
Оцінимо спочатку ймовірність одночасного настання двох незалежних подій. Елементарні міркування приведуть нас до висновку: якщо події незалежні, то при 80%-й ймовірності X і 20%-й ймовірності Y одночасне їх настання має ймовірність усього лише =0,16, тобто 16%. Отже, ймовірність настання двох незалежних подій визначається добутком їх ймовірностей:
.                                     (3.6)
Перейдемо тепер до залежних подій. Назвемо ймовірність події X за умови, що подія Y уже відбулася, умовною ймовірністю P(X/Y), вважаючи при цьому P(X) безумовною або повною ймовірністю. Такі ж прості міркування приводять до так званої  формули Байєса
,                           (3.7)
де у лівій і правій частині записані ймовірності одночасного настання двох «залежних» або корельованих подій.
Доповнимо цю формулу загальним виразом, що описує безумовну ймовірність події X:
,                (3.8)
яка означає, що подія X може відбутися або після того як подія Y відбулася, або після того, як вона не відбулася () – третього не може бути!
Формули Байєса (байєсівський підхід) до оцінювання ймовірнісних зв'язків для простих подій і дискретно розподілених ВВ відіграють вирішальну роль у теорії прийняття рішень в умовах невизначеності, наслідків цих рішень або в умовах протидії з боку природи, або інших великих систем (конкуренції). За цих умов ключовою буде стратегія керування, що заснована на прогнозі апостеріорної (післядослідної) ймовірності події
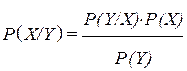.                                        (3.9)
Насамперед, ще раз відзначимо взаємний зв'язок подій X і Y, і якщо одна не залежить від іншої, то вищенаведений вираз перетвориться на тривіальну тотожність. До речі, ця обставина використовується під час розв’язання задач оцінювання тісноти зв'язків, тобто під час кореляційного аналізу. Якщо ж взаємозв'язок подій має місце, то формула Байєса дозволяє вести керування шляхом оцінювання ймовірності досягнення деякої мети на основі спостережень над процесом функціонування системи, тобто, шляхом перерахунку варіантів стратегій з урахуванням уявлень, що змінились, тобто нових значень ймовірностей. Справа у тому, що будь-яка стратегія керування буде будуватися на базі певних уявлень про ймовірність подій у системі і на перших кроках ці ймовірності будуть узяті «з голови» або у кращому випадку з досвіду керування іншими системами. Однак впродовж «життя» системи не можна відкидати можливість керування, тобто використання всього здобутого дотепер досвіду.

3.1.3 Схеми і закони розподілу випадкових подій та величин

Значну роль у теорії і практиці системного аналізу відіграють стандартні розподіли неперервних і дискретних ВВ. Ці розподіли іноді називають «теоретичними», оскільки для них розроблено формальні методи розрахунку усіх показників, зафіксовані зв'язки між ними та побудовані алгоритми їх розрахунку і под. Таких класичних законів розподілу досить багато, хоча їх «штат» за останні 30..50 років практично не поповнився. Необхідність знайомства з ними пояснюється тим, що вони відповідають «теоретичним» схемам випадкових (здебільшого елементарних) подій.
Як уже відзначалося, наявність великих масивів взаємозалежних подій і велика кількість випадкових величин, наприклад, у системах економіки призводить до труднощів апріорного оцінювання законів розподілів цих подій або величин. Нехай, наприклад, ми деяким чином встановили математичне сподівання попиту на деякий товар. Однак цього замало – треба хоча б оцінити ступінь коливання цього попиту, щоб відповісти на запитання – а яка ймовірність того, що він буде знаходитися в певних межах? От якби встановити факт приналежності даної випадкової величини до нормального класичного розподілу, тоді задача оцінки діапазону, тобто довіри до нього (довірчих інтервалів) була б вирішена без будь-яких труднощів.
Доведено, що, наприклад, з ймовірністю більше 95% випадкова величина X з нормальним законом розподілу лежить у діапазоні, де математичне сподівання Mx дорівнює плюс/мінус три середньоквадратичних відхилення Sх.. Таким чином, справа полягає у тому, до якої із схем випадкових подій класичного зразка ближче всього належить схема функціонування елементів вашої системи.
Наведемо простий приклад. Слід оцінити показники оплати за послуги надання часу на міжміські переговори, наприклад, знайти ймовірність того, що за 1 хвилину здійснюється рівно N переговорів, якщо заздалегідь відомо середнє число замовлень, що надходять за хвилину. Виявляється, що схема таких випадкових подій підпадає під розподіл Пуассона для дискретних випадкових величин. Цьому розподілу підпорядковуються майже усі дискретні величини, що пов’язані з так званими «рідкісними» подіями.
Далеко не завжди математична оболонка класичного закону розподілу досить проста. Навпаки, найчастіше це складний математичний апарат зі своїми, специфічними прийомами. Однак справа не в цьому, тим більше при «суцільній» комп'ютеризації усіх сфер діяльності людини. Очевидно, що немає необхідності знати в деталях властивості всіх або хоча б певної частини класичних розподілів. Досить пам’ятати тільки про саму можливість скористатися ними.
Таким чином, під час системного підходу до розв’язання тієї або іншої задачі керування слід дуже зважено поставитися до вибору елементів системи або окремих її системних операцій. При цьому не завжди «збільшення показників» забезпечить логічну стрункість структури системи, тобто, треба розуміти, що помітити близькість схеми подій у даній системі до схеми класичної найчастіше вдається тільки на «елементарному» рівні системного аналізу.
Завершуючи питання про розподіли випадкових величин звернемо увагу на ще одну важливу обставину - навіть якщо нам досить одного єдиного показника – математичного сподівання деякої випадкової величини, то й у цьому випадку виникає питання щодо надійності даних про цей показник. І справді, нехай даний вибірковий розподіл випадкової величини X, наприклад,  щоденний виторг у $, у вигляді 100 спостережень за цією величиною. Нехай ми розрахували середнє Mx і воно склало $125 за умови коливань від $50 до $200. Разом з тим, припустимо, що було знайдено Sx, що дорівнює $5. Звідси постає запитання – а наскільки правильним буде твердження, що у наступні дні виторг складе $125 або буде знаходитись в інтервалі $120..$130 або виявиться більше деякої суми, наприклад, $90?
Питання такого типу є надзвичайно гострими, особливо якщо це елемент деякої економічної системи (один з багатьох). При цьому висновки за результатами системного аналізу та їх вірогідність, зазвичай, залежать від відповідей на деякі запитання. Що ж говорить теорія про ці питання?
З одного боку, надто багато, а з іншого боку – майже нічого. Так, наприклад, якщо у вас є впевненість у тому, що «теоретичний» розподіл деякої випадкової величини відноситься до деякого класичного, тобто цілком описаного в теорії типу, то можна отримати досить багато корисного. Дійсно:
· за допомогою теорії можна знайти довірчі інтервали для даної випадкової величини. Якщо, наприклад, уже доведено, точніше прийнята гіпотеза про нормальний розподіл, то знаючи середньоквадратичне відхилення можна з впевненістю до 5% вважати, що виявиться поза діапазоном (Mx - 3Sx) ... (Mx+3Sx), або у нашому прикладі про виторг з ймовірністю 0,05 буде < $ 90 або > $ 140. Слід погодитись із своєрідністю теоретичного висновку, за яким стверджується не той факт, що виторг складе від 90 до 140 (з ймовірністю 95%), а тільки те, що сказано вище;
· якщо в нас немає теоретичного підґрунтя, щоб прийняти який-небудь класичний розподіл, що буде придатним для нашої ВВ, то і тут теорія зробить нам послугу, тобто дозволить перевірити гіпотезу про розподіл на підставі наявних у нас даних. Правда, вичерпної відповіді «Так» або «Ні» чекати не слід. Можна лише отримати ймовірність помилки, відкинувши правильну гіпотезу (помилка 1 роду) або ймовірність помилки, прийнявши помилкову гіпотезу (помилка 2 роду);
· навіть такі «обмежені» теоретичні висновки дуже залежать від обсягу вибірки, тобто кількості спостережень, а також від «чистоти проведення експерименту», тобто від умов його проведення.

3.2 Методи непараметричної статистики

Використання класичних розподілів випадкових величин зазвичай називають «параметричною статистикою». При цьому робиться припущення про те, що ВВ (дискретна або неперервна), яка нас цікавить,  має ймовірності, що обчислюються за деякими формулами або алгоритмами. Однак не завжди для цього є підстави. Причинами цього найчастіше є дві:
- деякі випадкові величини просто не мають кількісного опису, тобто обґрунтованих одиниць вимірювання (рівень знань, якість  продукції і под.);
- спостереження за величинами можливі, однак їх кількість надто мала для перевірки припущення (гіпотези) про тип розподілу.
В наш час у прикладній статистиці усе більшою популярністю користуються методи так званої непараметричної статистики, тобто, коли питання про належність розподілу ймовірностей даної величини до того або іншого класу взагалі не розглядається, однак задача оцінювання самої ВВ, тобто отримання інформації про неї, залишається.
Одним з основних понять непараметричної статистики є поняття шкали або процедури шкалування значень ВВ. За своїм змістом така про­цедура шкалування полягає у вирішенні питання про «одиниці вимірю­вання» ВВ. Зазвичай прийнято використовувати чотири типи таких шкал.
Nom - номінальна шкала, тобто шкала, що застосовується до тих величин, що не мають природної одиниці вимірювання. Якщо деяка величина може приймати на своїй номінальній шкалі значення X, Y або Z, то справедливими вважаються тільки вирази типу: (X # Y), (X # Z), (X = Z), у той час як вирази типу (X >Y), (X <Z), (X + Z) не мають ніякого сенсу. Прикладами ВВ, до яких застосовні тільки номінальні шкали можуть бути такі величини, як стать, колір, марка автомобіля і под.
Ord. Другий спосіб шкалування, це використання порядкових шкал. Вони незамінні для ВВ, що не мають природних одиниць вимірювання, однак, вони дозволяють застосовувати поняття переваги одного значення над іншим. Типовий  приклад: оцінювання знань (навіть при нечисловому опису), службові рівні і под. Для таких величин дозволені не лише відношення рівності (= або #), але й знаки переваги ( > або <). Іноді говорять про ранги значень таких величин.
Int & Rel. Це два способи шкалування, що використовуються для ВВ, і які мають натуральні розмірності, тобто інтервальна і відносна шкала. Для таких величин, крім відношень рівності і переваги можуть застосовуватись операції порівняння, тобто, усі чотири дії арифметики. Головна особливість таких шкал полягає у тому, що різниця двох значень, наприклад, на шкалі (36 і 12) має один зміст для будь-якого місця шкали (28 і 4). Розходження між інтервальною шкалою і відносною є тільки у понятті нуля, тобто на інтервальній шкалі 0 кг ваги означає відсутність ваги, а на відносній шкалі температур 0 градусів не означає відсутність теплоти, оскільки, можливі температури, що будуть нижчі 0 градусів за Цельсієм.
Звідси можна помітити ще одну перевагу, яку ми отримуємо під час використання методів непараметричної статистики, тобто, якщо ми стикаємося з ВВ неперервної природи, то використання  інтервальної або відносної шкали дозволить нам мати справу не з випадковими величинами, а з випадковими подіями, тобто типу «ймовірність того, що вага продукції знаходиться в інтервалі 17 кг». Тому можна запропонувати єдиний підхід до опису всіх показників функціонування складної системи – опис на рівні простих випадкових подій (з ймовірністю P(X) може відбутися подія X). При цьому під подією доведеться розуміти те, що випадкова  величина займе одне з можливих для неї положень на шкалі Nom, Ord, Int або Rel.
Зазвичай такий “мікроскопічний” підхід різко збільшує обсяг інформації, що необхідна для системного аналізу. Частково цей недолік пом'якшується при використанні комп'ютерних методів системного аналізу, але більш важливим є інше – перевага на початкових етапах аналізу, коли зважуються питання дезінтеграції великої системи (виділення окремих її елементів) і наступної її інтеграції для розроблення стратегії керування системою.

Не буде перебільшенням вважати, що методи непараметричної статистики – є могутнім засобом під час розв’язання задач системного аналізу у багатьох областях діяльності людини і зокрема в  економіці.

3.3 Кореляція випадкових величин

Прямим означенням терміна кореляція (correlation) є стохастичний, ймовірний і можливий зв'язок між двома (парна) або кількома (множинна) випадковими величинами.
Вище говорилося про те, що якщо для двох ВВ (X і Y) має місце рівність P(XY) = P(X)P(Y), то величини X і Y вважаються незалежними. Однак, якщо це не так? Адже завжди важливим є запитання – а наскільки залежить одна ВВ від іншої? І справа у властивому людям прагненні аналізувати що-небудь обов'язково у числовому вимірі. Зрозуміло, що системний аналіз означає неперервні обчислення, при цьому використання комп'ютера змушує нас працювати з числами, а не поняттями.
Для числового оцінювання можливого зв'язку між двома випадковими  величинами Y (із середнім My і середньоквадратичним відхиленням Sy) та Х (із середнім Mx і середньоквадратичним відхиленням Sx) прийнято використовувати  коефіцієнт кореляції
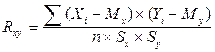.                                  (3.10)
Цей коефіцієнт може набувати значення від -1 до +1 залежно від тісноти зв'язку між даними випадковими величинами. Якщо коефіцієнт кореляції дорівнює нулю, то X і Y називають некорельованими. Вважати їх незалежними зазвичай немає підстав.
Виявляється, що існують такі, як правило, нелінійні зв'язки величин для яких Rxy = 0, хоча величини і залежать одна від одної. Зворотне завжди правильне – якщо величини незалежні, то Rxy = 0. Однак, якщо модуль Rxy = 1, то є всі підстави думати про наявність лінійного зв'язку між X і Y. Саме тому часто говорять про лінійну кореляцію під час застосування такого способу оцінювання зв'язку між ВВ.
Відзначимо ще один спосіб оцінювання кореляційного зв'язку двох випадкових величин. Якщо додати добутки відхилень кожної з них від свого середнього значення, то отриману величину
,                               (3.11)
або коваріацію величин X і Y відрізняє від коефіцієнта кореляції два показники: по-перше, усереднення (ділення на число спостережень або пар X, Y) і, по-друге, нормування шляхом ділення на відповідні середньоквадратичні відхилення. Таке оцінювання зв'язків між ВВ у складній системі є одним з початкових етапів системного аналізу, і тому вже тут постає питання про довіру до висновку про наявність або відсутність зв'язків між двома ВВ.
У сучасних методах системного аналізу зазвичай діють таким чином. За знайденим значенням R обчислюють допоміжну величину
W = 0,5 Ln[(1 + R) / (1-R)], і питання про довіру до коефіцієнта кореляції зводять до довірчих інтервалів випадкової величини W, що визначаються стандартними таблицями або формулами.
В окремих випадках під час системного аналізу доводиться вирішувати питання про зв'язки кількох (більше 2) випадкових величин або питання про множинну кореляцію. Так, наприклад, нехай X, Y і Z – випадкові величини, під час спостереження за якими ми встановили їх середнє Mx, My, Mz і середньоквадратичні відхилення Sx, Sy, Sz. Тоді можна знайти парні коефіцієнти кореляції Rxy, Rxz, Ryz  за наведеною вище формулою. Однак цього явно недостатньо, адже на кожному з трьох етапів ми забували про наявність третьої випадкової величини. Тому у випадках множинного кореляційного аналізу іноді потрібно відшукувати так званні часткові коефіцієнти кореляції, наприклад, оцінка впливу Z на зв'язок між X і Y здійснюється за допомогою коефіцієнта
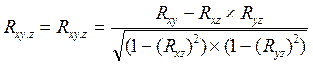.                         (3.12)
І, нарешті, можна поставити запитання. А який же є зв'язок між даною ВВ і сукупністю інших? Відповідь на це дають коефіцієнти множинної кореляції Rx.yz, Ry.zx, Rz.xy, формули для обчислення яких аналогічні тим же принципам, тобто із врахуванням зв'язків однієї з величин із всіма іншими у сукупності.
На складність обчислень всіх описаних показників кореляційних зв'язків можна не звертати особливої уваги. Програми для їх розрахунку досить прості і існують у готовому вигляді у багатьох програмах прикладного забезпечення сучасних комп'ютерів. Достатньо зрозуміти лише головне – якщо для формального опису елементів складної системи, сукупності таких елементів у вигляді підсистеми або системи у цілому, ми розглядаємо зв'язки між окремими її частинами, то ступінь тісноти зв'язків у вигляді впливу однієї ВВ на іншу можна і потрібно оцінювати на рівні кореляції.
Наприкінці відзначимо ще одне. В усіх випадках системного аналізу на кореляційному рівні обидві випадкові величини за умови парної або множинній кореляції вважаються «рівноправними». Тобто, мова йде про взаємний вплив ВВ одна на одну. Так буває далеко не завжди і часто питання про зв'язки X і Y ставиться інакше – тобто чи є одна з величин функцією від іншої величини (аргументу).

3.4 Лінійна регресія

У тих випадках, коли з природи процесів у системі або з даних спостережень над нею випливає висновок про нормальний закон розподілу двох ВВ – X і Y, з яких одна є незалежною, тобто Y є функцією від X, то виникає спокуса визначити таку залежність “формульно”, аналітично. При цьому було б набагато простіше вести системний аналіз – особливо для елементів системи типу «вхід – вихід». Звичайно, найпривабливішою є лінійна залежність типу Y = a + bX. Подібна задача є задачею регресійного аналізу і має такий спосіб розв’язання. Висувається така гіпотеза:
H0 : випадкова величина Y для фіксованого значення величини X розподілена за нормальним законом з математичним сподіванням
My=a+bX,                                              (3.13)
і дисперсією Dy , що не залежить від X.
За наявності результатів спостережень над парами Xi і Yi попередньо обчислюються середні значення My і Mx, а потім здійснюється оцінювання коефіцієнта b у вигляді:
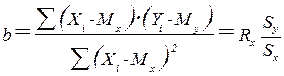,               (3.14)
що випливає з визначення коефіцієнта кореляції за (3.1). Після цього обчислюється оцінка для a у вигляді
a=My- b×Mх,                                  (3.15)
і здійснюється перевірка значимості отриманих результатів. Таким чином, регресійний аналіз є потужним, хоча і далеко не завжди доступним розширенням кореляційного аналізу, розв’язуючи усе ту ж задачу оцінювання зв'язків у складній системі.

3.5 Елементи теорії статистичних рішень

Що таке – статистичне рішення? Як найпростіший приклад розглянемо ситуацію, у якій треба зіграти у таку гру:
· вам заплатять 2 долари, якщо підкинута монета впаде догори гербом;
· ви заплатите 1 долар, якщо вона впаде гербом униз.
Швидше за все, ви погодитеся зіграти, хоча розумієте ступінь ризику. Ви усвідомлюєте, «знаєте» про рівноймовірні появи герба і «обчислюєте» свій виграш  0,5×2 - 0,5·1=+$0,5.
Ускладнимо цю гру. Ви бачите, що монета трохи вигнута і можливо буде падати частіше однією зі сторін. Тепер рішення грати або не грати як і раніше залежить від ймовірності виграшу, що не може бути заздалегідь (по-латинському – apriori) прийнята рівною 0,5.
Людина, що знайома із статистикою, спробує оцінити цю ймовірність за допомогою дослідів, якщо зазвичай вони можливі і коштують не дуже дорого. Звідси виникає запитання – скільки таких підкидань вам буде досить?
Нехай ви платите 5 центів за одне експериментальне підкидання, а ставки у грі складають $2000 проти $1000. Швидше за все ви погодитесь грати, заплативши порівняно невелику суму за 100..200 експериментальних підкидань. Ви напевно будете  вести  підрахунок вдалих падінь і, якщо їх число складе 20 з 100, припините експеримент і зіграєте на ставку $2000 проти $1000, оскільки очікуваний виграш оцінюється у 0,8×2000 + 0,2×1000 - 100×0,05 = $1795.
У наведених прикладах головним для прийняття рішення була ймовірність успішного результату падіння монети. У першому випадку – апріорна ймовірність, а у другому – апостеріорна. Таку інформацію прийнято називати даними про стан природи.
Наведені приклади мають безпосереднє відношення до сутності нашого предмета. І справді – під час системного керування доводиться приймати  рішення в умовах, коли наслідки таких рішень заздалегідь вірогідно невідомі. При цьому питання: грати чи не грати – не стоїть! «Грати» треба, тобто треба керувати системою. Ви запитаєте – а як же заборона на експерименти? Відповідь можна дати таку – сама поведінка системи у звичайному її стані може розглядатися як експеримент, з якого для правильної організації збирання та оброблення інформації про поведінку системи можна чекати на одержання даних для з'ясування особливості системного підходу до розв’язання задач керування.
Для детальнішого розуміння теорії статистичних рішень розглянемо такий приклад. Нехай для характеристики об’єктів використовується ознака х, а уся їх сукупність розбита на два класиW1 і W2 [10]. При цьому вважатимемо, що відомі описи цих класів, тобто відомі умовні щільності розподілу ймовірностей f1 (x) і f2 (x) значень ознаки об’єктів класів W1 і W2, а також апріорні ймовірності P(W1) і P(W2) появи об’єктів.
Нехай за результатами експерименту визначено значення ознаки х0 досліджуваного об’єкта (рис. 3.2).

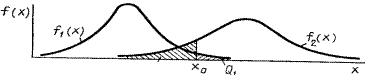
Рисунок 3.2 – Розподіл об’єктів двох класів за ознакою х

Щоб прийняти рішення до якого класу віднести досліджуваний об’єкт, позначимочерез х0 деяке доки ще невизначене значення ознаки х0, і домовимося про таке правило. Якщо значення ознаки задовольняє умову  х0 >х0 , то об’єкт відносимо до класу W2, а якщо задовольняється умова  x0 £ х0 , - то до класу W1.
При цьому, якщо об’єкт відноситься до класу W1, а його вважають об’єктом класу W2, то це свідчить про помилку прийняття рішення - помилка першого роду, умовна ймовірність якої визначається за виразом
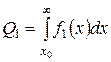.                                                (3.16)
Відповідно до термінології теорії статистичних рішень у цьому випадку помилково вибрана гіпотеза H2, у той час коли правильною є гіпотеза Н1. І навпаки, коли правильною є гіпотеза Н2, а віддана перевага гіпотезі H1, то вчинена помилка другого роду, умовна ймовірність якої визначається як
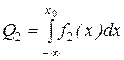.                                                 (3.17)
Умовні ймовірності правильних рішень для випадків справедливості гіпотез H1 і H2 визначаються як:
;
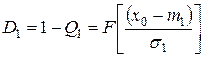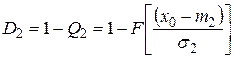,                (3.18)
де D1 – визначає  розмірність іспитів, a D2  – їх потужність.
Міркування, якими слід керуватися під час вибору значення ознаки хо (розбиття простору ознаки х на півпростори R1 і R2) повинні враховувати втрати, що пов’язані з правильними і помилковими рішеннями. Ці втрати зазвичай описують у вигляді платіжної матриці
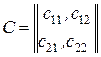,                             (3.19)
де с11 і с22, с12 і с21 – втрати, що пов’язані відповідно з правильними рішеннями і помилками першого і другого виду.
При цьому, у випадку багатократного застосування задачі прийняття рішень, середній ризик буде дорівнювати сумі втрат, що пов’язані з неправильними і правильними рішеннями, з урахуванням ймовірностей їх появи і апріорних ймовірностей появи об’єктів класів W1 і W2
.    (3.20)
Підставляючи у (3.20) вирази (3.16) і (3.17), отримаємо

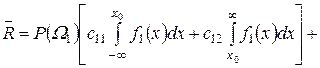
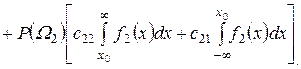.            (3.21)
Оскільки прийняття рішень практично завжди є задачею багатократного застосування, значення  хо слід вибирати таким чином, щоб значення середнього ризику буломінімальним. Щоб визначити значення х0 , для якого середній ризик буде мінімальним, знайдемо його диференціал за х і прирівняємо отриману похідну до нуля, поклавши що  х=х0
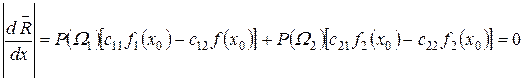,      (3.22)
звідки можна записати, що
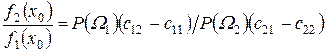.                   (3.23)
Відношення умовних щільностей розподілу f2(x)/f1(x) =l(х) називають коефіцієнтом або відношенням правдоподібності (plausibilityrate). При цьому права частина виразу (3.23)
              (3.24)
визначає порогове (критичне) значення коефіцієнта правдоподібності.
Значення хо дозволяє оптимально (з точки зору мінімуму середнього ризику) розбити простір значень ознаки х на області R1 і R2. Область R1 включає значення  х £  х0, для якихl(x) £l0 , а область R2 – значення  х > х0 , для якихl(x) > l0 .Тому рішення про віднесення досліджуваного об’єкта до класу W1 слід приймати, якщо значення коефіцієнта правдоподібності менше або дорівнює його критичному значенню. Інакше, об’єкт слід віднести до класуW2.
У загальному випадку, коли число класів m > 2, а об’єкти описуються набором ознак  x1,..., хN  або вектором x = { x1,..., хN}, відношення правдоподібності між класамиW k іW l  буде визначатися як
lkl= fk (х)/fl (х),  k,l=1,..., m,                             (3.25)
платіжна матриця має вигляд
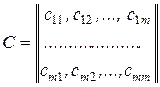,                                             (3.26)
а середній ризик обчислюється за виразом
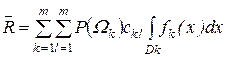.                           (3.27)
З умови мінімуму значення середнього ризику рівняння границь у багатовимірному просторі ознак між областями Dk і Dl, що відповідають класамWk іW l , буде визначатися як
.  (3.28)
При цьому, якщо покласти, що ckk = cll= 0, a ckl = clk = 1, то будемо мати:

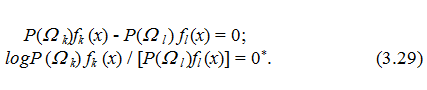
3.5.1 Критерій Байєса

Критерій Байєса (Bayesiancriterion) – правило, за яким стратегія прийняття рішень вибирається таким чином, щоб забезпечити мінімум середнього ризику. Застосування критерію Байєса доцільне для систем багатократного розпізнавання в умовах незмінного простору ознак, незмінного опису класів і незмінної платіжної матриці.
З теорії статистичних рішень відомо, що мінімум середнього ризику забезпечується тільки тоді, коли рішення про віднесення об’єктів до класів W1 або W2 приймаються за правилом: якщо виміряне значення ознаки об’єкта знаходиться в області R1, то об’єкт відносять до класу W1, а якщо це значення знаходиться в області R2 – до класу W3.
Стратегію і мінімальний середній ризик, що визначаються за таким правилом, називають байєсівськими.
Байєсівска стратегія може бути описана також і таким чином. Нехай за результатами дослідів встановлено, що значення ознаки об’єкта визначається як х = х0. Тоді умовна ймовірність приналежності об’єкта до класу W1 (умовна ймовірність першої гіпотези) згідно з теоремою гіпотез або формулою Байєса визначиться як
,                       (3.30)
а умовна ймовірність приналежності об’єкта класу W2 (умовна ймовірність другої гіпотези) – як
,                      (3.31)
де  f (x0) = P (W1) f1 (x0) + P (W2) f2 (x0) – спільна щільність розподілу ймовірностей значень ознаки х за класами;
P(W1| х0) і Р(W2| х0) – апостеріорні ймовірності того, що досліджуваний об’єкт належить класам W1 і W2 , відповідно.
При цьому умовні ризики, що пов’язані з рішеннями w ÎW1 і wÎW2, будуть визначатися як
              (3.32)
Система розпізнавання за байєсівською стратегією повинна розв’язу­вати задачу з мінімальним умовним ризиком. Це означає, що перевагу рішенню wÎW1 слід віддавати тільки тоді, коли виконується умова
[R (W1 êx0) / R(W2êx0)] < 1.                           (3.33)
Підставимо у цей вираз значення R (W1 êx0)і R (W2 êx0), що визначені за (3.32). Тоді нерівності
c1R(W1êx0) >c2R(W2êx0),
або
[R (W1 êx0) / R (W2 êx0)]> c2/c1                   (3.34)
будуть визначати умови, за якими слід приймати рішення, що wÎW1.
Таким чином, байєсівський підхід до розв’язання задачі прийняття рішення полягає в обчисленні умовних апостеріорних ймовірностей і порівняння їх значень. Саме це і забезпечує мінімум середнього ризику, а значить і помилкових рішень. Узагальнюючи вищеописане для числа варіантів рішень т>2, апостеріорна ймовірність віднесення об’єкта до класу W і буде визначатися як
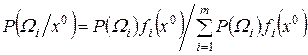.                (3.35)
При цьому, якщо об’єкт або система до того ж характеризуєтьсяознаками xj, j =, і ці ознаки прийняли значення х1 = х10, x2 = x20,..., xn = xN0, ймовірність того, що за умови появи події An= (x10, х20,..., xN0), об’єкт відноситься до i-го класу дорівнює
P(Wi½AN) = [P(Wi)fi(x10, x20,..., xn0)] / Sm P(Wi)fi(x10, x20,..., xn0).  (3.36)
Розглянемо ще одну форму запису байесівського критерію віднесення об’єкта до відповідного класу. Нехай є класи W1 і W2 . Апріорні ймовірності появи об’єктів цих класів будуть відповідно P(W1) і P(W2), с11 = с22 = 0, с12 = c1 і c21 = c2 . Відомі також багатомірні умовні щільності розподілу ймовірностей значень ознак¦1(x1,..., хn) і f2(х1,..., хn) за класами. Тоді умовні ймовірності помилок першого і другого роду будуть визначатися як:
Q1 = òR2...ò¦1(x1,..., xn)dx1,..., dxn ,  Q2 = òR1...ò¦2(x1,...,xn)dx1,..., dxn .  (3.37)
Середній ризик, при цьому буде визначатись за виразом
.                        (3.38)
Оскільки інтеграл від щільності розподілу ймовірності по областях R1 і R2 дорівнює одиниці, то  Q1=1- ò...ò f1(x1...xn)dx1,....dxn , звідки
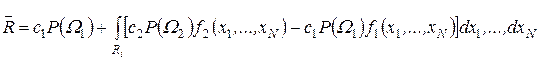. (3.39)
Задача полягає у тому, щоб мінімізувати значення середнього ризику. Для цього необхідно так вибрати області Ri і Рч, щоб інтеграл у (3.39) прийняв найбільше від’ємне значення. Це досягається тоді, коли вираз під інтегралом приймає найбільше від’ємне значення і поза областю Ri не існує такої області, де вираз під інтегралом буде від’ємним, тобто
c2P(W2) f2(x1,..., хт) - c2P(W1) f1(x1,..., хn) < 0.                   (3.40)
Звідси випливає вже відоме правило прийняття рішень. Досліджуваний об’єкт, ознаки якого, як встановлено за результатами експерименту, дорівнюють х1 = х10, x2 = х20,..., хn = х0n , то відноситься до класу W1, якщо
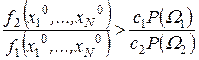,                            (3.41)
де c1 Р(W1)/с2 P(W2) = lo - порогове значення коефіцієнта правдоподібності.

3.5.2 Мінімаксний критерій

На практиці можливі такі ситуації, коли апріорні ймовірності появи об’єктів відповідних класів невідомі. У цьому випадку мінімізувати значення середнього ризику прийняття рішень за байєсівською стратегією не вдається. У цій ситуації доцільно використовувати критерій, що мінімізує максимально можливе значення середнього ризику (мінімаксний критерій).
Мінімаксна стратегія полягає у тому, що рішення про приналежність об’єкта відповідному класу приймається на основі байєсівської стратегії, що відповідає такому значенню P(Wi), для якого середній ризик  буде максимальним. Покажемо перевагу мінімаксної стратегії у порівнянні з іншими в умовах, коли невідомі значення  P(W і), і = 1,..., m.
За наявності класівW1 і W2 байєсівський ризик з урахуванням того, що Р(W2) = 1-P(W1),  с11 = с22 = 0, a c12 = с1 і с12 = с2, рівні
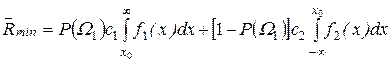.                    (3.42)
Побудуємо графік функції Rmin=f [P(W1)], пам'ятаючи при цьому, що для P(W1) = 0 і P(W1) = 1  Rmin = 0  (рис. 3.3).

     

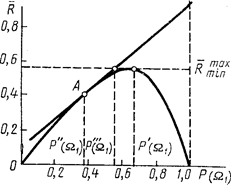
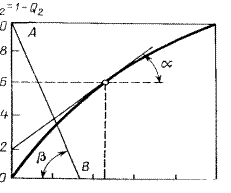
Рисунок 3.3 – Графік функції                           Рисунок 3.4 – Характеристика
 Rmin=f [P(W1)]
Нехай Rmin досягає свого найбільшого значення при P(W1) = P'(W1). Цей ризик дає максимальне значення мінімального байєсівського ризику (позначимо його як Rminmax). Застосування мінімаксного критерію означає, що за відсутності даних щодо апріорних ймовірностей появи об’єктів слід орієнтуватися на P(W1)=P'(W1), а середні втрати визначаються дотичною до кривої R=f[P(W1)] у точці P'(W1).
Для визначення алгоритму прийняття рішення відповідно мінімаксній стратегії, продиференціюємо (3.42) за P(W1) і прирівняємо цю похідну до нуля. У результаті отримаємо
c1Q1(x0) = c2Q2(x0).                               (3.43)
Це співвідношення, що описує рівність умовних значень середніх ризиків при помилках першого і другого роду, дозволяє визначити х0 і побудувати такий алгоритм класифікації. Якщо значення ознаки х об’єкта w дорівнює х0, то w ÎW1 якщо х = х0£ х0, іw Î W 2  якщо х = х0 > х0.
Мінімаксна стратегія, що пропонує значення P(W1) = P'(W1), дає порогове значення коефіцієнта правдоподібності
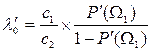.                                      (3.44)
Визначення  дозволяє записати алгоритм класифікації у вигляді: wÎW1 , якщоl(x) £   і  w Î W2, якщоl(x) > . При цьому, якщо с1 = с2 , то мінімаксна стратегія призводить до рівності умовних ймовірностей помилок першого і другого роду.
На завершення відзначимо, що мінімаксна стратегія є байєсівською стратегією для найгірших значень апріорних ймовірностей, що дасть хоча і обережне, але гарантоване значення середнього ризику.

3.5.3 Критерій Неймана-Пірсона

На практиці часто буває, що можуть бути невідомі не тільки апріорні ймовірності появи об’єктів відповідних класів, але й платіжні матриці. У таких системах для побудови алгоритму класифікації доцільно скористатися критерієм Неймана - Пірсона, суть якого полягає у такому.
Виходячи з того, що рішення приймаються за результатами експерименту над об’єктами, визначається допустиме (задане) значення умовної ймовірності помилки першого роду, а після цього визначається така границя між класами прийняття рішень, дотримуючись якої вдається досягти мінімуму умовної ймовірності помилки другого роду.
Нехай з деяких міркувань прийнято рішення, що допустима умовна ймовірність помилки першого роду не повинна перевищувати деякої сталої величини . Треба визначити х0 для задачі  за обмежень типу. Oчeвидно, що рішення хо задовольняє рівняння ,оскільки для значення умовна ймовірність помилок другого роду Q2 зростає. Обрати ж  значення << не можна за умовою задачі.
На завершення розглянемо геометричну інтерпретацію вищевказаних критеріїв. Для цього в координатах і Qi побудуємо характеристику (рис. 3.4), відзначаючи що для Q1 = 0 Q2 = 1 і D2 = 0, і навпаки, для Q1 = l Q2 = 0 і D2 = l. Оскільки , a , то продиференціювавши D2 за Q1, отримаємо, що
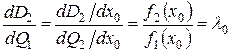.                      (3.45)
Однак диференціал dD2/dQ1 є тангенсом кута нахилу дотичної до робочої характеристики дляl = lо. Тому для визначення Q1 і D1 на основі застосування критерію Байєса на робочій характеристиці знайдемо точку, дотична у якій має нахил, що дорівнюєlо = [Р(W1) с1/Р(W2) с2], тобто . Тепер ордината цієї точки визначає умовну ймовірність правильного рішення, а абсциса – означає умовну ймовірність помилки першого роду.
Для визначення Q1 і D2 за мінімаксним критерієм необхідно враховувати, що похідна від середнього ризику за апріорною ймовірністю P(W1) у точці його максимуму дорівнює нулю. Оскільки
R= c11P(W1)(l -Q1)+с12P(W1)Q1+с22[1-P(W1)]D2+c21[l-P(W1)](1-D2),    (3.46)
тo
дR/дP(W1) = c11 (1-Ql)+c12Q1 - c22D2 - c21(1-D2) =0.            (3.47)
В координатах Q1 і Q2 це рівняння прямої і якщо с11 = с22, то
D2 = Q1[c11 - c12)/(c21 - c22)]+1                          (3.48)
з кутовим коефіцієнтом g  = tgb = [(c11-с12)/(c21-с22)]+1.
Проведемо на графіку (рис. 3.4) цю пряму АВ. Координати точки перетину цієї прямої з робочою характеристикою визначають умовні ймовірності Q1 і D2 = 1-Q2 в умовах застосування мінімаксного критерію. Тангенс кута нахилу дотичної у цій точці дорівнює lо.

3.5.4 Критерій послідовних рішень

Раніше припускалося, що рішення про належність об’єкта, що розпізнається, відповідному класу, приймається після вимірювання усієї сукупності ознак об’єкта x1,...,хn. Однак можливий й інший підхід до розв’язання цієї задачі: після вимірювання кожної чергової ознаки х1; х1, х2; х1, х2, х3  і т. д. включається алгоритм розпізнавання і розв’язується задача прийняття рішення на основі даних про виміряні до поточного моменту ознаки досліджуваного об’єкта. При цьому залежно від результатів порівняння отриманих значень з деякими встановленими заздалегідь границями або вимірюється чергова ознака об’єкта w, або припиняється подальше накопичення інформації про об’єкт. Така процедура розв’язання задачі прийняття рішень, що називається послідовною, зобов'язана своїм виникненням одному з розділів статистики – послідовному аналізу [7, 20].
Послідовне і багатократне розв’язання задачі прийняття рішень з використанням на кожнім кроці усе зростаючого числа виміряних ознак особливо доцільно у випадках, коли визначення ознак пов’язано із витратами на проведення експериментів (процес накопичення експериментальних даних вимагає витрат значної кількості годин, проведення експериментів пов’язано з певним ризиком (наприклад, при порушенні медичного діагнозу), об’єкти ряду класів з їх загальної сукупності надійно розпізнаються за обмеженою кількістю ознак. Розглянемо сутність послідовної процедури прийняття рішень.
Нехай множина прийняття рішень розділена на класи Qi, при цьому робочий словник містить ознаки х1,...,хn і функції умовної щільності розподілу ймовірностей будуть fі (x1); fi (x1, x2); ...; fi (x1,...,x4,), i = l, 3.
Припустимо, що проведено серію з п експериментів, у результаті яких визначено ознаки х1,...,хп (n<N). Зіставимо відношення n-мірних функцій умовних щільностей розподілу ймовірностейln=f1(x1,..., xn)/f2(x1,...,хп) з величиною А і В. При цьому будемо враховувати таке: якщоlп ³ А, то проведення експериментів припиняється і приймається рішення про те, що wÎW1, а якщоlп £ В, то проведення експериментів також припиняється і приймається рішення про те, що w Î W2. Якщо ж  В < хп < А, то приймається рішення, що експерименти необхідно продовжити і визначається чергова (п + 1)-а ознака досліджуваного об’єкта.
Сталі А і В, що називаються верхнім і нижнім порогом, можуть бути визначені з таких міркувань. Нехай після вимірювання п ознакln = А, тоді позначимо 'xn'={x1,...,хп}, і отримаємо fi(xn)=Af2(хn) або
Gіò¦1(xn)dxn = Aò¦2(xn)dxn ,                              (3.49)
де Gi – область простору ознак щодо класу W1.
За визначенням умовної ймовірності помилок першого і другого роду можна записати, що  l-Q1=AQ2. Аналогічні міркування приводять до співвідношення Q1 = B(1-Q2). Звідси, у загальному випадку
А £ [(1-Q1)/Q2],   B ³ [Q1/(l-Q2)].                            (3.50)
Таким чином, для визначення порогів А і В необхідно задатися допустимими значеннями помилок першого і другого роду.
Якщо число класів прийняття рішень m > 2, то послідовна процедура полягає у такому. Виходячи з того, що рішення будуть прийматися після розпізнавання невідомих об’єктів, задаються допустимі значення ймовірностей правильних (eii) і помилкових(eiq) рішень, що дозволяє визначити значення порогів для кожного класу, тобто
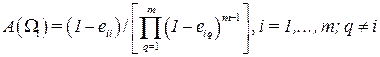.          (3.51)
Нехай у результаті проведення деякої сукупності експериментів визначено вектор ознак хn={Х10,..., xn0} і розраховано відношення ймовірностей
ln(Xn0½W i) = fi(Xn0) [q=1Õm¦n0(Xn0)]m-1.          (3.52)
Зіставимо ln(Xn0½Wi) з відповідним порогом А(Wі) , i=1,...,m. Якщоln(Xn0½Wi) < A (Wі), то приймається рішення про те, що w Î Wі. Якщо ж наявність апостеріорної інформації про знайдені ознаки не дозволяє виключити всі класи, окрім одного, то здійснюється наступний експеримент з метою визначення ознаки хп+1. Після цього визначається ln+1(xn + 10½Wi) і здійснюється його порівняння з порогом А(Wі). Якщо при цьому знов не вдається встановити, що об’єкт відноситься саме до даного класу, то приймається рішення провести черговий експеримент з метою визначення ознаки хn+2.
Подібна процедура послідовного знаходження ознак – визначення коефіцієнта правдоподібності l1(x10/Wi),..., ln(Xn0/Wi) і зіставлення його значення з порогом А(Wі) здійснюється до тих пір, доки послідовним виключенням не вдасться прийняти рішення про належність об’єкта саме до цього класу.

3.5.5 Регуляризація задачі прийняття рішень

Відповідно до стратегії Байєса, якщо у досліджуваного об’єкта (системи) виміряне значення ознаки х = х0, то w Î W1 при х0 £ х0 і w Î W2 при х0 > х0. Хоча розв’язання х = х0 і забезпечує мінімум середнього (байєсівського) ризику, тобто, R(x0) = min(х), таке правило прийняття рішень за наявності помилок вимірювання є нестійким.
Якщо значення ознаки х вимірюється з деякою точністю¶х, то для діапазону його модифікації (хо - ¶х, хо + х) рішення, що приймається за значенням х = х0 (вибраний клас), може відрізнятися від того, що відповідає істинному значенню ознаки х. Тому область значень ознаки (хо - ¶х, хо + х) може бути названа областю нестійкості стратегії мінімізації середнього ризику (стратегії Байєса).
Загальний підхід до некоректних задач, що мають нестійкі рішення, запропоновано академіком А. Н. Тихоновим, що полягає у їх регулюванні, тобто у такій модифікації, за якою знову отримана задача є близькою до вихідної і характеризується властивістю тривалості. Щодо даної задачі системного аналізу цей підхід можна реалізувати таким чином.
Трансформуємо вищенаведене правило прийняття рішень таким чином, щоб в межах зони нестійкості (хо - ¶х, хо + х) алгоритм відмовляється від прийняття будь-якого рішення. За зоною нестійкості, якщо виміряне значення ознакидорівнює х = х0, то приймається рішення w Î W1 при х0  £ хо - ¶х аборішення w Î W2 при х0 > хо + х.
Використання такого алгоритму виключає нестійкі рішення задачі за рахунок того, що з'являються такі значення ознаки х = х ± х, в межах яких алгоритм не дає відповіді на запитання про те, до якого класу слід віднести досліджуваний об’єкт або систему.
Регуляризація задачі прийняття рішень приводить до того, що зменшуються помилки першого і другого роду:
;
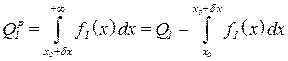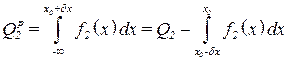,              (3.53)
а також зменшується і регуляризоване значення середнього байєсівського ризику:
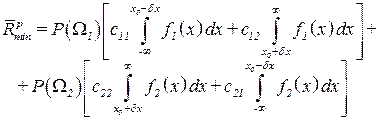.             (3.54)
При цьому
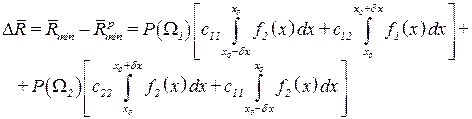.        (3.55)
Оцінимо ймовірність відмови системи від встановлення класу, до якого можна віднести досліджуваний об’єкт або систему. Ця ймовірність відмови
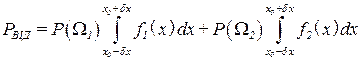          (3.56)
залежить безпосередньо від точності вимірювання досліджуваної ознаки.
Очевидно, що слід намагатись по можливості мінімізувати область нестійкості стратегії Байєса. Це може бути досягнуто за рахунок зменшення величини dхj, j =1,...,N. Однак у загальному випадку це пов’язано із збільшен­ням витрат ресурсів, величина яких не може бути необмеженою. При цьому виникає запитання – точність якого  вимірювача слід підвищувати?
Як показано у [19], інформативність ознак – це величина не абсолютна, а умовна. Тому відповіді на поставлене запитання, напевне, не існує. Однак евристична рекомендації прикладного характеру можуть полягати у такому. Передусім необхідно знайти найінформативнішу ознаку робочого словника ознак у припущенні, що він визначається на першій стадії експериментів. Доцільно забезпечити максимально можливу точність вимірювання цієї ознаки (наприклад хl, l =1,...,N). Далі слід визначити таку ознаку хk, k = l,..., N, k ¹l, вимірювання якої вносить у системний аналіз найбільшу кількість інформації у припущенні, що на попередньому кроці визначено ознаку хj , тобто j = mах I (xjl½xi).
У цьому рівнянні кількість інформації підраховують для усіх можливих значень ознак хk, хl, хj, k, I, j= l,..., N, k¹ l¹ j. Після цього процедура повторюється, тобто визначають I (xr½xk, xl) = maxj I (xj½xk xl), r, k, l, =1,...,N, k¹ l¹ j ¹ r.
Як правило, визначення вже декількох ознак виявляється достатнім для вирішення запитання, що нас цікавить. Саме між вимірювачами, що призначені для визначення ознак xl, xk, хr, доцільно розподілити основну частину ресурсів, що призначені для апаратурного забезпечення системного аналізу. При цьому слід підвищувати їх точнісні характеристики, що забезпечить, у свою чергу, зменшення області нестійких рішень під час використання цих ознак.

Запитання і завдання для самоконтролю

  • Назвіть основні поняття, що використовуються в задачах математичної статистики.
  • Дайте означення основних характеристик випадкових подій і величин.
  • Які закони розподілу випадкових величин Ви знаєте? Які використовуються в задачах СА?
  • При якому розподілі випадкової величини розсіювання її значень буде найбільшим?.
  • В яких випадках використовується формула Байєса при розгляді випадкових подій?
  • Поясніть різницю між параметричною і непараметричною статистикою?
  • В чому полягає процедура шкалування і які бувають способи шкалування?
  • Дайте означення терміна „кореляція”.
  • Що таке коефіцієнт кореляції і які значення він може приймати?
  • Дайте означення терміна„коваріація”.
  • В чому полягає задача регресійного аналізу?
  • Що таке статистичне рішення?
  • Що такепомилка першого та другого роду при прийнятті рішень?
  • Охарактеризуйте критерій Байєса.
  • У чому полягає мінімаксна стратегія?
  • У чому полягає суть критерія Неймана - Пірсона?
  • У чому полягає послідовна процедура розв’язання задачі прийняття рішень?
  • У чому полягаєрегуляризація задачі прийняття рішень?