4. МОДЕЛЮВАННЯ СИСТЕМ МАСОВОГО ОБСЛУГОВУВАННЯ

4.1 Введення у теорію систем масового обслуговування

Більшість систем, з якими людина має справу, є стохастичними системами. Спроба їх математичного опису за допомогою детермінованих моделей приводить до надто грубої оцінки реальності. Під час розв’язання задач аналізу і проектування таких систем необхідно враховувати те, що випадковість є визначальною у процесах, що протікають в них. При цьому нехтування цією випадковістю (спроба “утиснути” ці задачі у детерміновані рамки) призводить до помилок у висновках і практичних рекомендаціях.
Перші задачі теорії систем масового обслуговування (ТСМО) були розглянуті співробітником Копенгагенської телефонної компанії, датським вченим А. К. Ерлангом у період між 1908 і 1922р. Ці задачі були викликані намаганням упорядкувати роботу телефонної мережі і розробити методи, що дозволяють заздалегідь підвищити якість обслуговування залежно від числа наявних пристроїв. Виявилося, що ситуації, які виникають на телефонних станціях, є типовими не тільки для телефонного зв'язку. Наприклад, робота аеродромів, морських портів, магазинів, термінальних класів, електронних обчислювальних комплексів і т. д. може бути описана у рамках ТСМО. Наведемо деякі приклади систем масового обслуговування.
Приклад 1. Телефонний зв'язок часів Ерланга був телефонною станцією, що була зв'язана з великим числом абонентів. Телефоністки станції в міру надходження викликів з'єднували телефонні номери між собою.
Задача. Яка кількість телефоністок (за умови їх повної зайнятості) повинна працювати для того, щоб втрати заявок були мінімальними?
Приклад 2. Система швидкої допомоги міського району є пунктом, що приймає виклики на виконання, тобто виклики на деяку кількість машин швидкої допомоги і кілька лікарських бригад.
Задача. Визначити кількість лікарів, допоміжного персоналу, автомашин, для того, щоб час очікування виклику був для хворих оптимальним за умови мінімізації витрат на експлуатацію системи і максимізації якості обслуговування.
Приклад 3. Система оброблення інформації містить мультиплексний канал і кілька ЕОМ. Сигнали від датчиків надходять на мультиплексний канал, де вони буферизуються та обробляються, а потім надходять на ту ЕОМ, де черга мінімальна.
Задача. Забезпечити прискорення оброблення сигналів при заданій сумарній довжині черги.
Приклад 4. На рис.4.1 зображена структурна схема типової системи масового обслуговування – ремонтного підприємства (наприклад, ремонт ПЕОМ). Порядок її роботи зрозумілий зі схеми і не потребує роз'яснень.


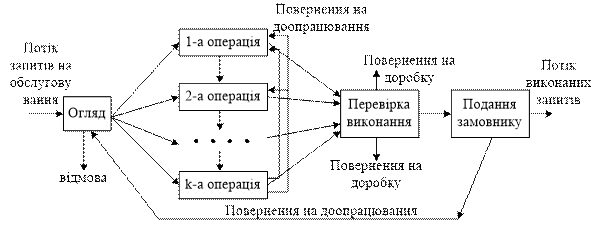
Рисунок 4.1 – Структурна схема типової системи
масового обслуговування

Неважко навести і багато інших прикладів з будь-яких областей діяльності. Характерним для таких задач є:
- умови “подвійної” випадковості – випадковий момент часу надходження замовлення на обслуговування (на телефонну станцію, на пункт швидкої допомоги, на вхід процесора і т. д.) та випадкова тривалість часу обслуговування;
- проблема черги, наприклад, суден перед шлюзами, покупців перед прилавками, задач на вході процесорів обчислювального комплексу і т. д.
А. К. Ерланг звернув увагу на те, що СМО можуть бути поділені на два типи, до яких відносяться системи з очікуванням і системи з втратами. У першому випадку – заявка, що надійшла на вхід системи очікує черги на виконання, а у другому – вона через зайнятість каналу обслуговування одержує відмову і втрачається для СМО. Надалі ми побачимо, що до класичних задач Ерланга додаються нові задачі, а саме:

  • заявки на обслуговування приймаються доти, поки черга не досягне заданого розміру;
  • заявки залишаються у черзі, але очікують обслуговування не більше заданого часу t, після чого з черги виключаються;
  • час очікування обслуговування і час самого обслуговування обмежується деякою величиною t  і т. д.

Реальні системи, з якими приходиться мати справу на практиці, як правило, надто складні і містять у собі ряд етапів (стадій) обслуговування. Причому, на кожному з етапів може існувати ймовірність відмови у виконанні або існує ситуація пріоритетного обслуговування щодо інших заявок. При цьому окремі ланки обслуговування можуть припинити роботу (для ремонту, налагодження і под.) або можуть бути підключені додаткові засоби. Можуть бути і такі обставини, коли заявки, що одержали відмову, знову повертаються у систему, наприклад, в інформаційних системах.
У загальному випадку всі СМО мають цілком визначену структуру, що наведена на рис. 4.2.


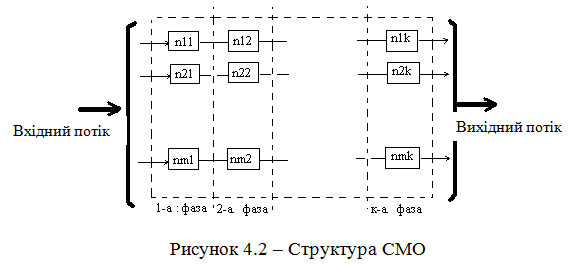
При цьому:

  • потоком називають послідовність подій. Потік, що складається з заявок на обслуговування, називають потоком заявок;
  • потік заявок, що надходять у систему, називають вхідним потоком;
  • потік заявок, що обслуговані, називають вихідним потоком;
  • сукупність черг і приладів (каналів) обслуговування називаються системою обслуговування;
  • кожні заявки надходять на свій канал, де піддаються операції обслуговування;

кожна СМО має певні правила формування черги і правила або дисципліну обслуговування

4.2 Класифікація систем масового обслуговування

За характером заявок розрізняють СМО із скінченною і нескінченною кількістю заявок на вході.
У першому випадку у системі циркулює скінченна, зазвичай постійна кількість заявок, а у другому – деяке джерело генерує нескінченне число заявок. Перші СМО називають замкненими, а другі – розімкненими.
СМО також розрізняють
За дисципліною обслуговування:
- обслуговування у порядку надходження;
- обслуговування у випадковому порядку (відповідно до заданого закону розподілу);
- обслуговування з пріоритетом.
За характером організації:
- з відмовами;
- з очікуванням;
- з обмеженням на очікування.
У першому випадку заявка отримує відмову, коли канал зайнятий. У другому – ставиться у чергу і чекає звільнення каналу. У третьому –випадку вводиться обмеження на тривалість очікування.
За кількістю одиниць обслуговування:
- одноканальні;
- багатоканальні.
За числом етапів (фаз) обслуговування - однофазні і багатофазні (прикладом багатофазних може бути будь-яка потокова лінія).
За властивостями каналів - однорідні, коли канали мають однакову характеристику і неоднорідні у іншому випадку.

4.3 Основна задача теорії систем масового обслуговування

Основна задача ТСМО полягає у встановленні залежності між характером потоку заявок на вході СМО, продуктивністю одного каналу, числом каналів і ефективністю обслуговування. При цьому критеріями ефективності СМО можуть бути різні функції і величини:

  • середній час простою системи;
  • середній час очікування у черзі;
  • закон розподілу тривалості очікування заявки у черзі;
  • середній відсоток заявок, яким відмовили і т. д.

Вибір критеріїв залежить від виду системи. Наприклад:
- для систем з відмовами головною характеристикою є абсолютна пропускна здатність СМО; менш важливі критерії - число зайнятих каналів, середній відносний час простою одного каналу і системи в цілому;
- для систем без втрат(з необмеженим очікуванням) найважливішим є середній час простою у черзі, середнє число заявок у черзі, середній час перебування заявок у системі, коефіцієнт простою і коефіцієнт завантаження системи.
Сучасна ТСМО є сукупністю аналітичних методів дослідження перерахованих різновидів СМО. Надалі з усіх досить складних і цікавих методів розв’язування задач масового обслуговування будуть викладені методи, описувані в класі марковських процесів типу “загибель і розмноження”. Це пояснюється тим, що саме ці методи найчастіше використовуються в практиці інженерних розрахунків.

4.4 Математичні моделі потоків подій

4.4.1 Регулярні і випадкові потоки

Одним з центральних питань організації СМО є з'ясування закономірностей, яким підкоряються моменти надходження в систему заявок на обслуговування. Розглянемо найуживаніші математичні моделі потоків.
Означення.Потік заявок називають однорідним (homogeneousstreamofrequests), якщо він задовольняє умови:

  • усі заявки потоку з точки зору обслуговування є рівноправними;
  • замість заявок (подій) потоку, що за своєю природою можуть бути різними, розглядаються тільки моменти їх надходження.

Означення. Регулярним (regularstreamofrequests) називаються потік, якщо події у потоці випливають одна за одною через конкретні інтервали часу.
Функція f(х) щільності розподілу ймовірності випадкової величини Т – інтервалу часу між подіями має при цьому вигляд:
,                                         (4.1)
де  d - дельта функція,
МТ  - математичне сподівання, причому МТ = Т, дисперсія DТ = 0, а інтенсивність настання подій у потоці t =1/MТ  = 1/T.
Означення. Потік називають випадковим (casualstreamofrequests), якщо його події відбуваються у випадкові моменти часу.
Випадковий потік може бути описаний як випадковий вектор, що, як відомо, може бути заданий за законом розподілу двома способами:
- законом розподілу моментів появи подій
,                            (4.2)
де  випадкові моменти часу появи подій у потоці,
t1, t2, tn – їх призначення,
Р – ймовірність;
- багатовимірним законом розподілу системи випадкових величин Т1, Т2 ,…,Тn, що є довжинами інтервалів між послідовними подіями:
,                  (4.3)
де  zi – значення Ti, (i = 1,n).
У цьому випадку моменти настання подій можуть бути обчислені таким чином
t1 = t0 + z1
t2 = t1 + z2                                             (4.4)
………,
      tn = tn-1 + zn,
де t0 - момент початку потоку.

4.4.2 Найпростіший потік Пуассона

Під час розв’язання великого числа прикладних задач буває достатньо застосувати математичні моделі однорідних потоків, що задовольняють заявки стаціонарності, без післядії й ординарності.
Означення. Потік називається стаціонарним (stationarystreamofrequests), якщо ймовірність появи n подій на інтервалі часу (t, t+T) залежить від його розташування на часовій осі t.
Означення. Потік подій називається ординарним (ordinarystreamofrequests), якщо ймовірність  появи двох або більше подій протягом елементарного інтервалу часу є величина нескінченно мала у порівнянні з ймовірністю появи однієї події на цьому інтервалі, тобто  для  n = 2,3,…
Означення. Потік подій називається потоком без наслідків (Streamofrequestswithouttheconsequences), якщо для будь-яких інтервалів часу, що не перетинаються, число подій, що попадають на один з них, не залежить від числа подій, що попали на інший.
Означення. Якщо потік задовольняє стаціонарність, ординарність і без наслідків він називається найпростішим (simpleststreamofrequests) (потоком Пуассона).
Доведено, що для найпростішого потоку число n подій, що попадають на будь-який інтервал z розподілено за законом Пуассона
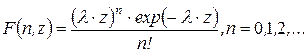              (4.5)
Ймовірність  того, що на інтервалі часу z не з'явиться жодної події дорівнює:
P(0, z) = ;  P(T < z) = 1 - .             (4.6)
Тоді ймовірність протилежної події, де за визначенням P(T < z) = F(z) – це функція розподілу ймовірності Т. Звідси одержимо, що випадкова величина Т розподілена за показовим законом
,                                (4.7)
де l  називають щільністю потоку. Причому , а .
Властивості найпростішого потоку Пуассона
Відомі дві властивості найпростішого потоку, що можуть бути використані під час розв’язування практичних задач.
1. Нехай деяка величина a = l х. Відповідно до властивостей Пуассонівського розподілу при а ® ¥ вона прямує до нормального закону розподілу, і тому для обчислення Р{Х(а) £ n}, де Х(а) – випадкова величина, що розподілена за Пуассоном з математичним сподіванням а, можна скористатися такою наближеною рівністю
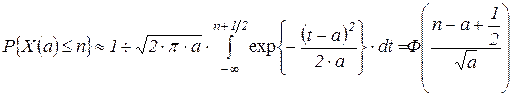,  (4.8)
де .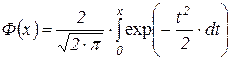
Ще одна властивість потоку Пуассона пов'язана з такою теоремою.
Теорема. Для показового розподілу інтервалу часу між заявками Т, незалежно від того скільки він тривав, частина часу, що залишилася, має той же закон розподілу.
Доведення. Нехай Т розподілено за показовим законом F(x) = 1 - . Припустимо, що проміжок часу а вже тривав якийсь час а < Т. Знайдемо умовний закон розподілу частини проміжку часу, що залишилася, Т1 = Т - а
Fa(x) = P(T - a < x½ T >x).                        (4.9)
Відповідно до теореми множення ймовірностей
P((T > a)(T – a <z)) = P(T > z) P(T – a < z |T > a) = P(T > a) Fa(z).         (4.10)
Звідси можна записати, що , однак подія  рівносильна події а < T < z + a, для якої
P(а < T < z + a) = F(z + a) – F(a).            (4.11)
З іншої сторони P(T > a) = 1 – F(a).
Таким чином, Fa(x) = (F(z + a) – F(a))/(1 – F(a)).
Звідси, з огляду на те, що  можна записати, що
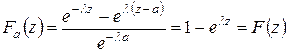.                 (4.12)
Цією властивістю характеризується тільки один вид потоків – найпростіші потоки Пуассона.
Зауваження. Дослідження задач ТСМО суттєво спрощується у припущенні, що вихідний потік є найпростішим потоком Пуассона. Однак критичне вивчення умов, що приводять до найпростішого потоку, змушують зробити висновок, що найпростіші потоки зустрічаються не так часто. Наприклад, найчастіше порушується ординарність (одночасно відбувається заявка одного і того ж номера телефону при цьому, необхідно ставити кілька машин під завантаження або розвантаження і т. д). Умова стаціонарності також часто порушується, наприклад, змінюється інтенсивність замовлень на переговори протягом доби. Недотримання умови без наслідків так само є звичайним, наприклад, поломка машин таксопарку, що може призвести (через збільшення навантаження) до поломок інших машин.
Однак у дійсності найпростіші потоки зустрічаються частіше, ніж це здається після наведених прикладів. Поясненням цього займався шведський учений Пальма. А пізніше Хінчін А. Я. довів одну загальну теорему, що є винятковою теоретичною цінністю. Він довів, що якщо потік є сумою великого числа n незалежних ординарних і стаціонарних потоків інтенсивністю lі , і жоден з них не порівнюється за потужністю з усім сумарним потоком, то за деяких аналітичних обмежень сумарний потік зводиться до найпростішого з інтенсивністю .
Теорема Хінчіна широко застосовується на практиці. Так під керівництвом Гнеденко було досліджено потік транспортних суден, що прибувають у порт. Статистичне оброблення дозволило зробити висновок про досить гарний збіг реального потоку з найпростішим. На підставі цього було зроблено прогнози щодо прибуття суден на наступні місяці.

4.4.3 Нестаціонарні потоки Пуассона

Теорема Хінчіна була узагальнена для потоків, що складаються з потоків неординарних і нестаціонарних. При цьому, якщо ці потоки незалежні і їх інтенсивність приблизно однакова, то сумарний потік близький до потоку Пуассона тільки із застосуванням параметра l (t). Причому l (t) називається миттєвою щільністю. Вона є границею відношення середнього числа подій, що приходяться на елементарний інтервал часу (t, t + x) до довжини інтервалу, коли останній прямує до нуля:
,                     (4.13)
де M(t) – математичне сподівання числа подій на інтервалі .
Доведено, що для такого потоку число подій n протягом часового інтервалу z, що починається в момент t0, розподілено за законом Пуассона
,                                 (4.14)
де m - математичне сподівання числа подій на інтервалі (t0, t + x)
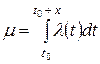.                                    (4.15)
Тут m очевидно залежить від довжини інтервалу і від його положення на часовій осі.
Аналогічно тому, як була виведена функція щільності розподілу ймовірності для найпростішого потоку Пуассона , можна отримати функцію щільності розподілу ймовірності Т для нестаціонарного потоку Пуассона
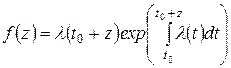.                            (4.16)
Розглянута модель належить математику Б. І. Григеліонісу. Цією моделлю описується велике число потоків – виклик лікаря до хворого, потік телеграм, потік замовлень на переговори, потоки пасажирів і т. д.

4.4.4 Потоки з обмеженим наслідком (потоки Пальма)

Іншим узагальненням найпростішого потоку є потік Пальма (Palmstream).
Означення. Потоком Пальма називається потік, що характеризується властивостями стаціонарності, ординарності і незалежності інтервалів часу Т між подіями.
Вимога незалежності інтервалів Т є слабкішою, ніж заявка без наслідку, а тому такі потоки називають потоками з обмеженими наслідками.
Теорема. Нехай у систему надходить потік заявок типу Пальма. Заявка, що застала усі канали зайнятими, одержує відмову. Якщо при цьому час обслуговування має показовий закон розподілу, то потік заявок, що не обслуговані, є потоком Пальма. У загальному випадку найпростіший потік є частковим випадком потоку Пальма. Його незалежні інтервали розподілені за показовим законом.
Ще одним прикладом потоків Пальма є потоки Ерланга, що можуть бути отримані таким чином.
Якщо з найпростішого потоку виключається кожна друга заявка, то потік, що залишився, утворить потік другого порядку, а якщо у потоці зберігається кожна третя заявка, то це - потік третього порядку і т. д. Для потоку k-го порядку функція щільності для інтервалу Т має такий вигляд
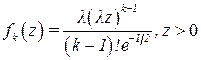.                         (4.17)
Із збільшенням порядку k функція fk(х) убуває, однак М[Т] зростає
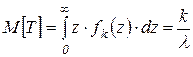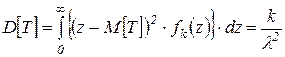;   .   (4.18)
Для достатньо великого k (практично для k = 5) потік Ерланга k-ого порядку можна вважати нормальним із зазначеними М[T] і D[T]. Це випливає з того, що інтервал часу Т між двома послідовними подіями у потоці Ерланга k-ого порядку є сумою k незалежних випадкових величин з одним законом розподілу. Тоді на підставі центральної граничної теореми теорії ймовірностей маємо доведення цього твердження.
Задаючи різні значення k у наведеному вище виразі можна отримати потоки, що характеризуються різними післядіями – від повної її відсутності (k = 1) до повного функціонального зв'язку між моментами появи подій (регулярний потік). І насправді для k = 1 отримуємо найпростіший потік, а для k = const і для k®¥ потік Ерланга наближається до регулярного. Властивості потоків Ерланга дають можливість широкого застосування цієї математичної моделі.

4.4.5 Потоки відновлення

На практиці часто приходиться стикатися з потоками, що отримали назву потоків відновлення. Прикладом такого потоку є ситуація, коли пристрій системи повинен знаходитися у стані безперервної роботи. Як тільки він перестає виконувати свої функції (старіння, поломка) його заміняють на новий. Моменти заміни tk, k = 1,2, … є випадковими, оскільки тривалість безвідмовної роботи кожного пристрою – є величина випадкова, незалежна і має свій розподіл F(z). Такі потоки позначають як GI – загальний вхідний потік (General Input).
Для потоків відновлення існує велике число різних задач, зокрема, задача визначення ймовірності  того, що протягом заданого проміжку часу T з'явиться k подій потоку. Простих формул, що були виведені для найпростішого потоку, тут уже немає.
Цікавими для практики є потоки, що із часом “рідшають”, проходячи через послідовність приладів обслуговування. Прикладом цього може бути деталь, що проходить ряд операцій і на кожній операції є ймовірність виявлення прихованого дефекту. У таких випадках деталь усувається, а первісний потік рідшає. Ще одним прикладом може служити послідовне у часі виправлення тексту декількома коректорами. При цьому кількість непомічених помилок, як очевидно, рідшає. Угорським математиком А. Реньї був отриманий цікавий результат, що полягає у такому. Потік відновлення піддається операції – кожна заявка залишається у потоці з ймовірністю q і викидається з потоку з ймовірністю p = 1 - q. Одночасно здійснюється зміна масштабу часу – за одиницю масштабу вважається проміжок довжиною q-1. Якщо це подвійне перетворення позначити символом Rq, то послідовне проведення перетворень Rq1 , Rq2 , …, Rqn еквівалентно одному перетворенню Rq1q2…qn ... . Теорема Реньї полягає у тому, що якщо тривалість безвідмовної роботи розподілена за законом F(х) має скінченне математичне очікування М і
                                      (4.19)
то послідовність потоків, що рідшають, прямує до найпростішого потоку Пуассона. Таким чином, у певних умовах потоки відновлення стають найпростішими, що ще раз підтверджує справедливість теореми Хінчіна.

4.5 Системи масового обслуговування з відмовами

4.5.1 Математичні моделі СМО з відмовами. Формули Ерланга

Для усталеного процесу обслуговування під час надходження у систему найпростішого потоку заявок з показниковим розподілом часу основні показники ефективності функціонування СМО з відмовами визначаються за такими формулами:
– середнє число заявок, що надходять у систему за середній час обслуговування
,                               (4.20)
де l  - щільність надходження заявок в одиницю часу,
tобс – середній час обслуговування однієї заявки одним каналом, хв/год,
m = 1/ tобс – інтенсивність обслуговування;
– ймовірність того, що обслуговуванням зайнято рівно k каналів.
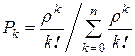,                                      (4.21)
де n - число каналів обслуговування;
– ймовірність того, що всі канали вільні від обслуговування
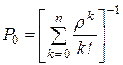;                               (4.22)
– ймовірність того, що заявку буде обслуговано (відносна пропускна здатність системи) ;
– ймовірність того, що всі заявки будуть обслуговані
;                         (4.23)
– абсолютна пропускна здатність системи ;
– середнє число каналів, зайнятих обслуговуванням
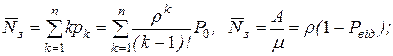      (4.24)
– середнє число каналів, вільних від обслуговування
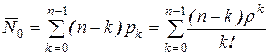;                    (4.25)
– коефіцієнт простою каналів ;
– коефіцієнт завантаження каналів .

4.5.2 Системи з послідовними каналами однієї продуктивності

У таких системах існує певна послідовність обслуговування заявок: канали другої, третьої та інших груп не розпочинають обслуговування доти, поки не будуть зайняті всі канали попередніх груп. Нехай існує і таких груп. Кількість каналів у кожній групі  Sj де 1£ j £ i.
Основною характеристикою функціонування системи є ймовірність відмови в обслуговуванні, ймовірність того, що заявка дістане відмову на каналах першої групи, тобто заявки надійдуть до каналів другої групи, визначиться з формули Ерланга
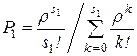.                                     (4.26)
Якщо всі канали першої групи зайняті, то заявки  надійдуть до обслуговування до другої групи. Ймовірність відмови каналами другої групи
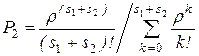.                         (4.27)
де s1, s2 - число каналів обслуговування в перший і другій групах. Якщо si позначити число каналів у i-й групі, то ймовірність проходження заявок через усю систему
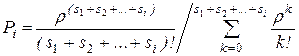.              (4.28)
Визначимо такі показники:
– ймовірність відмови в обслуговуванні на каналах j – іпослідовно розташованої групи
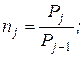                                        (4.29)
– ймовірність того, що канали j-ї послідовно розташованої групи обслуговують заявку, яка не обслуговувалась на каналах попередніх груп:
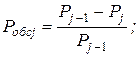                             (4.30)
– коефіцієнт продуктивності каналів j-ї послідовно розмі­щеної  групи
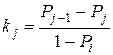;                                 (4.31)
– число заявок, які обслуговані N =AP,де N - число заявок, які обслуговані з ймовірністю обслуговування P, A - абсолютна пропускна здатність системи;
– число каналів обслуговування для того, щоб ймовірність втрачання хоча б однієї заявки була менша від заданої величини Pвід визначається із нерівності
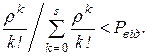                           (4.32)

4.5.3 Системи з послідовними каналами різної продуктивності

Розглянемо систему з двох каналів, які розміщені послідовно. Продуктивність першого з них характеризується параметром m1, а другого - m2.
Система працює таким чином. На перший канал надходить простіший потік заявок з інтенсивністю l. Заявки, які не були обслуговані першим каналом, у зв’язку з тим, що він був зайнятим, надходять для обслуговування на другий канал. Якщо він вільний, то заявка обслуговується, інакше, вона вважається загубленою для системи.
Основні формули для розрахунків.
1. Ймовірність того, що обидва канали вільні від обслуговування
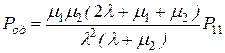.                    (4.33)
2. Ймовірність відмови в обслуговуванні заявок
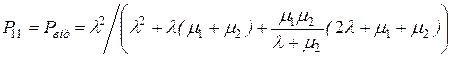.   (4.34)
3. Ймовірність того, що перший канал буде зайнятий обслуговуванням, а другий – вільним:
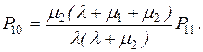                         (4.35)
4. Ймовірність того, що другий канал буде зайнятий обслуговуванням, а перший – вільним:
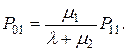                               (4.36)
5. Коефіцієнт завантаження першого каналу
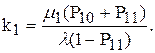                         (4.37)
Після підстановки значень P10 та P11 маємо
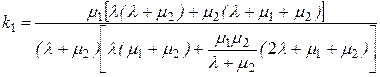.        (4.38)
6. Коефіцієнт завантаження другого каналу
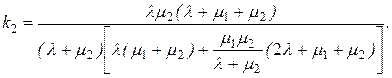      (4.39)
7. Коефіцієнт, який показує, в скільки разів перший канал пра­цює більше за другий:
                     (4.40)
Аналіз функціонування системи, яка складається з двох каналів обслуговування різної продуктивності, показує: щоб ефективність системи була найвищою, перший канал повинен мати вищу продуктив­ність.

4.5.4 Системи з нагромадженням заявок

При функціонуванні системи заявки надходять до нагромаджувача обсягом n з інтенсивністю l. Якщо заявка, яка надійшла, застає нагромаджувач заповненим, вона втрачається для системи. Через випадкові моменти часу до нагромаджувача звертається канал оброблення заявок і бере на обслуговування всі нагромаджені до того часу заявки. Час обслуговування цього масиву заявок випадковий з показниковим законом розподілу з параметром m . Як тільки весь масив заявок оброблено, канал знов звертається до збирача і т. ін. Основні показники функціонування системи визначимо за такими формулами.
1. Ймовірність того, що в нагромаджувач надійшло рівно k заявок
,  (k < n).                     (4.41)
2. Ймовірність відмови в обслуговуванні
.                         (4.42)
3. Середнє число заявок, що надійшли
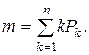                                    (4.43)
2. Коефіцієнт завантаження нагромаджувача
.                                        (4.44)
8. Середній час обслуговування однієї заявки
.                                  (4.45)
5. Обсяг нагромадження при заданій надійності обслуговування
                            (4.46)

4.5.5 Приклади оцінювання й аналізу ефективності СМО з відмовами

Задача 1. Телефонна станція має n = 6 міжміських ліній зв’язку. До послуг станції звертаються абоненти з заявками на проведення пере­говорів з інтенсивністю l = 30 заявок за годину. Середня тривалість однієї розмови tобс= 0,25 год. Визначити основні показники функціонування системи та умови, за яких вона здатна виконати поставлену задачу.
Результати розрахунків за формулами Ерланга запишемо у табл. 4.1.
Висновок. В організацію роботи телефонної станції слід внести зміни, які б привели до істотного поліпшення функціонування системи, оскільки ймовірність обслуговування має недостатнє значення.

Таблиця 4.1 - Результати розрахунків за формулами Ерланга

n

l

A

6

30

0,25

7,5

0,0015

0,6385

0,3615

19,155

2,7884

1,2116

0,796

Задача 2. Для перевірки радіоелементів розроблена станція, яка містить три послідовно розміщені стенди. Перший має s1 = 36 каналів для контролю, другий – s2 = 15, а третій – s3 = 5. Середнє число елементів, які надходять на станцію за 1 хвилину, l = 96, а середній час перевірки одного елементу одним каналом tобс = 1 хв. Нехай потік елементів підпорядковується пуассонівському, а час обслуговування - показниковому законам розподілу. Ймовірність контролю за одну перевірку Р = 0,9.
Оцінити ефективність функціонування станції контролю та стен­дів, які входять до неї.
Результати розрахунків зведено у табл. 4.2.

Таблиця 4.2 - Ефективність функціонування станції контролю та стендів, які входять до неї

Но-мер
п/п

Показник
ефективності

Для 1-го
стенда

Для 1-го та 2-го стендів

Для 1-го, 2-го та 3-го

1

0,6309

0,4796

0,4109

2

0,3691

0,5204

0,5801

3

0

0

0

4

38,434

49,958

58,69

5

38,429

49,958

58,681

6

0,5708

1,0422

1,3129

7

0,9841

0,9796

0,977

8

0,0159

0,0204

0,023

9

32

45

50

Висновок. З таблиці видно, що станція не може впоратися з контролем радіоелементів, оскільки перевіряється тільки до 50 елементів. Останні не контролюються, тобто необхідно станцію модернізувати.
Задача 3. Цех має контрольний стенд, обладнаний двома каналами, які зміщені послідовно. Канали перевіряють відповідність нормам основних параметрів виробів. Вироби надходять на стенд із щільністю l = 0,5 вироб/хв. Оскільки різні вироби мають різні відхилення від норми, то канали втрачають на перевірку в кожному випадку різний час. Середній час, необхідний для перевірки одного виробу першим каналом, tобс = 5 хв, а другим – tобс =  2,5 хв.
Оцінити ефективність роботи двох послідовно розташованих каналів.
Результати розрахунків зведено у табл. 4.3.

Таблиця 4.3 - Ефективність роботи двох послідовно розташованих каналів

0,5

0,2

0,4

0,36

0,2048

0,352

0,08

0,81

0,64

Таким чином, тільки 64 % усіх виробів буде перевірено. Якщо ж першим поставити канал з більшою продуктивністю tобс = 2,5 хв, то ймовірність перевірки буде Pобс = 0,65. Тобто, у цьому разі буде перевірено на 2%  виробів більше, ніж у першому варіанті.
Задача 4. Знайти орієнтовний обсяг буферної пам’яті ЕОМ, яка має середній час оброблення масиву інформації = 5 с. Потік повідомлень надходить зі щільністю l = 10 повідомлень за секунду. Можливість втрати повідомлення не має перевищувати 1%.
Обчислимо параметр  Після чого знаходимо, що , тобто буферна пам’ять ЕОМ повинна мати обсяг 232 повідомлення.

4.6 Оптимізація систем масового обслуговування з відмовами

Функціонування системи в оптимальному режимі можна визначити через основні показники ефективності, їх числові значення виражаються через n число каналів обслуговування, tобс - середній час обслуговування,
l - середнє число заявок, які надходять в систему за одиницю часу. Тому ймовірність обслуговування можна записати як
                                    (4.47)
Обернені залежності мають такий вигляд:
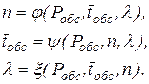                                    (4.48)
Функціонування СМО з відмовами в оптимальному режимі проаналізуємо порівнянням протилежних показників ефективності – ймовірності обслуговування й коефіцієнта завантаження каналів. При цьому припускаємо, що інші параметри системи набувають сталого значення.
Визначимо число каналів обслуговування, воно буде оптимальним, якщо ймовірність обслуговування і коефіцієнт завантаження каналів набувають однакових значень за умови, що n = const та
Тоді n = nопт, якщо Pобс=k3, при l = const, tобс = const. Оскільки , то й , звідки випливає, що .
Як відомо, середнє число каналів обслуговування  Тому остаточно маємо
                                 (4.49)
при
Для визначення оптимального середнього часу обслуговування запишемо
,                                 (4.50)
якщо  при .
Для оптимального числа заявок, якщо   при , можна записати, що
                               (4.51)
при
Таким чином, основними шляхами впливу на режим функціонування системи є вихідні дані задачі. А підвищення ймовірності обслуговування як основного по­казника ефективності функціонування системи можливе, по-перше, при сталих значеннях l та tобс і збільшенні числа каналів обслуговування, по-друге, при сталих значеннях n та l і скороченні середнього часу обслуговування за умови, що якість обслуговування не зменшуватиметься, і по-третє, при сталих значеннях n та tобс і зменшенні потоку заявок на обслуговування.

4.7 Системи масового обслуговування з очікуванням

4.7.1 Розімкнені СМО з очікуванням

Система обслуговування, складається з обмеженого числа каналів, кожний канал здатний водночас обслуговувати тільки одну заявку. Кожна заявка, що надійшла заново, яка застає всі канали зайнятими, стає в чергу і перебуває в ній доти, доки один з каналів не звільниться. Якщо ж заявка надходить в систему, коли є вільні канали, вона зразу обслуговується.
Нехай у систему надходить пуассонівський потік заявок із щільністю l із необмеженого за своєю спроможністю джерела. Час обслуговування однієї заявки tоьс є випадковою величиною, яка задовольняє показниковий закон розподілу з параметром m.
У стаціонарному режимі основні показники ефективності функціонування визначаються за формулами:
– ймовірність того, що всі канали вільні
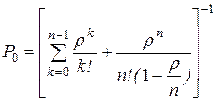, якщо            (4.52)

– ймовірність того, що у системі знаходиться k заявок
, якщо
, якщо                                       (4.53)
– ймовірність того, що всі канали зайняті обслуговуванням,
                                      (4.54)
– ймовірність того, що в черзі знаходиться рівно r заявок,
,                                     (4.55)
якщо
– середній час очікування обслуговування
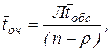                                         (4.56)
якщо
– середня довжина черги
;                            (4.57)
– середнє число заявок, які знаходяться в системі
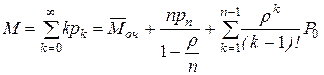;                   (4.58)
– середнє число вільних від обслуговування каналів
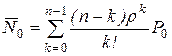;                               (4.59)
– коефіцієнт простою каналів
;                                    (4.60)
– середнє число зайнятих каналів
                                 (4.61)
– коефіцієнт завантаження каналів
;                                    (4.62)
– критерій вибору кращого варіанта системи обслуговування при її проектуванні
             (4.63)
де Gn – величина втрат за час tоч,,
qjx – вартість втрат, поєднаних з простоями заявок у черзі;
qnn – вартість одиниці часу простою каналу системи;
qn – вартість експлуатації каналу при обслуговуванні за одиницю часу.
Приклад розв’язання задач
У майстерні по ремонту радіоапаратури працює n = 5 майстрів. У середньому протягом робочого дня від населення надходить на ремонт
l = 10 апаратів. Загальна кількість апаратури, яка знаходиться у населення, досить значна. Апаратура виходить з ладу незалежно одна від одної. Тому можна вважати, що потік заявок пуассонівський. Кожен майстер протягом робочого дня може відремонтувати в середньому m = 2,5 радіоапаратури. Оцінити показники якості обслуговування майстерні.
Результати розрахунків зведено у табл. 4.4.

Таблиця 4.4 - Показники якості обслуговування майстерні

Л

4

0,013

0,554

7

2,8

1,55

11,1

18,15

0,96

4.7.2 Замкнені СМО з очікуванням

Система має n каналів обслуговування, кожний з них може водночас обслуговувати тільки одну заявку. У систему надходить простіший потік заявок з параметром l . Потік надходить із обмеженого джерела, так що в системі може знаходитися не більш як т заявок. Заявки, які надійшли в систему в момент, коли хоча б один канал був вільний, відразу ж йдуть на обслуговування. В протилежному випадку вони стають у чергу і очікують доки один з каналів не звільниться.
Наведемо остаточні результати для стаціонарного режиму.
1. Ймовірність того, що всі канали вільні від обслуговування
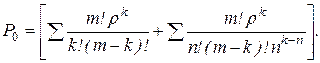                  (4.64)
2. Ймовірність того, що в системі знаходиться k заявок, з яких  k-n очікують обслуговування
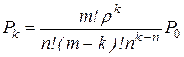                          (4.65)
при
3. Середнє число заявок, які очікують початку обслуговування
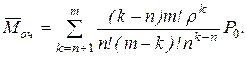              (4.66)
4. Коефіцієнт простою заявки
.                                       (4.67)
5. Середнє число заявок, які знаходяться в системі обслуговування
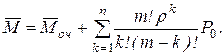                            (4.68)
6. Середнє число каналів, які вільні від обслуговування
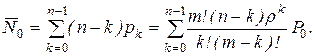                   (4.69)
7. Середній час перебування заявки у черзі
.                             (4.70)
8. Коефіцієнт простою каналів обслуговування
.                                              (4.71)
Приклад розв’язання задач
Два робітники обслуговують шість верстатів. Зупинки кожного працюючого верстата трапляються в середньому кожні півгодини. Процес налагодження займає у робітників в середньому 10 хвилин. Оцінити ефективність обслуговування верстатів.
Дані обчислення наведено у табл. 4.5.

Таблиця 4.5 - Ефективність обслуговування верстатів

0,33

0,156

0,137

0,073

1

0,62

0,31

1,9

Запитання і завдання для самоконтролю

1. У чому полягає задача масового обслуговування?
2. Які основні складові системи масового обслуговування?
3. Що є системою масового обслуговування з відмовами?
4. Наведіть два, три приклади СМО з відмовами.
5. Дайте постановку задачі аналізу СМО з відмовами.
6. Який вигляд має розмічений граф стану системи з відмовами?
7. Запишіть математичну модель СМО з відмовами.
8. Запишіть співвідношення для випадку стаціонарного режиму.
9. Які вихідні дані слід мати на увазі при оцінюванні СМО з відмовами?
10. Які основні показники ефективності функціонування системи треба знайти при розв'язуванні задачі?
11. Опишіть роботу системи з послідовно розташованими каналами однакової і різної продуктивності.
12. Доведіть, що для підвищення продуктивності обслуговування системи із двох каналів перший  повинен мати вищу продук­тивність.
І3. Поясніть, як працює система із збирачем заявок.
14. Як знайти необхідний обсяг збирача заявок?
15. Сформулюйте задачі оптимізації в СМО з відмовами.
16. Як визначити критерій, за яким оцінюють ефективність СМО?
17. Як обчислити оптимальне число каналів обслуговування?
18. Як визначити оптимальний час обслуговування?
19. Як обчислити оптимальне число заявок?
20. Які існують шляхи поліпшення організації обслуговування?
21. Як використати функцію втрат при оптимізації СМО з відмовами?
22. Як описати розімкнену СМО з очікуванням:
- диференціальні рівняння для ймовірностей стану;
- формули для ймовірностей стану;
- ймовірність того, що всі канали обслуговування зайняті;
- середня довжина черги;
- ймовірність того, що у черзі знаходиться рівно r заявок;
- середнє число заявок у системі;
- середнє число вільних каналів;
- середня тривалість очікування в системі.
23. Як описати замкнену СМО з очікуванням:
- диференціальні рівняння для ймовірностей стану;
- формули для ймовірностей стану;
- ймовірність знаходження частини заявок на обслугову­ванні;
- середнє число заявок, які простоюють;
- середнє число каналів обслуговування, які простоюють?

Варіанти індивідуальних аудиторних і домашніх завдань
1. Для умов задачі 1 (п. 4.5.5) знайти число ліній зв’язку, яке слід мати на станції за умови, щоб жодне звернення не отримало відмови на переговори. Для цього припустити, що ймовірність відмови дуже мала Pвід  = 0,0057.
2. Для умов задачі 1 (п. 4.5.5) визначити, який середній час обслуговування tобс треба мати, щоб ймовірність обслуговування Pобс = 0,738.
3. Для умов задачі 1 (п. 4.5.5) знайти, яке середнє число звернень l можна задовольнити, щоб ймовірність відмови Pвід була 0,1.
4. Спроектувати АТС, щоб ймовірність відмови в обслуговуванні не перевищувала 0,01. АТС проектується згідно з умовами, що потік викликів має щільність l = 0,5 викликів за хвилину. Середня тривалість однієї розмови tобс = 2 хв.
5. В умові задачі 3 (п. 4.5.5) перший канал вийшов з ладу. Водночас із його заміною прийнято рішення підвищити процент перевірених виробів до 80%. Яку продуктивність повинен мати перший канал?
6. Треба визначити обсяг бункера n  та час оброблення tобр масиву деталей, щоб оброблялося не менше ніж 95 % деталей, що надійшли, при цьому вартість системи була б мінімальною. Щільність надходження деталей l = 1 деталь на хвилину. Відомо, що вартість системи залежить від обсягу бункера та продуктивності блока обробки. Вартість бункера Cбун  = 3n одиниць вартості, а вартість блока обробки Собр = 8/tобр  вартості.
7. На міжміську телефонну станцію в середньому за 1 хвилину  надходить дві заявки на розмови. Середня тривалість однієї розмови - 4 хвилини. Розрахувати, яке число ліній зв’язку має бути, щоб система працювала в оптимальному режимі.
8. На станцію контролю якості продукції надходять підсилювачі з щільністю  l = 3 одиниці/хвилину. Станція має 9 робочих місць. Обчислити оптимальний середній час перевірки одного підсилювача.
9. На складі готової продукції працює 6 чоловік. На склад надходять автомобілі з вантажем. Середній час, який витрачається одним працівником на розвантаження однієї машини, становить 0,5 год. Якщо всі працівники зайняті розвантаженням, то новий автомобіль надходить до другого складу. Скільки автомобілів треба надіслати на склад, яка ймовірність обслуговування та коефіцієнт завантаження працівників?
10. Готові електровимірювальні канали перевіряють на надійність роботи перед відправкою з підприємства на базу. Бригада складається з 6 осіб. Кожний з них може водночас перевіряти тільки один канал. Середній час перевірки одним робітником одного каналу 0,5 год. Се­редня щільність надходження каналів l = 20 каналів/годину.
Оцінити ефективність функціонування бригади та, при необхідності, внести зміни в організацію її роботи.
11. За умовою попередньго завдання (№10) визначити, який середній час перевірки каналів має бути, щоб ймовірність обслуговування була 0,81.
12. За умовою завдання №10 знайти необхідне число працівників в бригаді, щоб ймовірність обслуговування була 0,95.
13. За умовою завдання №10 визначити, яке число каналів може перевірити бригада, якщо ймовірність перевірки каналів Pобс = 0,98.
14. АЗС з n = 5 колонками обслуговує потік автомашин з інтенсивністю l  = 1 машина за хвилину. Середній час обслуговування однієї машини tобс = 4 хв. Оскільки в районі немає іншої АЗС, то черга машин може зростати практично необмежено. Знайти характеристики АЗС.
15. Морський порт має n = 5 причалів для розвантажування суден. У середньому протягом місяця до порту надходить 20 суден великого тоннажу. Час розвантаження суден - величина випадкова, але в середньому на розвантаження одного судна витрачається шість робочих днів. Оцінити роботу порту.
16. З умов завдання №15 розглянути можливість збільшення про-пускної здатності порту за рахунок збільшення кількості причалів (n = 6).
17. З умови завдання №15 розглянути можливість збільшення пропускної здатності порту за рахунок збільшення кількості причалів за умови, що простій судна qоч = 100 од. на добу, як місячний простій причалу qnn =1000 од., а вартість місячної експлуатації причалу qn = 1000 од.
18. Три робітники обслуговують 8 верстатів, в середньому кожні 0,5 год. один з працюючих верстатів зупиняється. Процес налагодження займає у робітника в середньому 12 хвилин. Визначити основні характеристики системи обслуговування.
19. Є n = 3 майстри по ремонту 10 зразків обчислювальної апаратури, яка розташована в різних підрозділах підприємства. Для виклику майстра та ремонту техніки в середньому потрібно 6 днів. Нехай щільність потоку  l = 1 апарат за місяць. Якщо заявка на ремонт надійшла, коли є вільні майстри, то вона одразу ж надходить у відпо­відний   підрозділ. Інакше, заявка стає у чергу й очікує ремонту. Оцінити ефективність роботи майстрів.