---

5. МОДЕЛЮВАННЯ В ІГРОВИХ СИТУАЦІЯХ

 

Як уже неодноразово відзначалося, системний аналіз неможливий без врахування взаємодій даної системи із зовнішнім середовищем. Раніше згадувалася необхідність враховувати стани природи– здебільшого випадкових, стохастичних впливів на систему. Звичайно ж, природа не заважає (але і не допомагає) процесам системи усвідомлено, негативно або, навпаки, заохочуючи.Тому врахування зовнішніх природних впливів можна розглядати як «гру з природою», але в цій грі природа – не супротивник і не опонент, у неї немає мети існування взагалі, а тим більше – мети протидії нашій системі.
Зовсім інакше виглядає справа при врахуванні взаємодій даної системи з іншими, аналогічними або близькими за цілями свого функціонування. Як відомо, таку взаємодію називають конкуренцією.
Особливий розділ науки – теорія ігор (gametheory)дозволяє хоча б частково вирішувати ускладнення, що виникають під час системного аналізу в умовах протидії. Цікаво відзначити, що одна з перших монографій з цих питань називалася «Теорія ігор і економічної поведінки» (автори – Нейман і Моргенштерн, 1953 р.) і послужила своєрідним каталізатором розвитку методів лінійного програмування і теорії статистичних рішень. Як простий приклад використання методів теорії ігор в економіці розглянемо таку задачу. Нехай ви маєте всього три варіанти стратегій в умовах конкуренції S1, S2 і S3, наприклад, випускати протягом місяця один з 3-ох видів продукції). При цьому ваш конкурент має всього два варіанти стратегій C1 і C2 (випускати один з 2 видів своєї продукції, що можуть дещо замінювати вашу продукцію). При цьому змінювати вид продукції протягом місяця не дозволено ні вам, ні вашому конкуренту.
Нехай і вам, і вашому конкуренту вірогідно відомі наслідки кожного з власних варіантів поводінки, що описуються табл. 5.1.

Таблиця 5.1 – Наслідки гри

Цифри у табл. 5.1 означають таке:
- ви несете збитки в 2000 гривень, а конкурент має ту ж суму прибутку, якщо ви прийняли стратегію S1, а конкурент застосував C1;
- ви маєте прибуток у 2000 гривень, а конкурент втрачає ту ж суму, якщо ви прийняли S1 проти C2;
- ви несете збитки в сумі 1000 гривень, а конкурент одержує такий прибуток, якщо ваш варіант S2 виявився проти його варіанта C1 , і т.д.
Передбачається, що обидві сторони мають професійну підготовку в області ТССА і діють розумно, дотримуючись правила – варіант поведінки приймають один раз на весь місяць, не знаючи звичайно, що вирішив виконувати в цьому ж місяці конкурент.
По суті справи, у чисто життєвому сенсі – це звичайна «азартна» гра, у якій існує кінцевий результат, мета гри – виграш.
Цієї мети домагається кожен гравець, але не кожний може її домогтися. Варіанти поведінки гравців можна вважати ходами, а деяку множину ходів – розглядати як партію.
Нехай партія складається всього лише з одного ходу від кожної сторони. Спробуємо знайти цей найкращий хід спочатку для вашого конкурента – порозмірковуємо за нього.
Оскільки таблиця відома як вам, так і конкуренту, то його міркування можна промоделювати.
Вашому конкуренту варіант C2 явно невигідний – при будь-якому вашому ході ви будете у виграші, а конкурент у програші. Отже, з боку вашого супротивника буде, мабудь, прийнято варіант C1, що дає йому мінімум втрат.
Тепер можна порозмірковувати за себе. Начебто варіант S2 принесе нам максимальний виграш у 3000 гривень, але це за умови вибору стратегії C2 вашим конкурентом, а він мабуть, вибере C1.

Значить найкраще, що ми можемо зробити – вибрати варіант S3, розраховуючи на найменший з можливих виграшів – у 1000 гривень.

5.1 Класифікація ігрових ситуацій

Ігри, у загальному випадку, можна класифікувати за кількома критеріями, наприклад, такими як:
- кількість гравців;
- кількість стратегій;
- характер взаємодії гравців;
- характер виграшу;
- кількість ходів тощо.
Залежно від кількості гравців розрізняють ігри двох і n гравців. Перші з них найбільш вивчені. Ігри трьох і більш гравців менш досліджені через виникаючі при цьому принципові труднощі і технічні можливості отримання рішень, тобто, чим більше гравців – тим більше проблем.
За кількістю стратегій ігри поділяються на скінченні і нескінченні. Якщо у грі всі гравці мають скінченне число можливих стратегій, то вона називається скінченною(eventualgame). Якщо ж хоча б один з гравців має нескінченну кількість можливих стратегій гра називається нескінченною(endlessgame).
За характером взаємодії ігри поділяються на безкоаліційні (coalitionlessgame), де гравці не мають права вступати в угоди, утворювати коаліції і на коаліційні (кооперативні) (coalitiongame), де гравці можуть вступати в коаліції (у кооперативних іграх коаліції наперед визначені).
За характером виграшів ігри поділяються на ігри з нульовою сумою (gamewithazeroingsum) (загальний виграш усіх гравців не змінюється, а ділиться між гравцями, при цьому сума усіх виграшів дорівнює нулю) і на ігри з ненульовою сумою.
За видом функцій виграшу ігри поділяються на матричні, біматричні, безперервні, опуклі, сепарабельні, типу дуелей та ін.
Матрична гра (matrixgame) – це скінченна гра двох гравців з нульовою сумою, у якій задається виграш гравця 1 у вигляді матриці (рядок матриці відповідає номеру застосовуваної стратегії гравця 2; стовпець – номеру застосовуваної стратегії гравця 2; на перетині рядка і стовпця матриці знаходиться виграш гравця 1, що відповідає застосовуваним стратегіям). Для матричних ігор доведено, що кожна з них має розв’язок, що може бути знайдений шляхом зведення гри до задачі лінійного програмування.
Біматрична гра – це cкінченна гра двох гравців з ненульовою сумою, у якій виграші кожного гравця задаються матрицями окремо для відповідного гравця (рядок кожної матриці відповідає стратегії гравця 1, стовпець – стратегії гравця 2, а на їх перетині в першій матриці знаходиться виграш гравця 1, у другій матриці – виграш гравця 2.) Для таких ігор також розроблена відповідна теорія, однак розв’язувати їх значно складніше.
Безперервною (continuous game) вважається гра, де функція виграшів кожного гравця є безперервною залежно від застосовуваних стратегій. При цьому доведено, що ігри цього класу мають розв’язок, однак не розроблено практично прийнятних методів їх застосування.
Ігри, у яких функція виграшів опукла, називаються опуклими(protuberantgame). Для них розроблено прийнятні методи моделювання (пошук чистої оптимальної стратегії (визначеного числа) для одного гравця й імовірностей застосування чистих оптимальних стратегій іншого). Такі задачі моделюються порівняно легко.

5.2 Моделювання ігрових ситуацій у чистих стратегіях

Матрична гра двох гравців з нульовою сумою може розглядатися як така абстрактна гра двох гравців. Перший гравець має  m  стратегій  i = 1,2...m, другий має  n  стратегій  j = 1,2,...,n. Кожній парі стратегій  (i,j)  поставлено у відповідність число аij, що має сенс виграшу гравця 1 за рахунок гравця 2, якщо перший гравець прийме свою стратегію i, а 2 – свою стратегію j.
Кожен з гравців робить один хід: гравець 1 вибирає свою стратегію i (i =  ), гравець 2 – свою стратегію j (j =  ), після чого гравець 1 отримує виграш аij за рахунок гравця 2 (якщо аij < 0, то це значить, що гравець 1 платить другому суму програшу | аij | ). На цьому гра закінчується.
Кожна стратегія гравця  i= і  j =  часто називається чистою стратегією. Якщо розглянути платіжну матрицю
А = 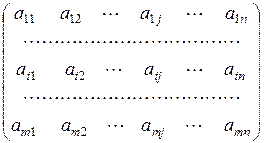,               (5.1)
то проведення кожної партії матричної гри з матрицею А  зводиться до вибору гравцем 1 i-го рядка, а гравцем 2 j-го стовпця і отримання гравцем 1 (за рахунок гравця 2) виграшу  аij.
Головним у дослідженні ігор є поняття оптимальних стратегій гравців. У це поняття інтуїтивно вкладається такий зміст – стратегія гравця є оптимальною, якщо застосування цієї стратегії забезпечує йому найбільший гарантований виграш за будь-яких стратегій іншого гравця.
Виходячи з цих позицій, гравець 1 досліджує матрицю виграшів А таким чином: для кожного значення i (i = ) визначається мінімальне значення виграшу залежно від застосовуваних стратегій гравця 2
аij ,  (i = ),                                   (5.2)
тобто визначається мінімальний виграш для гравця 1 за умови, що він прийме свою чисту стратегію i, потім з них відшукується така стратегія  i = iо, за якою цей мінімальний виграш буде максимальним, тобто знаходиться
аij = = .                          (5.3)
Означення 5.1. Число  за виразом (5.3) називається нижньою чистою ціною гри і показує, який мінімальний виграш може гарантувати собі перший гравець, застосовуючи свої чисті стратегії для будь-яких дій другого гравця.
Гравець 2 при оптимальній своїй поведінці повинен намагатись, по можливості, за рахунок своїх стратегій максимально зменшити виграш гравця 1. Тому для гравця 2 відшукується
аij ,                                         (5.4)
тобто визначається максимальний виграш гравця 1, за умови, що гравець 2 застосує свою j-ту чисту стратегію. Потім гравець 2 шукає таку j = j1 стратегію, за якою гравець 1 отримує мінімальний виграш, тобто знаходить
aij = = .                           (5.5)
Означення 5.2 Число , визначене за виразом (5.5), називається чистою верхньою ціною гри і показує, який максимальний виграш за рахунок своїх стратегій може собі гарантувати гравець 1. Іншими словами, застосовуючи свої чисті стратегії гравець 1 може забезпечити собі виграш не менше , а гравець 2 за рахунок застосування своїх чистих стратегій може не допустити виграш гравця 1 більше, ніж .
Означення 5.3. Якщо у грі з матрицею А  = , то говорять, що ця гра має сідлову точку (pointofsaddle) в чистих стратегіях і чистій ціні гри u = = .
Сідлова точка – це пари чистих стратегій  (iо, jо)  відповідно до гравців 1 і 2, за якими досягається рівність  = . У це поняття вкладено такий зміст: якщо один із гравців дотримується стратегії, що відповідає сідловій точці, то інший гравець не зможе діяти краще, ніж дотримуватись стратегії, що відповідає сідловій точці. Математично це можна записати й інакше:
,                                   (5.6)
де i, j – будь-які чисті стратегії відповідно до гравців 1 і 2;
(iо, jо) – стратегії, що утворюють сідлову точку.
Таким чином, виходячи з (5.6), сідловий елемент   є мінімальним в i-ому рядку і максимальним у j-ому стовпці матриці А. Відшукання сідлової точки матриці А здійснюється таким чином. У матриці А послідовно в кожному рядку знаходять елемент з мінімальним його значенням і перевіряють, чи буде цей елемент максимальним у своєму ж стовпці. Якщо це так, то цей елемент і буде  сідловим, а пари стратегій, що йому відповідають, утворюють сідлову точку.
Пари таких чистих стратегій (iо, jо) гравців 1 і 2, що утворюють сідлову точку і сідловий елемент  , називаються розв’язком гри. При цьому  iо і jо називаються оптимальними чистими стратегіями відповідно до першого і другого гравців.
Приклад 5.1

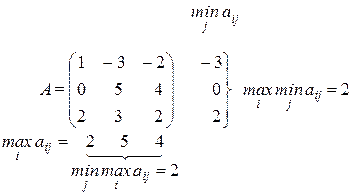
У наведеному прикладі сідловою точкою є пара  (iо = 3; jо = 1), задля якої u =  =  = 2. При цьому відзначимо, що хоча виграш у ситуації (3; 3) також дорівнює  2 =  = , відповідна їй клітинка матриці не буде сідловою точкою, оскільки цей виграш не є максимальним серед виграшів третього стовпця.
Приклад 5.2

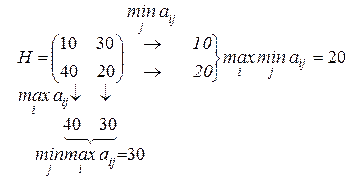
З аналізу наведеної платіжної матриці Н видно, що , тобто дана матриця не має сідлової точки. Якщо перший гравець вибирає свою чисту максимінну стратегію i = 2, то другий гравець, вибравши свою мінімаксну стратегію j = 2, програє тільки 20. У цьому випадку першому гравцю вигідно обрати стратегію  і = 1, тобто відхилитися від своєї чистої максмінної стратегії і виграти 30. Тоді гравцеві 2 буде вигідно обрати стратегію  j = 1, тобто відхилитися від своєї чистої мінімаксної стратегії і програти 10. У свою чергу гравець 1 повинен обрати свою 2-у стратегію, щоб виграти 40, а гравець 2 відповість вибором 2-ї стратегії і т.д.
Якщо для і-ї та к-ї стратегій першого гравця виконується умова  то існує таке j, для якого aij > akj, то стратегія і домінує над стратегією k. Остання може бути виключена з аналізу платіжної матриці гри.
Для другого гравця, якщо стратегія j домінує над стратегією l, та aij ³ ail , то існує таке i, для якого aij > ail, стратегію j другого гравця можна вилучити при відшуканні розв’язку гри.
Можна довести, що неефективним чистим стратегіям першого гравця відповідають ті рядки платіжної матриці, які домінуються деякою опуклою лінійною комбінацією інших рядків цієї матриці, а неефективним чистим стратегіям другого гравця відповідають ті стовпці платіжної матриці, які домінують над деякою опуклою лінійною комбінацією інших стовпців цієї матриці. Отже, встановивши факти домінування, відповідні чисті стратегії гравців можна відкинути, викресливши з матриці їх стовпці та рядки. Таким чином, вдається спростити гру, особливо якщо факт домінування очевидний.
Приклад 5.3. Знайти неефективні чисті стратегії у наведеній нижче грі і спростити відповідну платіжну матрицю
.
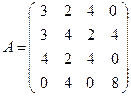Оскільки третій рядок матриці домінує над першим, то викресливши з матриці перший рядок, маємо
.
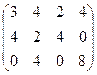У новій матриці третій стовпець домінує над першим. Тому, викресливши перший стовпець, отримаємо
.
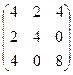В отриманій матриці перший стовпець домінує над опуклою лінійною комбінацією другого та третього стовпців, оскільки

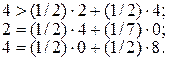
Викресливши перший стовпець, маємо .
У свою чергу, в цій матриці опукла лінійна комбінація другого й третього рядків домінує над першим рядком, оскільки

Викреслимо перший рядок і отримаємо матрицю . При цьому можна показати, що ціна гри з платіжною матрицею А' дорівнює ціні вихідної гри з платіжною матрицею А, а оптимальні стратегії гравців можна отримати, розв’язавши гру з матрицею А'.

5.3 Моделювання ігрових ситуацій у змішаних стратегіях

Дослідження в матричних іграх починається з пошуку її сідлової точки в чистих стратегіях. Якщо матрична гра має сідлову точку в чистих стратегіях, то пошуком цієї сідлової точки і закінчується дослідження гри. Якщо ж у грі немає сідлової точки в чистих стратегіях, то можна знайти нижні і верхню чисті ціни цієї гри, які вказують, що гравець 1 не повинен сподіватися на виграш більший, ніж верхня ціна гри, і може бути упевнений в отриманні виграшу не менше нижньої ціни гри. Покращення рішень матричних ігор слід шукати у використанні таємності застосування чистих стратегій і можливості багаторазового повторення ігор у вигляді партії.
Цей результат досягається шляхом застосування чистих стратегій випадково, з визначеною імовірністю.
Означення 5.4. Змішаною стратегією гравця (mixedplayerstrategy) називається повний набір ймовірностей застосування його чистих стратегій, тобто – це вектор, компонентами якого є ймовірності вибору чистих стратегій гравців.
Таким чином, якщо гравець 1 має  m  чистих стратегій  1,2,...,m, то його змішана стратегія  x – це набір чисел  x = (x1, ..., xm), що задовольняють співвідношення xi ³ 0,  (i = 1,m),  = 1.
Аналогічно для гравця 2, що має n чистих стратегій, змішана стратегія  y – це набір чисел y = (y1, ..., yn),  yj ³ 0,  (j = 1,n),  = 1.
Оскільки застосування гравцем щораз тільки однієї чистої стратегії виключає застосування іншої, то чисті стратегії є неспільними подіями. Крім того, вони є єдиними можливими подіями.
Чиста стратегія – це окремий випадок змішаної стратегії. Дійсно, якщо в змішаній стратегії яка-небудь i-та  чиста стратегія застосовується з ймовірністю 1, то всі інші чисті стратегії не застосовуються. І ця  i-та  чиста стратегія є частковим випадком змішаної стратегії. Для дотримання таємності кожен гравець застосовує свої стратегії незалежно від вибору іншого гравця.
Означення 5.5. Середній виграш гравця 1 у матричній грі з матрицею А описується у вигляді математичного очікування його виграшів
E (A, x, y) = = x A y.                       (5.7)
Перший гравець має на меті за рахунок зміни своїх змішаних стратегій х максимально збільшити свій середній виграш Е (А, х, y), а другий – за рахунок своїх змішаних стратегій намагається зробити Е (А, х, y) мінімальним, тобто для розв’язання гри необхідно знайти такі  х  і  y, при яких досягається верхня ціна гри
 Е (А, х, y).                                      (5.8)
Аналогічною повинна бути ситуація і для гравця 2, тобто нижня ціна гри повинна бути
 Е (А, х, y).                                      (5.9)
Подібно іграм, що мають сідлові точки  в чистих стратегіях, вводиться таке означення: оптимальними змішаними стратегіями  гравців 1 і 2 називаються такі набори  хо і  уо , згідно з якими задовольняються рівності
 Е (А, х, y) =  Е (А, х, y) = Е (А, хо, уо).    (5.10)
Величина Е (А, хо ,уо) при цьому називається ціною гри і позначається через  символ u.
Є також й інше означення оптимальних змішаних стратегій:  хо, уо називаються оптимальними змішаними стратегіями відповідно до гравців 1 і 2, якщо вони утворять сідлову точку:
Е (А, х, уо)£ Е (А, хо, уо)£ Е (А, хо, у).             (5.11)
Оптимальні змішані стратегії і ціна гри називаються розв’язком матричної гри.
Основна теорема матричних ігор має вигляд:
Теорема (про мінімакс). Для матричної гри з будь-якою матрицею А існують рівні між собою величини  Е(А, х, y) і
 Е (А, х, y).
Звідси, для того щоб x* = (x*1,…, x*m)була оптимальною змішаною стратегією першого гравця для матричної гри з нульовою сумою, платіжною матрицею А та ціною гри n , необхідно та достатньо виконання нерівностей
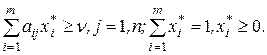                   (5.12)
Для другого гравця у* = (у*1,…, y*n) буде оптимальною змішаною стратегією, якщо
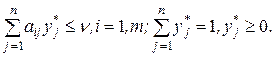               (5.13)
Компонентами векторів (х*, у*)є ймовірності вибору чистих стратегій гравцями в змішаній стратегії.

5.4 Властивості математичних моделей ігрових ситуацій

Позначимо через G (Х,Y,А) гру двох осіб з нульовою сумою, у якій гравець 1 вибирає стратегію  х Î Х , гравець 2 –  y ÎU, після чого гравець 1 отримує виграш А = А (х, y) за рахунок  гравця 2.
Означення 5.6. Стратегія х1 гравця 1 домінує (суворо домінує) над стратегією  х2, якщо А (х1, y)³ А (х2, y)(А (х1, y) > А (х2, y)),   y ÎU.
Стратегія y1 гравця 2 домінує (суворо домінує) над стратегією y2, якщо А (х, y1)£ А (х, y2)(А (х, y1) < А (х, y2)), х Î Х.
При цьому стратегії х2 і y2 називаються домінованими (суворо).
Спектром змішаної стратегії (mixedplayerstrategy spectrum) гравця у скінченній антагоністичній грі називається множина усіх його чистих стратегій, ймовірність яких відповідно до цієї стратегії позитивна.
Властивість 5.1. Якщо чиста стратегія одного з гравців знаходиться в спектрі деякої його оптимальної стратегії, то виграш цього гравця в ситуації, утвореній даною чистою стратегією і будь-якою оптимальною стратегією іншого гравця, дорівнює значенню скінченної антагоністичної гри.
Властивість 5.2.Жодна суворо домінована чиста стратегія гравця не знаходиться в спектрі його оптимальної стратегії.
Гра G¢ = (Х¢,Y¢,А¢) називається підгрою гри G (Х, Y, А), якщо Х¢Ì Х, U¢ÌU, а матриця А¢ є підматрицею матриці А. Матриця А¢ при цьому будується такий чином. В матриці А залишаються рядки і стовпці, що відповідають стратегіям Х¢ і U¢, а інші “викреслюються”. Усі ті, що залишаться після цього в матриці А і будуть утворювати матрицю А¢.
Властивість 5.3. Нехай G = (Х,Y,А) – скінченна антагоністична гра, а G¢= (Х \ х¢,Y,А) – підгра гри G, а х¢ – чиста стратегія гравця 1 у грі G, що домінується деякою стратегією , і спектр якої не містить х¢. Тоді будь-який розв’язок (хо, yо, u) гри G¢ є розв’язком гри G.
Властивість 5.4. Нехай G = (Х,Y,А) – скінченна антагоністична гра, а G¢= (Х,Y \ y¢,А) – підгра гри G, а y¢– чиста стратегія гравця 2 у грі G, що домінується деякою стратегією , і спектр якої не містить y¢. Тоді будь-який розв’язок гри G¢є розв’язком G.
Властивість 5.5. Якщо для чистої стратегії х¢ гравця 1 виконуються умови властивості 5.3, а для чистої стратегії y¢ гравця 2 виконуються умови властивості 5.4, то будь-який розв’язок гри G¢ = (Х \ х¢,Y \ y¢,А) є розв’язком гри G = (Х,Y,А).
Властивість 5.6. Трійка (хо, yо, u) є розв’язком гри G = (Х,Y,А) тоді і тільки тоді, коли (хо, yо, ku +а) є розв’язком гри G(Х,Y,кА+а), де а – будь-яке дійсне число, k > 0.
Властивість 5.7. Для того, щоб  хо = () була оптимальною змішаною стратегією матричної гри з матрицею А і ціною гри u, необхідно і достатньо виконання таких нерівностей:
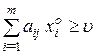,       (j = ).                      (5.14)
Для того, щоб  yо = ( , ..., , ..., ) була оптимальною змішаною стратегією гравця 2 необхідно і достатньо виконання нерівностей:
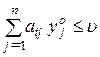,    (i = ).                        (5.15)
З останньої властивості випливає: щоб встановити, чи є передбачувані (х, y) і u розв’язком матричної гри, досить перевірити, чи задовольняють вони нерівності (5.14) і (5.15). З іншого боку, знайшовши ненегативні розв’язки нерівностей (5.14) і (5.15) спільно з рівняннями
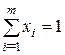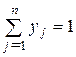,                                  (5.16)
отримаємо розв’язок матричної гри.
Таким чином, розв’язок матричної гри зводиться до пошуку ненегативних параметрів розв’язань лінійних нерівностей (5.14) (5.15) і лінійних рівнянь (5.16). Однак, це вимагає великого обсягу обчислень, який зростає зі збільшенням числа чистих стратегій гравців.
Наприклад, для матриці  33  маємо систему з 6 нерівностей і 2 рівнянь. Тому, по-перше, слід, використовуючи властивості 5.2 і 5.3, зменшити, по можливості, число чистих стратегій. А, по-друге, в усіх випадках перевірити виконання рівності
 = .                       (5.17)
Якщо ця рівність виконується, то обидва гравці мають чисті оптимальні стратегії (гравець 1 - чисту максимінну, а гравець 2 - чисту мінімаксну). Інакше, хоча б в одного гравця оптимальні стратегії будуть змішаними. Для ігор невеликої розмірності ці розв’язки знаходять, застосовуючи властивості  5.1 – 5.5.
Зауваження. Слід відзначити, що виключення не строго домінованих стратегій може призвести до втрати деяких розв’язків. Якщо ж виключаються тільки строго доміновані стратегії, то множина розв’язків гри не зміниться.
Приклад 5.4. Нехай G = (Х,Y,А), де Х = {1, 2, 3, 4}; Y = {1, 2, 3, 4}, а функція виграшу А задана таким чином:

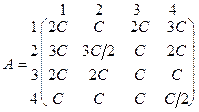
де C > 0.
Розв’язання. Насамперед відзначимо, що за властивістю 5.6 досить розв’язати гру G1 = (Х,Y,А), де А1 = А1/C . У матричній формі гра G1 визначається матрицею виграшів
.
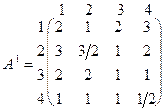Елементи четвертого рядка цієї матриці  “ £ ”  відповідних елементів третього рядка, а тому третя стратегія гравця 1 домінує над четвертою. Крім того, елементи першого стовпця матриці  А1  “ ³ ” відповідних елементів другого стовпця. Отже, друга стратегія гравця 2 домінує над його першою стратегією.
Далі із властивості 5.5 випливає, що будь-який розв’язок гри G2 = (Х \ {4}, Y \ {1}, А1) є розв’язком гри G1. У матричній формі гру G2 можна описати матрицею
.
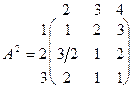Очевидно, що елементи другого рядка  “ ³”  півсуми відповідних елементів першого і третього рядків. Крім того, елементи третього стовпця матриці  А2  “ ³“  відповідних елементів другого стовпця.
Застосовуючи властивість 5.5 одержимо, що будь-який розв’язок гри G3 = (Х \ {4,2}, Y \ {1,4}, А2), тобто

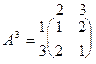
є розв’язком гри G2, а отже і гри G1.
Матриця А3 не має сідлової точки, тому що не виконується рівність (5.17), і, значить, гра G3 не має розв’язку в чистих стратегіях, тобто оптимальні стратегії гравців є змішаними. Ці стратегії, у даному випадку, легко знайти з аналізу структури матриці А3. Оскільки матриця А3 симетрична, можна припустити, що гравці в оптимальній стратегії використовують свої чисті стратегії з рівними ймовірностями.
Дійсно, якщо гравець 1 вибирає з рівними ймовірностями стратегії 1 і 3, то під час застосування кожної з двох чистих стратегій гравцем 2 математичне сподівання виграшу гравця 1 буде рівним
   або   .
Аналогічно, якщо гравець 2 використовує свої чисті стратегії 2 і 3 з рівними ймовірностями, то математичне сподівання його програшу буде дорівнювати 3/2. Отже, зазначені стратегії є оптимальними в грі G3, а величини 3/2 – значенням гри G3. З попереднього випливає, що ці стратегії оптимальні також і у грі G1.
Таким чином, стратегія Х = (1/2 , 0, 1/2, 0) є оптимальною стратегією гравця 1, стратегія Y = (0, 1/2, 1/2, 0) – оптимальною стратегією гравця 2 у грі G1, а значення гри G1 дорівнює 3/2. У силу властивості 5.4 розв’язком гри G буде трійка  (Х, Y, 3С/2 ).

5.5 Алгебраїчний метод моделювання ігрових ситуацій

Нехай задана матрична гра порядку 2 ´ 2, що описується матрицею
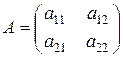.                                               (5.18)
Насамперед необхідно перевірити, чи є в даній ігровій ситуації сідлова точка. Якщо це так, то гра має розв’язок в чистих стратегіях, причому оптимальними стратегіями гравців 1 і 2 відповідно будуть чиста максимінна і чиста мінімаксна стратегії.
Якщо ж гра не має чистих стратегій, то обидва гравці мають тільки такі оптимальні стратегії, що використовують усі свої чисті стратегії з позитивними ймовірностями.
Інакше один із гравців (наприклад 1) має чисту оптимальну стратегію, а інший – тільки змішані. Не обмежуючи загальності, можна вважати, що оптимальною стратегією гравця 1 є вибір з ймовірністю 1 першого рядка. Далі з властивості 5.1 випливає, що а11 = а12 = u  і матриця має вигляд
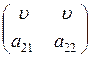.                                  (5.19)
Звідси легко побачити, що для матриць такого виду одна із стратегій гравця 2 є така, що домінує. Отже, за властивістю 5.4 цей гравець має чисту стратегію, що суперечить припущенню.
Нехай Х = (x, 1 -x) – змішана оптимальна стратегія гравця 1. Оскільки гравець 2 має змішану оптимальну стратегію, з властивості 5.1 отримаємо, що (див. також властивість 5.7)
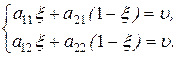                                     (5.20)
Звідси випливає, що при u ¹ 0 стовпці матриці А не можуть бути пропорційними з коефіцієнтом, відмінним від одиниці. Якщо ж коефіцієнт пропорційності дорівнює одиниці, то матриця А приймає вид
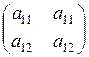                                             (5.21)
і гравець 1 має чисту оптимальну стратегію (він вибирає з ймовірністю 1 той з рядків, елементи якого не менші відповідних елементів іншого), що суперечить припущенню. Отже, якщо u ¹ 0 і гравці мають тільки змішані оптимальні стратегії, то визначник матриці А відмінний від нуля. З цього випливає, що остання система рівнянь має єдиний розв’язок. Розв’язуючи цю систему, знаходимо
,                                    
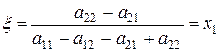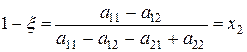,                      (5.22)
.                                          
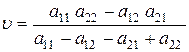Аналогічні міркування приводять нас до того, що змішана оптимальна стратегія  гравця  2 Y = (h, 1 - h)  задовольняє систему рівнянь
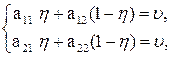                             (5.23)
звідки
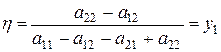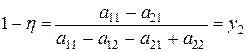; .       (5.24)
Якщо ж платіжна матриця має розмірність т ´ n, то для того, щоб знайти розв’язок такої гри, треба відшукати такі невід’ємні xi, i = 1…m,  yj, j = 1…n, які задовільняють співвідношення
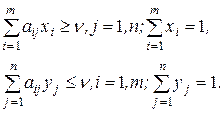                                     (5.25)
Замінимо всі нерівності на рівності й спробуємо розв’язати отриману систему рівнянь. Якщо всі xi  ³ 0, i = 1,…, m і yj ³  0, j = 1,…, n, то буде знайдено розв’язок гри. Інакше, якщо серед  xi чи yj є хоч один недодатний елемент, це означає, що заміна всіх нерівностей рівностями несправедлива і треба тільки частину нерівностей замінити рівностями і розв’язати ту саму систему. Перебираючи послідовно всі комбінації рівностей і нерівностей та розв'язуючи їх, відшукуємо розв’язок гри. При цьому слід мати на увазі, якщо для будь-якого i = 1,…, m буде виконуватись нерівність
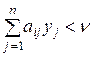,                                  (5.26)
то xi = 0.
Якщо ж для будь-якого j = 1,…, n буде
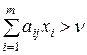,                                   (5.27)
то yj = 0.
Приклад 5.5. Розв’яжемо гру порядку 2 ´ 2, що описується матрицею
.
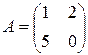Оскільки у цій грі матриця сідлової точки немає, тому шукаємо розв'язок у змішаних стратегіях. Ймовірності використання окремих чистих стратегій обчислюються за наведеними вище формулами:
         
        
при цьому ціна гри визначиться як
,
а змішані стратегії гравців мають вигляд X* = (5/6, 1/6), Y* = (1/3, 2/3).
Приклад 5.6. Розв’яжемо гру порядку 2 ´ 2, що описується матрицею
.
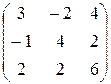Розглянемо випадок, коли всі нерівності замінено на рівності:
          
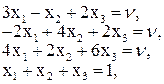
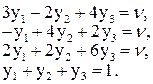
Ці рівняння не мають такого розв’язку, щоб ймовірності xi та yj були невід’ємні. Замінюючи рівності на нерівності, приходимо до такої системи:
         
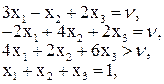
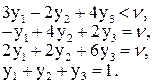
З нерівностей  і  випливає, що y3 = 0 x1 = 0.
Тепер вже розв’яжемо таку систему рівнянь:
         

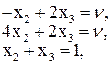
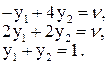
Вона має такий розв’язок: x2 = 0,  x3 = 1,  y1 = 2/5,  y2 = 3/5, n = 2. Таким чином, ціна гри дорівнює 2, оптимальна змішана стратегія першого гравця Х* = (0, 0, 1), другого Y* = (2/5,3/5,0 )

5.6 Графічний метод розв’язання ігор 2 ´ n і m ´ 2

Пояснимо метод на прикладах.
Приклад 5.7.Розглянемо гру, що задана платіжною матрицею

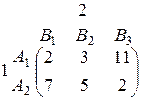
На площині  хОy  введемо систему координат і на осі Ох  відкладемо відрізок одиничної довжини А1, А2, кожній точці якого поставимо у відповідність деяку змішану стратегію гравця 1 (х, 1-х) (рис.5.1). Зокрема точці А1 (0;0) відповідає стратегія А1, а  А2 (1;0) – стратегія А2 і т. д.

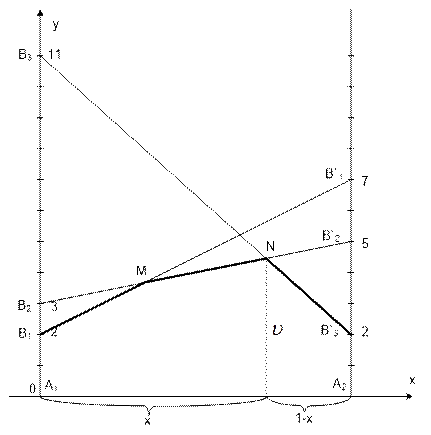
Рисунок 5.1 – Розв’язання приклада 5.7

У точках А1 і А2 відновимо перпендикуляри, на яких будемо відкладати виграші гравців. На першому перпендикулярі (у даному випадку він збігається з віссю 0y) відкладемо виграш гравця 1 при стратегії  А1, а на другому – при стратегії А2. Якщо гравець 1 застосує стратегію А1, то виграє при стратегії В1 гравця 2 – 2 у.о., при стратегії В2 – 3 у.о., а при стратегії В3 – 11у.о.. Числам 2, 3, 11 на осі 0х відповідають точки В1, В2 і В3. Якщо ж гравець 1 застосує стратегію А2, то його виграш при стратегії В1 дорівнює 7 у.о., при В2 – 5 у.о., а при В3 – 2 у.о.. Ці числа визначають точки В¢1, В2¢, В3¢ на перпендикулярі, відновленому в точці А2.
З'єднуючи між собою точки В1 і В¢1, В2 і В¢2, В3 і В¢3 отримаємо три прямі, відстань до яких від осі 0х визначає середній виграш при будь-якому поєднанні відповідних стратегій. Наприклад, відстань від будь-якої точки відрізка В1В¢1 до осі 0х визначає середній виграш u1 при будь-якому поєднанні стратегій А1 А2 (з частотами  х  і  1–х) і стратегією В1 гравця 2. Ця відстань дорівнює
2х1 + 6(1 - х2) = u1 .
(Згадаємо планіметрію і розглянемо трапецію А1 B1 B¢1 A2). Таким чином, ординати точок, що належать ламаній  В1 M N В¢3  визначають мінімальний виграш гравця 1 при застосуванні ним будь-яких змішаних стратегій. Ця мінімальна величина є максимальною в точці  N. Отже цій точці відповідає оптимальна стратегія Х* = (х, 1-х), а її ордината дорівнює ціні гри u. Координати точки N знаходимо як точку перетинання прямих В2 B¢2 і В3 B¢3. Відповідні два рівняння мають вид
.
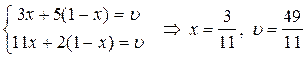Отже Х = (3/11; 9/11), при ціні гри  u = 49/11. Таким чином, ми можемо знайти оптимальну стратегію за допомогою матриці  .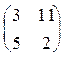
Оптимальні стратегії для гравця 2 можна знайти із системи

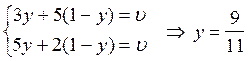
і, отже, Y = (0; 9/11; 2/11). (З рисунка видно, що стратегія B1 не ввійде в оптимальну стратегію.
Приклад 5.8. Розв’яжемо гру, задану матрицею
.
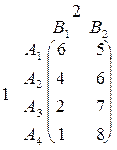Розв’язання. Матриця має розмірність 2 × 4. Будуємо прямі, що відповідають стратегіям гравця 1 (рис. 5.2). Ламана  А1 K А¢4  відповідає верхній границі виграшу гравця 1, а відрізок NK – ціні гри. Розв’язок гри при цьому такий
U = ( ; );     Х = ( ; 0; 0; );    u = .

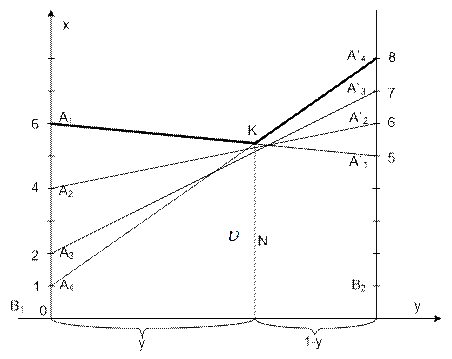
Рисунок 5.2 – Розв’язання прикладу 5.8

5.7 Матричний метод моделювання ігрових ситуацій

Нехай треба розв’язати гру з платіжною матрицею A = (aij)m´n і нехай В - будь-яка квадратна підматриця матриці А, поря­док якої r ³ 2. Тоді алгоритм матричного методу полягає у ви­конанні таких операцій.
І. Вибираємо квадратну підматрицю В матриці А і обчислюємо
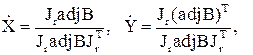                      (5.28)
де Jr = /1, 1, ..., 1/ - одиничний вектор-рядок;
adjB - матриця, приєднана до В;
(х)T- індекс транспонування (у даному випадку х = adjB);
 - вектор, побудований з Х  викреслюванням елементів, які відповідають рядкам, викресленим з А під час побудови В;
 – вектор, побудований із Y викреслюванням елементів, які відповідають стовпцям, викресленим з А під час побудови В.
2. Якщо деякі  xi < 0, i = 1,…, r або yj < 0 j = 1,…, r, то відкидаємо підматрицю В та спробуємо аналізувати другу.
3. Якщо всі xi  ³ 0, i  = 1,…, r  та yj ³ 0,  j = 1,…, r, то обчислюємо
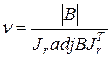.                                        (5.29)
4. Будуємо X з  та Y з , поширюючи ці вектори нулями на тих місцях, де ми викреслювали рядки чи стовпці під час побудови підматриці В.
5. Перевіряємо виконання співвідношень
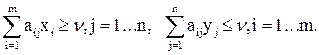                  (5.30)
Якщо хоча б одне з них не виконується, відкидаємо підматриці і спробуємо аналізувати другу.
Приклад 5.9. Розв’яжемо гру з платіжною матрицею

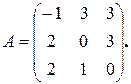
Оскільки матриця А  квадратна, то її можна розглядати як підматрицю В, порядок якої r = 3. Тоді

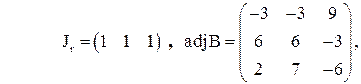
а розв’язок гри, обчислений за наведеними вище формулами, має вигляд

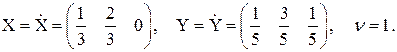
З дев'яти підматриць порядку r = 2 лише одна має додатковий розв’язок, а саме 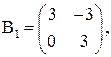для якої
 
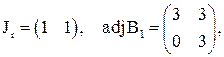
а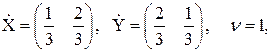
звідки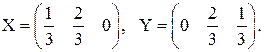
Як бачимо, перший гравець має єдину оптимальну стратегію, тоді як другий - множину оптимальних стратегій:
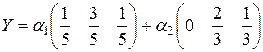, де
Виникає запитання, чи можна зробити вибір між різними оптималь­ними стратегіями. Нехай перший гравець вибрав змішану стратегію Х, а другий - чисту стратегію j. Тоді математичне сподівання виграшу першого гравця дорівнює E(X, j).

Змішана стратегія Х  домінує над змішаною стратегією Х¢, якщо для кожної чистої стратегії j  другого гравця  та існує хоча б одна така стратегія j, для якої  Е(Х, j) > Е(Х', j). У такому випадку стратегія Х називається найкращою, якщо вона оптимальна та жодна інша стратегія не домінує над нею. В розглянутому вище прикладі в другого гравця найкраща стратегія - це Y= (0, 2/3, 1/3).

5.8 Ітеративні методи моделювання ігрових ситуацій

Зведення матричних ігор до задач лінійного програмування. Припустимо, що ціна гри додатна (u > 0). Якщо це не так, то згідно з властивістю 5.6 завжди можна підібрати таке число с, додаток якого до всіх елементів матриці виграшів дає матрицю з додатними елементами, і отже, з додатними значеннями ціни гри. При цьому оптимальні змішані стратегії обох гравців не змінюються.
Отже, нехай дана матрична гра з матрицею А розмірністю m ´ n. Відповідно до властивості 5.7 оптимальні змішані стратегії х = (х1, ..., хm), y = (y1, ..., yn) щодо гравців 1 і 2 і ціна гри u повинні задовольняти співвідношення.
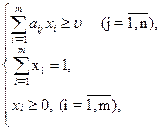                                        (5.31)
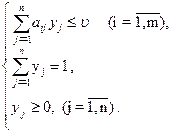                                               (5.32)
Розділимо всі рівняння і нерівності в (5.31) і (5.32) на u (це можна зробити, оскільки за припущенням u > 0) і введемо позначення :
     ,          .
Тоді (5.31) і (5.32) перепишеться у вигляді :
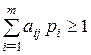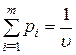,     ,     ,     ,               (5.33)
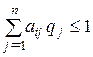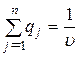,     ,     ,     .              (5.34)
Оскільки перший гравець намагається знайти такі значення хi і, отже, pi, щоб ціна гри u  була максимальною, розв’язок першої задачі зводиться до пошуку таких додатних значень  pi  , для яких
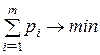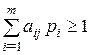,   .                             (5.35)
Оскільки другий гравець намагається знайти такі значення yj і, отже, qj, щоб ціна гри uбула найменшою, розв’язок другої задачі зводиться до пошуку таких додатних значень  qj,  , для яких
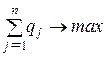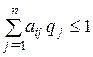,   .                                     (5.36)
Формули (5.35) і (5.36) описують двоїсті одна до одної задачі  лінійного програмування (ЛП). Розв’язуючи ці задачі, отримаємо значення  pi  ,  qj   і u. Тоді змішані стратегіїотримуються за виразами:
.                (5.37)
Приклад 5.10. Знайти розв’язок гри, що описується матрицею
.
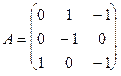Розв’язання. Під час розв’язання цієї гри до кожного елемента матриці А додамо 1 і отримаємо таку матрицю
.
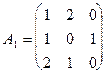Складемо тепер пару взаємодвоїстих задач:
                  
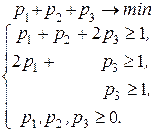
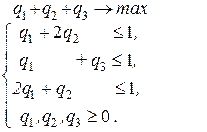
Розв’яжемо другу з них

З оптимальної симплекс-таблиці випливає, що
(q1, q2, q3) = (0; ; 1),
а із співвідношень подвійності випливає, що
( p1, p2, p3) = ( ; 1; 0).
Отже, ціна гри з платіжною матрицею А1 дорівнює
 =,
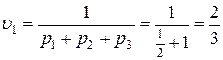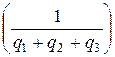а гри з платіжною матрицею А:
.
При цьому оптимальні стратегії гравців мають вигляд:
Х = (х1, х2, х3) = (u р1; u р2; u р3) = = ,
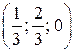Y = (y1, y2, y3) = (u q1; u q2; u q3) = = .

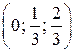5.9 Метод послідовного наближення до ціни гри

Часто під час дослідження операцій виникає ситуація, коли немає потреби в точному розв’язку гри, або через якісь причини не можна знайти точного значення ціни гри та оптимальних змішаних стратегій гравців.
Суть методу полягає в тому, що гра в уяві розігрується кілька разів, тобто в кожній партії гри кожний партнер вибирає ту свою стратегію, яка дає йому найбільший сумарний  виграш. Інакше кажучи, кожний гравець вибирає таку послідовність своїх чистих стратегій, яка забезпечує першому гравцю максимальний середній виграш, а другому - мінімальний середній програш.
Після реалізації кількох партій такої гри обчислюється середнє значення виграшу першого гравця, програшу другого гравця, а їх середнє арифметичне береться за приблизне значення ціни гри. Крім того, цей метод надає можливість визначити наближене значення оптимальних змішаних стратегій обох партнерів.
Розглянемо матричну гру двох гравців з платіжною матрицею

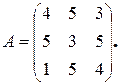
Результати застосування методу зведемо в табл. 5.2:
n1 - найбільший сумарний виграш першого гравця за кілька партій гри, поділений на число партій;
n2 - найменший сумарний програш другого гравця за те саме число партій гри, поділений на число партій
                                     (5.38)
Таблиця 5.2 - Результати застосування методу послідовного наближення до ціни гри

Заповнюємо таблицю таким чином.
Нехай другий гравець вибрав свою першу стратегію, тоді перший виграв:
4, якщо вибере свою першу стратегію;
5, якщо вибере свою другу стратегію;
1, якщо вибере свою третю стратегію.
Ці значення запишемо в 2-5 стовпці табл. 5.2. Максимальний виграш першого гравця буде тоді, якщо він використав свою другу стратегію. При цьому другий гравець програв:
5, якщо вибере свою першу стратегію;
3, якщо вибере свою другу стратегію;
5, якщо вибере свою третю стратегію.
Ці дані запишемо в 6-9 стовпці табл. 5.2. Для другої стратегії першого гравця другий матиме найменший програш, якщо вибере свою другу стратегію. У стовпець 10 запишемо найбільший середній виграш першого гравця, який він має в першій партії гри, тобто 5/1, а у стовпець II занесемо найменший середній програш 3, який мав другий гравець у першій партії, в стовпець 12 запишемо середнє арифметичне, тобто наближене значення  ціни гри: 5/1 + 3/1 : 2 = 8/2. Якщо другий гравець використовуватиме свою другу стратегію у другій партії гри, то перший має отримати 5, 3, 5 відповідно при своїх першій, другій, третій стратегіях, а сумарний виграш його за дві партії гри буде:
4 + 5 = 9 - при його першій стратегії;
5 + 3 = 8 - при його другій стратегії;
1 + 5 = 6 - при його третій стратегії.
Ці сумарні виграші запишемо в другий рядок табл. 5.2 (стовпці 3-5). З них найбільшим є 9, що відповідає першій стратегії першого гравця, тобто в цій партії йому необхідно вибрати цю свою стратегію. Другий гравець програв при цьому 4, 5, 3 відповідно при першій, другій, третій своїх стратегіях, а його сумарний програш за дві партії гри буде:
5 + 4 = 9 - при його першій стратегії;
3 + 5 = 8 - при його другій стратегії;
5 + 3 = 8 - при його третій стратегії.
Ці сумарні програші запишемо в другий рядок табл. 5.2 (стовпці 7-9).
Із цих програшів найменшим є 8, що відповідає другій та третій його стратегіям, тобто в третій партії гри другий гравець може використовувати будь-яку з цих двох стратегій, нехай другу. У стовпці 10 запишемо найбільший сумарний виграш першого гравця за дві партії, поділений на число партій, тобто 9/2, у стовпець 11 - відповідно 8/2 - найменший сумарний програш другого гравця за дві партії, поділений на число партій, а у стовпець 12 - їх середнє арифметичне - 17/4.
Продовжуючи далі цей процес, заповнимо всю табл. 5.2 для 15 партій. Звідси можна обчислити, що наближена змішана стратегія пер­шого гравця має вигляд Х = (5/15, 8/15, 2/15), другого - Y = (4/15, 6/15, 5/I5), а ціна гри - n = 61/15. Точне значення змішаних стратегій гравців буде:

а ціна гри  n = 4,067. Таке наближення буде досить добрим.

5.10 Принцип мінімакса

Розглянуті вище міркування щодо пошуку найкращого плану ігор, зокрема, в умовах конкуренції – не єдиний спосіб розв’язання задач. Часто набагато швидшим і, головне, логічно стрункішим виявляється інший принцип пошуку оптимальних ігрових стратегій за принципом мінімакса. Для ілюстрації цього методу розглянемо попередній приклад гри з трохи видозміненою матрицею, яка зображена у вигляді табл. 5.3.

Таблиця 5.3 – Ігрова матриця

Повторимо міркування, що використані для попереднього прикладу:

• ми ніколи не виберемо стратегію S1, оскільки вона за будь-якої відповіді конкурента принесе нам значні збитки.
• з двох стратегій, що залишилися доцільніше вибрати S3, оскільки за будь-якої відповіді конкурента ми дістанемо прибуток.
• вибираємо як оптимальну стратегію S2.

Міркування нашого конкурента виявляться приблизно такими ж за змістом. Розуміючи, що ми ніколи не приймемо S1 і виберемо, зрештою, S3, він прийме рішення вважати оптимальною для себе стратегію C1 – у цьому випадку він буде мати найменші збитки.
Можна застосувати й інший метод міркувань, що дає, зрештою, той же результат. При виборі найкращого плану гри для нас  можна міркувати так:
- при стратегії S1 мінімальний (min) «виграш» складе – 4000 гривень;
- при стратегії S2 мінімальний (min) «виграш» складе – 1000 гривень;
- при стратегії S3 мінімальний (min) виграш складе + 1000 гривень.
Виходить, що найбільший (max) з найменших (min) виграшів – це 1000 гривень і тому потрібно визначати стратегію S3 оптимальною, з надією на відповідний хід конкурента його стратегією C1. Таку стратегію і називають стратегією MaxMin. Якщо тепер спробувати змоделювати поведінку конкурента, то для нього:
- при стратегії C1 максимальний (max) програш складе 1000 гривень;
- при стратегії C2 максимальний (max) програш складе 2000 гривень.
Виходить, наш конкурент, якщо він буде міркувати тверезо, вибере стратегію C1, оскільки саме вона забезпечує найменший (min) з найбільших (max) програшів. Таку стратегію і називають стратегією MiniMax.
Легко помітити, що це те саме – ви робите хід S3 у розрахунку на відповідь C1, а ваш конкурент – хід C1 у розрахунку на S2.
Тому такі стратегії називають мінімаксними – ми сподіваємося на мінімум максимальних збитків або, що те саме, на максимум мінімального прибутку.
У двох розглянутих прикладах оптимальні стратегії «супротивників» збігалися, прийнято говорити – вони відповідали сідловій точці матриці гри.
Метод мінімакса відрізняється від стандартного шляху логічних міркувань таким важливим показником як алгоритмічність. Справді, можна довести, що якщо сідлова точка існує, то вона знаходиться на перетині деякого рядка S і деякого стовпця C. Якщо число в цій точці найбільше для даного рядка і, одночасно, найменше у даному стовпці, то це і є сідлова точка.
Зазвичай, далеко не всі ігри характеризуються сідловою точкою. Однак якщо вона є, то пошук її для числа рядків і стовпців у кілька десятків, а то і сотень за стандартним логічним планом – справа практично безнадійна без використання комп'ютерних технологій. Але, навіть і при використанні комп'ютера, писати програму для реалізації всіх можливих If ... Then доведеться на спеціальних мовах програмування (наприклад – мова Prolog). Ці мови чудові для розв’язання логічних задач, але практично непридатні для звичайних обчислень.Якщо ж використовувати метод мінімакса, то весь алгоритм пошуку сідлової точки займе мовою Pascal або C++ не більше 5...10 рядків програми.
Розглянемо ще один простий приклад гри, але вже без сідлової точки.
Початкові дані занесено в табл. 5.4.

Таблиця 5.4 – Початкові дані

Задача в цьому випадку для нас (і для нашого розумного конкурента) буде полягати у зміні стратегій, у надії знайти таку їх комбінацію, за якою математичне сподівання виграшу або середній виграш за деяке число ходів буде максимальним.
Нехай ми прийняли рішення половину ходів у грі робити з використанням S1, а іншу половину – з S2. Звичайно, ми не можемо знати, яку зі своїх двох стратегій буде застосовувати конкурент, і тому доведеться розглядати два крайніх випадки його поведінки.
Якщо наш конкурент увесь час буде застосовувати C1, то для нас виграш складе 0,5 (-3000) + 0,5 (+6000) = 1500 гривень.
Якщо ж він увесь час буде застосовувати C2, то наш виграш складе 0,5 (+7000) + 0,5 (+1000) = 4000 гривень.
А це вже привід для міркувань, для аналізу. Зрештою, можна припустити, що ж ми будемо мати у випадку застосування конкурентом також змішаної стратегії? Відповідь уже готова – ми будемо мати виграш не менше 1500 гривень, оскільки виконані вище розрахунки охопили всі варіанти змішаних стратегій конкурента.
Поставимо запитання у більш загальному вигляді – а чи існує найкраща змішана стратегія (комбінація S1 і S2) для нас в умовах застосування змішаних стратегій (комбінації C1 і C2) з боку конкурента? Математична теорія ігор дозволяє відповісти на це запитання точно – оптимальна змішана стратегія завжди існує, але вона може гарантувати мінімум математичного сподівання виграшу. Методи пошуку таких стратегій добре розроблені і наведені в літературі.
Таким чином, ми знову виявилися в ролі ОПР – системний підхід не може дати поради щодо безумовного одержання виграшу. Нам і тільки нам вирішувати – або скористатися рекомендацією і застосувати оптимальну стратегію гри, але при цьому рахуватися з ризиком можливого програшу (виграш виявиться гарантованим лише при дуже великому числі ходів).
Завершимо розгляд останнього прикладу демонстрацією пошуку найкращої змішаної стратегії.
Нехай ми застосовуємо стратегію S1 з частотою e, а стратегію S2 з частотою (1-e). Тоді ми будемо мати виграш
W(C1) = e (-3000) + (1-e)(+6000) = 6000 - 9000e
при застосуванні конкурентом стратегії C1, або будемо мати виграш
W(C2) = e (+7000) + (1-e)(+1000) = 1000 + 6000e
при застосуванні конкурентом стратегії C2.
Теорія ігор дозволяє знайти найкращу стратегію для нас з умови

W(C1) = W(C2),(5.39)

що приводить до найкращого значення e =1/3 і математичному сподіванню виграшу завбільшки (-3000) (1/3) + (+6000) (2/3) = 3000 гривень.

5.11 Моделювання в умовах протидії (моделі торгів)

До цього класу відносяться задачі аналізу систем із протидією (конкуренцією), також ігрових по суті, але з однією особливістю – «правила гри» не постійні в одному єдиному пункті – ціни за те, що продається.
Для невеликого числа учасників торгів цілком придатні описані вище прийоми теорії ігор, але коли число учасників велике і, що ще гірше, заздалегідь невідоме – приходиться використовувати трохи інші методи моделювання ситуацій у торгах. Найчастіше зустрічаються два види торгів:
- закриті торги (auctionsbyatender), у яких два або більше учасники незалежно один від одного пропонують ціни (ставки) за той чи інший об'єкт, при цьому учасник має право лише на одну ставку, а ведучий торги приймає вищу (чи нижчу) із запропонованих;
- відкриті торги (openauctions) або аукціони, коли два або більше учасники підіймають ціни доти, поки надбавка пропонується.
Розглянемо спочатку найпростіший приклад закритих торгів. Нехай ми (A) і наш конкурент (B) беремо участь у закритих торгах двох об'єктів сумарною вартістю C1 + C2.
Ми маємо у своєму розпорядженні вільну суму S і нам відомо, що точно таку ж суму має наш конкурент. При цьому S < C1+C2, тобто купити обидва об'єкти без торгів не вдасться.
Ми повинні призначити свої ціни A1, A2 за перший і другий об'єкти в таємниці від конкурента, який запропонує за них свої ціни B1, B2. Після оголошення цін об'єкт дістанеться тому, хто запропонував найбільшу ціну, а якщо вони збіглися – за жеребом.
Припустимо, що і ми, і наш конкурент володіємо методом вибору найкращої стратегії. Отож – можна довести, що для рівних вільних сум з нашої і з протилежної сторони існує оптимальна для обох сторін стратегія призначення цін. Сутність її (скажемо, для нас) визначається з таких міркувань. Якщо нам вдасться купити перший об'єкт, то наш дохід складе (C1 -A1) або ж, при покупці другого, ми будемо мати прибуток  (C2 - A2). Виходить, у середньому ми можемо очікувати прибуток
d = 0,5(C1 + C2 -A1  -A2) = 0,5(C1+C2-S).               (5.40)
Таким чином, нам найвигідніше призначити ціни
A1 = C1-d = 0,5(C1 - C2 + S);  A2 = C2 - d = 0,5(C2 - C1 + S).           (5.41)
Якщо ж одна з них з розрахунку виявиться негативною – позначимо її нульовою і вкладемо всі гроші в ціну за інший об'єкт.
Але і наш конкурент, маючи ту ж вільну суму і розмірковуючи так само, призначить за об'єкти такі ж ціни. Проте, якщо конкурент не має професійних знань? Що ж, тим гірше для нього – ми будемо мати прибуток більший, ніж конкурент.
Конкретний приклад. Сума вільних грошей складає по 10000 гривень у кожного, ціна першого об'єкта дорівнює 7500, другого 10000 гривень.
Призначимо ціну за перший об'єкт у
0,5(7500-10000+10000) = 3750,
а за другий у             0,5 (10000-7500+10000) = 6250 гривень.
Наш дохід при виграші першого або другого об'єкта складе 3750гривень. Такий же дохід очікує і конкурента, якщо він вибрав таку ж, оптимальну стратегію. Але, якщо він призначив ціну за перший об'єкт 3500, а за другий 6000 гривень (намагаючись заощадити!), то в такому випадку ми можемо виграти торги по двох об'єктах відразу і будемо мати прибуток вже у 7500 гривень – отримуючи майно загальною вартістю в 17500 за ціну у 10000 гривень!
Звичайно, якщо стартові суми учасників торгів неоднакові, число об'єктів велике і велике число учасників, то задача пошуку оптимальної стратегії стає більш складною, але все-таки має аналітичне рішення.
Розглянемо тепер другий вид задачі – відкриті торги (аукціони). Нехай усі ті ж два об'єкти (з тими ж вартостями) продаються з аукціону, у якому беремо участь ми і наш конкурент.
На відміну від першої задачі вільні суми різні і складають SA і SB, причому кожна з них менша (C1+C2) і, крім того, відношення нашої суми до суми конкурента більше 0,5, але менше 2.
Нехай ми знаємо фінансову спроможність конкурента і, оскільки шукаємо оптимальну стратегію для себе, нам байдуже – або знає він те ж про наші фінансові можливості. Задача наша полягає у тому, що ми повинні знати – коли треба припинити підіймати ціну за перший об'єкт. Цю задачу не вирі­шити, якщо ми не визначимо мету своєї участі в аукціоні (системний підхід, нагадаємо, потребує цього). Тут можливі варіанти:
- ми хочемо мати максимальний прибуток;
- ми прагнемо мінімізувати дохід конкурента;
- ми бажаємо максимізувати різницю в доходах – свій побільше, а кон­курента поменше.
Найбільш цікавий третій варіант ситуації – знайти нашу стратегію, що забезпечує
DA -DB = Max.                                        (5.42)
Оскільки об'єктів лише два, то все зважується у процесі торгів за перший об'єкт. Будемо розглядати свій хід у відповідь на чергову пропозицію ціни X за цей об'єкт з боку конкурента.
Ми можемо використовувати дві стратегії двома способами:
- прагнути поступитися першим об'єктом конкуренту – за найбільшу ціну, сподіваючись купити другий;
- прагнути купити перший об'єкт – за мінімальну ціну, поступившись конкуренту другим.
Нехай конкурент призначив за перший об'єкт чергову суму X. Якщо ми не додамо невелику суму (мінімальну надбавку D), то перший об'єкт дістанеться конкуренту. При цьому у конкурента в запасі залишиться сума  SB - X. Дохід конкурента складе при цьому (без врахування D) DB = З1 - X.
Ми напевно купимо другий об'єкт, якщо у нас є SA=(SB - X) + D, тобто не на багато більше, ніж залишилося в конкурента. Виходить, ми будемо мати прибуток DA = C2 -(SB - X) і різниця доходів у цьому випадку складе
DA - DB=C2 - C1 - SB + 2 X.                    (5.43)
Зрозуміло, що ця різниця буде позитивна тільки тоді, коли ми поступимося першим об'єктом за ціну
X > ,                               (5.44)
але ніяк не менше.
Будемо підвищувати ціну за перший об'єкт до суми X+D з метою купити його. Наш дохід складе при цьому DA = C1 - (X + D).
Другий об'єкт дістанеться конкуренту за суму SA - (X + D) + D, оскільки  йому доведеться підняти ціну за цей об'єкт до рівня, трохи більшого від залишку грошей у нас. Дохід конкурента складе DB = C2 - (SA - X + D) + D), а різниця доходів складе (без врахування D)
DA - DB = (C1 - X) - (C2 - SA + X) = С1 - С2 + SA - 2 X.      (5.45)
Ця різниця буде додатна за умови
X <  .                              (5.46)
Ми знайшли дві «контрольні» суми для того, щоб знати – коли треба скористатися однією з двох доступних нам стратегій – вирази (5.44) і (5.46). Середнє цих величин складе
K = +,                         (5.47)
і визначає розумну межу для зміни стратегій нашої участі в аукціоні з метою одночасно отримати дохід собі побільше, а конкуренту – поменше.
Цікаво порахувати свій дохід і різницю доходів на цій межі.
- Якщо ми уступили перший об'єкт на цій межі, то за (5.43)
DA - DB = C2 - C1 - SB + 2 K = 0,5(SA - SB).
- Якщо ж ми купили перший об'єкт на цій межі, то за (5.45)
DA - DB = С1 - С2 + SA - 2 K = 0,5(SA - SB).
Для зручності супроводу числових даних задамо вільні суми і ціни об'єктів (за нашим уявленням про ці об'єкти):
SA = 100 < 175; SB = 110 < 175; C1 = 75; C2 = 100; 0,5 < (SA/SB) < 2
і приймемо дозволену надбавку до ціни, рівною 1.
У цьому конкретному випадку межа «бою» за перший об'єкт проходить через суму (5.47):
K = += - 12,5 + 52,5 = 40 $
Якщо наш конкурент вважає, що об'єкти для нього коштують однаково (він знає нашу вільну суму, а ми знаємо його вільну суму, але іншої інформації ми і він не маємо), то він обчислить цю ж межу і ми будемо задовольнятися різницею доходів не на свою користь:
DA - DB = С1 - С2 + SA - 2 K = 0,5(SA - SB) = -5.
Що ж робити – коли у конкурента більший стартовий капітал. Можливо, що наш конкурент (граючи за себе) буде вважати вартості об'єктів зовсім іншими і для нього границя буде зовсім іншою. Або – мета конкурента у даному аукціоні зовсім не така як наша, що також обумо­вить іншу граничну суму участі в торгах за перший об'єкт. Іншими словами – оптимальна стратегія конкурента нам зовсім невідома. Тоді усе залежить від того, на якій сумі він «віддасть» нам перший об'єкт або навпаки, до якої межі він буде «боротися» за нього. Табл. 5.5 ілюструє цей випадок.
І на завершення питання про відкриті торги – аукціони, відзначимо, що в реальних умовах задача моделювання і вибору оптимальної стратегії поведінки виявляється дуже складною.
Справа не тільки у тому, що число об'єктів може бути набагато більше двох, а що стосується числа учасників, то воно також може бути великим і навіть не завжди відомим заздалегідь. Це призведе до чисто кількісних труднощів під час моделювання «вручну», однак, не відіграє особливої ролі при використанні комп'ютерних програм моделювання. Справа у іншому – здебільшого ситуація ускладнюється невизначеністю, стохастичністю поведінки наших конкурентів. Тому, прийдеться мати справу не із самими величинами (цінами, що замовляються, доходами і т.д.), а з їх математичними сподіваннями, обчисленими за вірогідними моделями, або із середніми значеннями, знайденими за підсумками спостережень статистичних експериментів.

Таблиця 5.5 – Випадок, коли у конкурента більший стартовий капітал

Запитання і завдання для самоконтролю

1. Наведіть класифікацію ігрових ситуацій.
2. Дайте означення термінів матрична та біматрична гра.
3. Що Ви розумієте під поняттям чиста стратегія гри?
4. Що таке сідлова точка? Показати на прикладі.
5. Що таке змішана стратегія гравця?
6. Сформулюйте теорему про мінімакс.
7. Що таке домінування (строге домінування) стратегії одного гравця над стратегією іншого?
8. Наведіть властивості математичних моделей ігрових ситуацій та поясніть їх.
9. Поясніть алгебраїчний метод моделювання ігрових ситуацій на прикладі.
10. Покажіть та поясніть на прикладі графічний метод розв’язання ігор.
11. Який хід виконання операцій у матричному методі моделювання ігрових ситуацій? Наведіть приклад.
12. Опишіть ітеративний метод моделювання ігрових ситуацій.
13. В чому полягає суть методу послідовного наближення до ціни гри?
14. Поясніть на прикладі принцип мінімакса для пошуку оптимальних ігрових стратегій.
15. Поясніть на прикладі моделювання в умовах протидії. Розгляньте випадки закритих та відкритих торгів.

 

---