---

6. МЕТОДИ АНАЛІЗУ ВЕЛИКИХ СИСТЕМ

6.1 Планування експериментів

Ще на початку розгляду питань про цілі і методи системного аналізу ми знайшли ситуації, у яких немає можливості описати елемент системи, підсистему і систему в цілому аналітично, використовуючи системи або рівняння хоча б нерівностей. Іншими словами – ми не завжди можемо побудувати чисто математичну модель на будь-якому рівні – елемента системи, підсистеми або системи у цілому. Такі системи іноді дуже влучно називають «погано організованими» або «слабко структурованими».
Так уже склалося, що протягом майже 200 років після Ньютона у науці вважалося непорушним положення про можливість «чистого» або однофакторного експерименту. Передбачалося, що для з'ясування залежності величини Y=f (X) навіть за умови очевидної залежності Y від багатьох інших змінних завжди можна стабілізувати всі змінні, крім X, і знайти «особистий» вплив X на Y.
Лише порівняно недавно (див. роботи В. В. Налімова) погано організовані або, як їх ще називають – великі системи цілком «законно» стали вважатися особливим середовищем, у якому невідомими є не лише зв'язки всередині системи, але і самі елементарні процеси. Аналіз таких систем (у першу чергу соціальних та економічних) можливий лише при єдиному, науково обґрунтованому підході – визнанні прихованих, невідомих нам причин і законів процесів. Часто такі причини називають латентними факторами, а особливі властивості процесів – латентними ознаками.
Виявилася і вважається також загальновизнаною можливість аналізу таких систем з використанням двох, принципово різних підходів або методів.
Перший з них це метод багатовимірного статистичного аналізу. Цей метод був обґрунтований і застосований відомим англійським статистиком Р. Фішером у 20-30 роках ХХ сторіччя. Подальший розвиток багатовимірної математичної статистики як науки, так і основи багатьох практичних додатків вважається причинно зв'язаним з появою й удосконаленням комп'ютерної техніки. Якщо у 30-і роки, під час ручного оброблення даних вдавалося розв’язувати задачі, в яких існувало 2 ... 3 незалежних змінних, то у 60-і роки розв’язувалися задачі з 6 змінними, а до 70..80 років їх число вже наближалося до 100.
Другий метод, який прийнято називати кібернетичним або «вінерівським»,пов'язуючи його назву з батьком кібернетики Н. Вінером. Коротка сутність цього методу – чисто логічний аналіз процесу керування великими системами. Поява цього методу була цілком природною – оскільки ми визнаємо існування погано організованих систем, то логічним буде порушити питання про пошук методів і засобів керування ними. Зовсім безглуздо порушувати питання про розподіл струмів в електричних колах – ці процеси є добре організованою (законами природи) системою.
Цікаво, що обидва методи, незважаючи на розходження між собою, можуть застосовуватися і з успіхом застосовуються під час системного аналізу одних і тих самих систем.
Так, наприклад, інтелектуальна діяльність людини вивчається «фішерівським» методом – багато психологів, як іронічно зауважує В. В. Налімов, «упевнені, що їм вдасться розібратися в результатах численних тестових іспитів». З іншого боку, побудова так званих систем штучного інтелектує спробою створення комп'ютерних програм, що імітують поведінку людини в області розумової діяльності, тобто застосування «вінерівського» методу.
Очевидно, що економічні системи, швидше за все, слід віднести саме до погано організованих, насамперед тому, що одним з видів елементів у них є людина. А якщо це так, то не дивно, що під час системного аналізу в економіці буде потрібний «реальний» експеримент.
У найпростішому випадку мова може йти про деякий елемент економічної системи, про який нам відомі лише зовнішні впливи (що потрібно для нормального функціонування елементу) і вихідні його реакції (що повинен «робити» цей елемент).
Однією з рятівних ідей, може бути ідея розгляду такого елемента, як «чорний ящик». Використовуючи цю ідею, ми розуміємо, що не в змозі простежити процеси всередині елемента і сподіваємося побудувати його модель без таких знань. Нагадаємо класичний приклад – незнання процесів травлення в організмі людини не заважає нам організовувати своє харчування за «входом» (продукти, які ми споживаємо, режим харчування і т. д.) з врахуванням «вихідних» показників (ваги тіла, самопочуття й інших).
Отже, наші наміри цілком конкретні, а саме «що робити» – ми збираємося подавати на вхід елементу різні зовнішні, керуючі впливи  (controlinfluences) і слідкувати за його реакціями (reactions) на ці впливи.
Тепер треба настільки ж чітко вирішити – а навіщо ми це будемо робити, що ми сподіваємося отримати. Питання це непросте, нечасто можна дозволити собі просто задовольнити свою допитливість.
Як правило, експерименти над реальними системами є вимушеною процедурою, зв'язаною з певними витратами на сам експеримент і, крім того, з ризиком непоправних негативних наслідків.
Теоретичне обґрунтування і методика дій у таких ситуаціях складають предмет особливої галузі науки – теорії планування експерименту.
Визначимо, яку термінологію будемо вживати:
- усе, що подається на вхід елементу, будемо називати керуючими впливами або просто впливами;
- усе, що виходить на виході елементу, будемо називати реакціями;
- якщо ми можемо виділити у системі (підсистемі) декілька однотипних елементів, то їх сукупність будемо називати блоком;
- змістовний опис своїх дій щодо елементів блоку будемо називати планомексперименту.
Дуже важливо зрозуміти мету експерименту, що планується. Зрештою, ми можемо і не отримати ніякої інформації про сутність процесів у ланцюгу «вхід-вихід» у самому елементі. Але якщо ми знайдемо корисність деяких, доступних нам впливів на елемент і переконаємося в надійності отриманих результатів, то досягнемо головної мети експерименту – знаходження оптимальної стратегії керування елементом. Неважко зрозуміти, що поняття «керуючий вплив» дуже широке – від звичайних наказів до під’єднання до елементу джерел енергетичного або інформаційного «живлення». Виявляється, що вже саме складання плану експерименту потребує певних знань і деякої кваліфікації. Досвід доводить доцільність включення в план таких чотирьох компонентів:
- опис множини стратегій керування, серед яких ми сподіваємося вибрати найкращу;
- специфікацію або детальний порівняльний опис елементівблоку;
- правила розміщення стратегій на блоці елементів;
- специфікацію вихідних даних, що дозволяють оцінювати ефективність елементів.
Детальний розгляд компонентів плану експерименту дозволяє помітити, що для його реалізації потрібні знання в різних областях науки, навіть якщо мова йде про економічну систему. Так, під час вибору керуючих впливів не обійтися без мінімальних знань з області технології, дуже часто потрібні знання і в області юридичних законів, екології. Для реалізації третього компонента необхідні знання у області математичної статистики, оскільки потрібно використовувати поняття розподілів випадкових величин, їх математичних сподівань і дисперсій. Також можуть виникнути і ситуації, що вимагають застосування непараметричних методів статистики.
Для того, щоб показати труднощі, що виникають під час складання плану експерименту і навіщо потрібно розуміти методи використання результатів експерименту, розглянемо найпростіший приклад.
Нехай ми виконуємо системний аналіз фірми, що здійснює торгівлю за допомогою мережі «фірмових» магазинів і маємо можливість спостерігати той самий вихідний показник елемента такої системи (наприклад, денний виторг магазину фірми).
Очевидним є намагання знайти спосіб підвищення цього показника, а якщо таких способів виявиться декілька – потрібно вибрати найкращий. Припустимо, що відповідно до першого пункту правил планування експерименту, ми вирішили випробувати чотири стратегії керування магазинами. Коли вже таке рішення прийняте, то нерозумно обмежувати експеримент одним елементом, якщо їх у системі досить багато і ми не маємо впевненості в «еквівалентності» умов роботи всіх магазинів фірми.
Нехай ми маємо N магазинів – досить багато, щоб провести «масовий» експеримент, але їх не можна віднести до одного типу. Наприклад, ми можемо розрізняти чотири типи магазинів: А,Б, В і Г (аптечні, бакалійні, горілчані і галантерейні).
Зрозуміло також і те (хоча для цього потрібно розбиратися в технології торгівлі), що виторг магазина може цілком істотно залежати від дня тижня – нехай робочі дні всіх магазинів: Ср, Пт, Сб, Нд.
Перше, «просте» рішення – вибрати з N кілька магазинів навмання (застосувавши рівновірогідний розподіл їх номерів) і використовувати певний час нову стратегію керування ними. Але такі прості міркування приводять до думки, що це буде не краще рішення. І справді – ми розглядаємо елементи системи як «рівноправні» за декількома показниками:
- ми шукаємо єдину (найкращу) для фірми стратегію керування;
- ми використовуємо єдиний для всіх елементів показник ефективності (денний виторг).
У той же час, ми самі поділили об'єкти на групи і тим самим визнаємо розходження у зовнішніх умовах роботи для різних груп. Мовою ТССА це означає, що професійні знання в області керування торгівлею допомагають нам припустити наявність принаймні двох причин або факторів, від яких може залежати виторг: профіль товарів магазину і день тижня. Ні те, ні інше не може бути стабілізоване – інакше ми будемо шукати щось інше: стратегію керування лише горілчаними магазинами і лише по п'ятницях! А наша задача – пошук стратегії керування усіма магазинами і в усі дні їх роботи.
Хотілося б вирішити цю задачу таким чином: вибирати випадково як групи магазинів, так і дні тижня, але мати гарантію (уже не випадково!)  показності вихідних даних іспитів стратегії.
Теорія планування експерименту пропонує особливий метод рішення цієї проблеми, метод забезпечення або випадковості рандомізації плану експерименту. Цей метод заснований на побудові спеціальної таблиці, що називають латинським квадратом для числа факторів рівному двом.
Для нашого прикладу, з числом стратегій 4, латинський квадрат може мати вигляд однієї з двох наведених нижче табл. 6.1 та 6.2.

     Таблиця 6.1                                          Таблиця 6.2

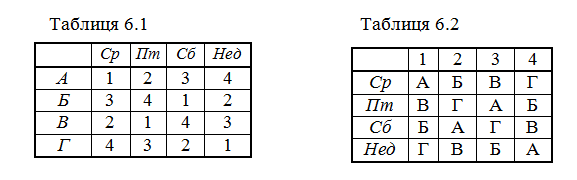
У клітинках табл. 6.1 зазначено номери стратегій для днів тижня і магазинів даного профілю, причому такий план експерименту гарантує перевірку кожної стратегії у кожному профілі торгівлі у кожен день роботи магазину. Звичайно, таких таблиць може бути багато – правила комбінаторики дозволяють знайти повне число латинських квадратів: для «4´4» це число дорівнює 576, для квадрата «3´3» – лише 12, а для «5´5» – 161 280.
У загальному випадку, за наявності t стратегій і двох факторів, що визначають ефективність, буде потрібно N = a× t2 елементів для реалізації плану експерименту, де a у найпростішому випадку дорівнює 1. Це означає, що для нашого прикладу необхідно використовувати 16  «керованих» магазинів, оскільки дані другого рядка і третього стовпця нашого латинського квадрата означають, що по суботах в одному з обраних навмання бакалійних магазинів буде застосовуватися стратегія номер 1.
Відзначимо, що латинський квадрат для нашого прикладу може бути побудований зовсім інакше (табл. 6.2), однак як і раніше буде визначати той же, рандомізований план експерименту.
Нехай ми провели експеримент і отримали його результати у вигляді наведеної нижче табл. 6.3, у клітинках якої зазначені стратегії і результати їх застосування у вигляді сум денного виторгу:

Таблиця 6.3 – Результати експерименту

Якщо обчислити, як і потрібно, середні значення, дисперсії і середньоквадратичні відхилення для четвірок значень денного виторгу (по днях, магазинах і стратегіях), то ми будемо мати такі дані, занесені в табл. 6.4.
Вже таке примітивне статистичне оброблення даних експерименту дозволяє зробити ряд важливих висновків:
- порівняно малі значення розсіювання даних по днях тижня і по категоріях магазинів, що вказує на правильний вибір плану експерименту;
- розкид значень по стратегіях швидше за усе свідчить про більшу залежність денного виторгу від стратегії, ніж від днів тижня або категорії магазину;
- помітна відмінність середнього по 1-й і 3-й стратегіях від середніх по 2-й і 4-й, з цього можна зробити висновок – шукати найкращу стратегію, вибираючи між 1-ою і 3-ою.

Таблиця 6.4 - Результати обробки даних експерименту

У цьому і полягає прямий практичний результат використання рандомізованого плану побудови латинського квадрата.
Але це ще не все. Теорія планування експерименту дає, крім способів побудови планів з урахуванням можливих впливів на величину інших факторів, ще й особливі методи оброблення отриманих експериментальних даних. Сутність цих методів може бути подана таким чином.
Нехай Wis є виторг у i-у магазині при застосуванні до нього s-ї стратегії керування. Будемо розглядати цей виторг як суму складових
Wis = W0 +Ds +ei;                                     (6.1)
де W0 - визначає середній виторг для всіх магазинів за умови застосування до кожного з них всіхстратегій по черзі з дотримання всіх інших умов, що впливають на виторг;
           W0+Ds - є середній виторг при застосуванні до всіх магазинів s-ї стратегії;
ei - розглядається як «помилка виміру» – випадкова величина з нульовим математичним сподіванням і нормальним законом розподілу.
Незважаючи на очевидну нереальність дотримання постійних зовнішніх факторів, що впливають, ми можемо отримати оцінку кожної із складових Wis і шукати оптимальну стратегію через збільшення від її застосування  з урахуванням помилки спостереження. Можна вважати доведеною «нормальність» розподілу величини ei і використовувати «правило трьох сигм» для прийняття рішень за підсумками експерименту.

6.2 Методи аналізу великих систем, факторний аналіз

Вже зрозуміло, що ТССА здебільшого засновує свої практичні методи на основі математичної статистики. Загальновизнано, що в наш час можна виділити три підходи до розв’язання задач, у яких використовуються статистичні дані:
- алгоритмічний підхід, за яким ми маємо статистичні дані про деякий процес і через слабку вивченість процесу ми змушені самі будувати “розумні” правила оброблення даних, базуючись на своїх власних уявленнях про показник, що нас цікавить.
- апроксимаційний підхід, коли ми повністю розуміємо, який існує зв'язок даного показника з наявними у нас даними, але незрозуміла природа виникаючих помилок – відхилень від цих уявлень.
- теоретико-вірогідний підхід, коли потрібно глибоко розуміти суть процесу для з'ясування зв'язку показника із статистичними даними.
В наш час усі ці підходи досить суворо науково обґрунтовані і містять апробовані методи практичних дій. Однак існують ситуації, коли нас цікавить не один, а кілька показників процесу і, крім того, ми підозрюємо наявність декількох впливаючих на процес факторів, які є прихованими, латентними або їх не можна спостерігати.
Найцікавішим і корисним у плані розуміння сутності факторного аналізу – методу розв’язання задач у цих ситуаціях, є приклад використання спостережень експерименту, який проводить природа, ні про яке планування тут не йдеться – ми повинні задовольнятися пасивним експериментом.
Дивно, але й у цих “важких” умовах ТССА пропонує методи виявлення таких факторів, як відсівання слабковиявляючих себе, оцінок значимості отриманих залежностей показників роботи системи від цих факторів.
Нехай ми провели по n спостережень за кожним з k вимірюваних показників ефективності деякої системи і дані цих спостережень подали у вигляді таблиці-матриці 6.5 вхідних даних E[n´k].

Таблиця 6.5 – Матриця вхідних даних Е[n´k]

Нехай ми припускаємо, що на ефективність системи впливають і інші величини (фактори), які не спостерігаються, але їх можна легко інтерпретувати (з'ясувати зміст, причини і механізми впливу). Відразу ж зрозуміємо, що чим більше значення n і чим менше число факторів m (а може їх і немає взагалі), тим більша можливість оцінити їх показник E, що нас цікавить. Настільки ж легко зрозуміти і необхідність умови m < k, з'ясованої на простому прикладі аналогії – якщо ми досліджуємо деякі предмети з використанням усіх 5 людських почуттів, то наївно сподіватися на виявлення більше п'яти “нових” ознак у предметах, які можна легко пояснити, але не можна виміряти, навіть якщо ми “випробуємо” дуже велику їх кількість.
Повернемося до вихідної матриці спостережень E[n×k] і відзначимо, що перед нами, у дійсності, сукупності по n спостережень над кожною з k випадковими величинами E1, E2, … Ek. Саме ці величини “підозрюються” у зв'язках одна з одною – або у взаємній корельованості.
З розглянутого раніше методу оцінок таких зв'язків випливає, що мірою розкиду випадкової величини Ei  є її дисперсія, що обумовлена сумою квадратів усіх зареєстрованих значень цієї величини S(Eij)2 і її середнім значенням (додавання ведеться по стовпцю).
Якщо ми застосуємо заміну змінних у вихідній матриці спостережень, тобто замість Eij будемо використовувати випадкові величини
Xij=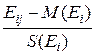,(6.2)
то ми перетворимо вихідну матрицю у нову таблицю-матрицю 6.6 X[n´k].

Таблиця 6.6 – Матриця X[n´k]

Відзначимо, що всі елементи нової матриці X[n´k] є безрозмірними, нормованими величинами і, якщо деяке значення Xij  складе, приміром, +2, то це буде означати тільки одне – у рядку j спостерігається відхилення від середнього по стовпцю i на два середньоквадратичних відхилення (у більшу сторону). Виконаємо тепер такі операції:
- підсумуємо квадрати всіх значень стовпця 1 і розділимо результат на (n-1) – ми одержимо дисперсію (міру розкиду) випадкової величини X1, тобто D1. Повторюючи цю операцію, ми знайдемо так само дисперсії всіх величин, які спостерігаються, але вже є нормованими величинами.
- підсумуємо добуток відповідних рядків (від j = 1 до j = n) для стовпців 1, 2 і також розділимо на (n-1). Те, що ми отримали, називається  коваріацією C12 випадкових величин X1, X2 і служить мірою їх статистичного зв'язку.
- якщо ми повторимо попередню процедуру для всіх пар стовпців, то у результаті отримаємо ще одну квадратну таблицю-матрицю 6.7 C [k´k], яку називають коваріаційною. На її головній діагоналі стоять дисперсії ВВ величин Xi, а інші її елементи – коваріації цих величин (i = 1..k).

Таблиця 6.7 – Коваріаційна матриця

Якщо згадати, що зв'язок ВВ можна описувати не тільки коваріаціями, але й коефіцієнтами кореляції, то у відповідність цій матриці можна поставити матрицю парних коефіцієнтів або кореляційну матрицю R[k´k] (табл. 6.8) з одиничною діагоналлю, а всі її інші елементи – коефіцієнти парної кореляції.

Таблиця 6.8 – Кореляційна матриця

Отже, нехай ми думали, що змінні E, за якими ми спостерігали, є незалежними одна від одної, тобто ми очікували побачити матрицю R [k´k]діагональною, з одиницями на головній діагоналі і нулями в інших місцях. Якщо тепер це не так, то наші здогади про наявність латентних факторів дещо отримали підтвердження.
Але ж як переконатися в правильності наших міркувань, оцінити достовірність нашої гіпотези – про наявність хоча б одного латентного фактора, як оцінити ступінь його впливу на основні (ті що спостерігаються) змінні? А якщо тим більше таких факторів лише декілька – то як їх проранжувати за ступенем впливу?
Відповіді на такі практичні запитання повинен давати факторний аналіз. У його основу покладено метод статистичного моделювання (за висловлюванням В. В. Налімова – модель замість теорії).
Подальший хід аналізу при з'ясуванні таких питань залежить від того, якою з матриць ми будемо користуватися. Якщо матрицею коваріацій C [k´k], то ми маємо справу з методом головних компонентів, якщо ж ми будемо користуватися лише матрицею R [k´k], то ми використовуємо метод факторного аналізу у його звичайному вигляді.
Залишається з’ясувати, що дозволяють обидва ці методи, у чому поля­гає їх відмінність і як ними користуватися. Призначення обох методів однакове – встановити факт наявності латентних змінних (факторів), і якщо вони виявлені, то отримати кількісний опис їх впливу на основні змінні Ei.
Хід міркувань при виконанні пошуку головних компонентів полягає у такому. Ми припускаємо наявність некорельованих змінних Zj (j = 1..k), кожна з яких описана комбінацією основних змінних (додавання по i = 1..k):
Zj = SAji×Xi,                                           (6.3)
і, крім того, має дисперсію, таку що
D(Z1) ³ D(Z2) ³ … ³ D(Zk).                               (6.4)
Пошук коефіцієнтів Aji (їх називають вагою  j-ого компонента в змісті i-ої змінної зводиться до розв’язання матричних рівнянь і не становить особливої складності при використанні комп'ютерних програм. Але сутність цього методу дуже цікава і на ній варто зупинитися.
Як відомо з векторної алгебри, діагональна матриця [2x2] може розглядатися як опис 2-х точок (точніше – вектора) у двовимірному просторі, а така ж матриця розмірністю [k´k]– як опис k точок  k-мірного простору. Отож, заміна реальних, хоча і нормованих змінних Xi на точно таку ж кількість змінних Zj означає не що інше, як поворот k осей багатовимірного простору.
“Перебираючи” по черзі осі, ми знаходимо спочатку ту з них, де дисперсія вздовж осі найбільша. Потім робимо перерахування дисперсій для k-1 осей, що залишилися і знову знаходимо “вісь-чемпіона” по дисперсії і т. д.
Тобто, ми розглядаємо куб (тривимірний простір) по черзі по трьох осях і спочатку шукаємо той напрямок, де бачимо найбільший “туман” (найбільша дисперсія говорить про найбільший вплив чогось стороннього); потім “усереднюємо” картинку по двох осях, що залишилися, і порівнюємо розкид даних по кожній з них – знаходимо “середнячка” і “аутсайдера”. Тепер залишається розв’язати систему рівнянь – у нашому прикладі для 9 змінних, щоб відшукати матрицю коефіцієнтів (ваг) A[k´k].
Якщо коефіцієнти Aji знайдено, то можна повернутися до основних змінних, оскільки доведено, що вони однозначно відображаються у вигляді (додавання по j = 1..k)
Xi=SAji×Zj.                                        (6.5)
Пошук матриці ваг A[k×k] потребує використання коваріаційної матриці і кореляційної матриці. Таким чином, метод головних компонентів відрізняється від усіх інших тим, що дає завжди єдиний розв’язок задачі. Правда, трактування цього розв’язку своєрідне:
– ми розв’язуємо задачу про наявність відповідно стількох факторів, скільки в нас спостерігається змінних, тобто питання про нашу згоду на менше число латентних факторів неможливо поставити;
– у результаті розв’язок, теоретично завжди єдиний, а практично пов'язаний з великими обчислювальними труднощами при різних фізичних розмірностях основних величин. Ми отримаємо відповідь приблизно такого вигляду – фактор такий-то (наприклад, привабливість продавців під час аналізу денного виторгу магазинів) займає третє місце за ступенем впливу на основні змінні.
Ця відповідь обумовлена тим, що дисперсія цього фактора виявилася третьою за величиною серед усіх інших. Більше нічого отримати у цьому випадку неможливо. Інша справа, якшо цей висновок виявився нам корисним або ми його проігноруємо – це наше право вирішувати, як використовувати системний підхід!
Трохи інакше здійснюється дослідження латентних змінних у випадку застосування факторного аналізу. Тут кожна реальна змінна розглядається як лінійна комбінація ряду факторів Fj, але у трохи незвичайній формі
Xi = SBji×Fj + Di ,                                                                              (6.6)
причому додавання виконується по j = 1..m, по кожному фактору.
Тут коефіцієнт Bji  прийнято називати навантаженням на j-й фактор з боку i-ї змінної, а останній доданок у (6.6) розглядається як перешкода – випадкове відхилення для Xi. Число факторів m цілком може бути менше від числа реальних змінних n і ситуації, коли ми хочемо оцінити вплив лише одного фактора (ввічливість продавців), тут цілком допустимі.
Саме поняття “латентний”, схований, є фактором, який не можна виміряти безпосередньо. Звичайно ж, немає приладу і немає еталона ввічливості, освіченості, витривалості і под. Але це не заважає нам самим “виміряти” їх, застосувавши відповідну шкалу для таких ознак, розробивши тести для оцінювання таких властивостей по цій шкалі, і застосувавши ці тести до тих же продавців. Так у чому ж тоді “неспостережність”? А у тому, що в процесі експерименту (обов'язково) масового ми не можемо безупинно порівнювати всі ці ознаки з еталонами і нам потрібно брати попередні, усереднені дані, які отримані зовсім не в “робочих” умовах.
Розглянемо ще й такий приклад. Хто буде сперечатися, що результат спортсмена при стрибках у висоту залежить від фактора – “сила штовхаючої ноги”. Так, цей фактор можна виміряти і в звичайних фізичних одиницях (ньютонах або побутових кілограмах), але коли?! Не під час же стрибка на змаганнях! Однак саме в цей робочий час фіксуються статистичні дані, накопичується матеріал для вихідної матриці.
Трохи складніше пояснити сутність самих процедур факторного аналізу простими елементарними поняттями (на думку деяких фахівців з області факторного аналізу – узагалі неможливо). Тому намагатимемося розібратися в цьому, використовуючи досить складний, але, на щастя, доведений у практичному змісті до повної досконалості, апарат векторної або матричної алгебри.
До того як стане зрозуміло необхідність у такому апараті, розглянемо основну теорему факторного аналізу. Суть її полягає в поданні моделі факторного аналізу (6.6) у матричному вигляді
X[k´1] = B[k´m]´F[m´1]+D[k´1],                              (6.7)
і на наступному доведенні істинності виразу
R[k´k]=B[k´m]´ B*[m´k],                              (6.8)
для “ідеального” випадку, коли нев'язки D дуже малі.
Тут B*[m×k] це транспонована матриця B[k×m].
Труднощі задачі пошуку матриці навантажень на фактори очевидна. Ще у шкільній алгебрі вказується на незліченну множину рішень системи рівнянь, якщо число рівнянь більше числа невідомих. Приблизний підрахунок говорить, що нам потрібно буде знайти km невідомих елементів матриці навантажень, у той час як тільки близько k2/2 відомих коефіцієнтів кореляції. Дещо допомагає доведене у теорії факторного аналізу співвідношення між даним коефіцієнтом парної кореляції (наприклад R12) і набором відповідних навантажень факторів:
R12=B11 ×B21+B12×B22 + … +B1m×B2m .
Таким чином, немає нічого дивного у твердженні, що факторний аналіз (а, виходить, і системний аналіз у сучасних умовах) – більше мистецтво, ніж наука. Тут важливо володіти “навичками” і надзвичайно важливо розуміти як потужність, так і обмежені можливості цього методу.
Є ще одна обставина, яка призводить до труднощів при професійній підготовці в області факторного аналізу. Це необхідність бути професіоналом у “технологічному” плані. Однак, з іншого боку, стати професіоналом високого рівня навряд чи можливо, не маючи хоча б уявлень про можливості аналізу й ефективного керування системами на базі рішень, що знайдені за допомогою факторного аналізу.
Слід відзначити, що не треба спокушатися ненадійними обіцянками популяризаторів факторного аналізу, не слід вірити міфам про його всемогутність й універсальність. Цей метод “на вершині” тільки за одним показником – своєю складністю, як по сутності, так і за складністю практичної реалізації навіть при “повальному” використанні комп'ютерних програм.

Запитання і завдання для самоконтролю

1. Які системи називають «погано організованими» або «слабко структурованими»?
2. Що таке латентний фактор?
3. Які Ви знаєте підходи для аналізу великих систем?
4. В чому суть методу багатовимірного статистичного аналізу?
5. В чому суть кібернетичного методу?
6. Сформулюйте предмет галузі науки – теорії планування експерименту.
7. Що називають впливами та реакціями системи?
8. Що таке планексперименту і які компоненти до нього входять?
9. В чому полягає метод рандомізації плану експерименту?
10. Яким чином формується латинський квадрат?
11. Назвіть три підходи до розв’язання задач, у яких використовуються статистичні дані.
12. Поясніть суть методу факторного аналізу.
13. Що таке коваріаційна матриця?
14. Що таке кореляційна матриця?
15. Поясніть відмінність методу головних компонентів від методу факторного аналізу.
16. Як здійснюється дослідження латентних змінних у випадку застосування факторного аналізу?

 

---