Попередня сторінка          Зміст           Наступна сторінка          Електронні посібники ВНТУ

3.3.3 Подання чисел у формі з плаваючою комою

В цифрових пристроях з плаваючою комою числа подаються в нормальній формі

 

(3.16)

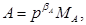
де 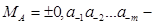мантиса числа А (правильний дріб),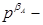характеристика числа А, 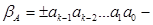порядок (ціле число зі знаком).

Для підвищення точності запису чисел, мантиси в цифрових пристроях з плаваючою комою подаються в нормалізованому вигляді, при якому діапазон подання мантиси лежить в межах:

 

(3.17)

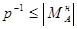
тобто старший розряд мантиси є завжди значущим.

Для запису числа в цифрових пристроях відводиться 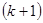 розряд для фіксації порядку зі своїм знаком і  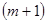розряд для мантиси, тобто місця, що займається в коді числа кодом мантиси і кодом порядку, заздалегідь фіксовані (рис. 3.2).

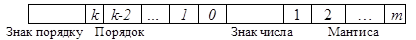
Діапазон подання порядку числа у формі з плаваючою комою лежить в межах 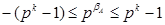. Отже, мінімальне число для р = 2, яке можна подати в елементах пам’яті цифрових пристроїв, визначиться таким чином:.

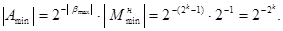
Максимальне число при цьому буде:

,

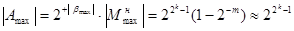(оскільки 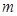 звичайно велике, то  ).

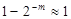Очевидно, що діапазон чисел, що подватись в цифрових пристроях з плаваючою комою, значно більший, ніж в пристроях з фіксованою комою:

 

(3.18)

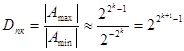
Наприклад, якщо з 32 розрядів 7 + 1 займе порядок числа, а інші 24 ‒ мантиса, то діапазон подання чисел складе:

.

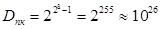Співставляючи між собою розглянуті дві основні форми подання чисел, можна прийти до наступних висновків.

Діапазон подання чисел в цифрових пристроях з фіксованою комою значно менший, ніж в пристроях з плаваючою комою, а точність обчислень залежить від величин початкових чисел. Програмування для цифрових систем з фіксованою комою значно складніше, оскільки доводиться вводити масштабні коефіцієнти, щоб уникнути переповнення розрядної сітки при виконанні арифметичних операцій. При цьому від правильності вибору масштабних коефіцієнтів залежить помилка подання. Отже, їх обчислення повинно проводитися таким чином, щоб виключити можливість появи не тільки переповнення розрядної сітки, але і машинного нуля, що буває часом складно здійснити навіть досвідченому програмісту. Крім того, необхідно пам’ятати, що правильний результат алгебраїчного додавання можливий тільки для однакових масштабних коефіцієнтів, а операції множення і ділення формують нові масштабні коефіцієнти результатів.

Одна цифрові системи з плаваючою комою конструктивно більш складні, оскільки необхідно вводити додаткове обладнання для виконання операцій над порядками чисел, а також передбачити операцію нормалізації і вирівнювання порядків чисел. Плаваюча кома менш зручна, ніж фіксована, і в тих випадках, коли розподіл розрядів в розрядній сітці не відповідає тій схемі, яка заздалегідь прийнята для чисел з плаваючою комою. Найбільш важливий з цих випадків – це операції над командами Крім того, час виконання операцій над числами в цифрових пристроях з плаваючою комою більший, ніж в аналогічних пристроях з фіксованою комою, що зумовлено необхідністю роботи з порядками.

Як і при фіксованій комі, тут можливе переповнення розрядної сітки, яке виражається в тому, що результат якої-небудь операції має порядок, більший допустимого. Це приводить до аварійної ситуації. Привиконанні операцій можливе отримання чисел, що мають порядок, менший допустимого і нормалізовану мантису. Ці числа розглядаються як машинні нулі, так само як і числа, що мають нульову мантису і допустимий порядок.