Отже, емпіричне рівняння регресії в перетворених змінних має вигляд:

. (5.26)

Оцінки коефіцієнтів показової функції рівняння:

, .

Таким чином,

.

Прогнозоване значення на період до 2010 року

.

Як критерій адекватності отриманого рівняння регресії застосовується кореляційне відношення

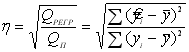, (5.27)

де – сума квадратів відхилень внаслідок показової залежності між у і х.

Для розрахунку кореляційного відношення необхідно побудувати таблицю, аналогічну табл. 5.20.

1.4.2 Моделювання (прогнозування) величини попиту на автоперевезення з урахуванням сезонних коливань

У процесі математичного моделювання економічних явищ і об’єктів часто виникає необхідність оцінювання існуючих коливальних процесів. Під сезонними коливаннями розуміють більш-менш стійку закономірність внутрішньорічної динаміки соціально-економічних явищ. Їхніми причинами є особливості товарної пропозиції, купівельного попиту, зміни витрат залежно від зміни кліматичних умов у різні часові проміжки розглянутого періоду й т.д. Практичне значення вивчення сезонних коливань полягає в тому, що одержувані при аналізі рядів внутрішньорічної динаміки кількісні характеристики відображають специфіку розвитку досліджуваних явищ по місяцях (кварталах) річного циклу.

Сезонні коливання – повторювані з року в рік зміни показника в певні проміжки часу. Спостерігаючи їх протягом декількох років для кожного місяця (або кварталу), можна обчислити відповідні середні або медіани, які приймаються за характеристики сезонних коливань.

Облік сезонних коливань приводить до зниження похибки при розрахунку теоретичних значень показників діяльності організації й при їхньому прогнозуванні. Використання більш точних величин дозволить наблизити розроблювальну модель економічного об’єкта до дійсності, що є однією із завдань при її створенні.

Таким чином, частиною завдання прогнозування повинно бути завдання оцінювання коливальних процесів, які можуть значною мірою впливати на одержувану картину прогнозованого стану об’єкта.

Для прогнозування обсягів перевезень, що мають сезонний характер, використовують такий алгоритм побудови прогнозної моделі.

1. Визначення тренда

Тренд – це зміна, що визначає загальний напрямок розвитку, основну тенденцію часових рядів. Виявлення основної тенденції розвитку (тренда) називається вирівнюванням часового ряду, а методи виявлення основної тенденції – методами вирівнювання.

Першим кроком у побудові моделі є вибір лінії тренда.

Модель прогнозу матиме вигляд:

, (5.28)

де – значення моделі;

– значення лінії тренда;

– значення сезонного компонента;

– величина похибок.

Модель залежить від двох ключових параметрів – та . Параметр визначає довірчий інтервал моделі й дає можливість аналізувати точність побудованої моделі.

Вибір найбільш точної лінії тренда () з високим коефіцієнтом детермінації не є достатньою умовою побудови оптимальної моделі. При рості коефіцієнта детермінації зменшується помилка тренда, але не моделі в цілому.

2. Визначення величин сезонного компонента

Необхідно враховувати також похибки сезонних коливань (), які характеризуються сумою середніх величин сезонного компонента. Чим далі від 0 значення суми коливань сезонного компонента, тим більша помилка параметра .

Таким чином, вибираючи лінію тренда, що характеризує загальну тенденцію розвитку досліджуваного явища, необхідно також розраховувати сезонний компонент () і дивитися на скільки сильно сума середніх значень відхиляється від 0. Якщо ця величина близька до 0, то можна стверджувати, що транспортні перевезення дійсно мають сезонний характер і перевезення можна називати сезонним.

Якщо визначили, що в моделі існує сезонність (сума значень близька до 0), то період сезонності розраховується як середня арифметична між кількістю негативних і позитивних значень сезонного компонента.

     3. Розрахунок помилок моделі

Вивчивши поводження сезонного компонента можна переходити на наступний етап моделювання – розрахунок помилок побудованої моделі.

Похибки розраховуються за формулою:

. (5.29)

Замість значень підставляються фактичні значення об’ємів перевезень. Після знаходження середньоквадратичної похибки моделі ми можемо робити висновок про точність моделі в цілому.

4. Побудова прогнозу

Коли ми визначили найточнішу модель ми можемо перейти на етап прогнозування.

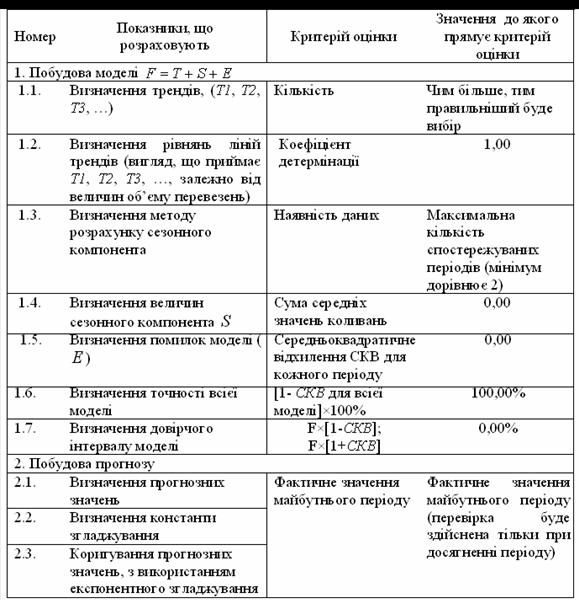
До перерахованих етапів алгоритму розробки моделі прогнозування висуваються критерії, наведені в таблиці 5.24.

Розрахунок

Вихідні дані: обсяги перевезень за шість років. Як вихідну інформацію для прогнозування використаємо інформацію про обсяги перевезень однієї з фірм м. Києва. Дана статистика характеризується тим, що значення обсягів перевезень мають виражений сезонний характер зі зростаючим трендом.

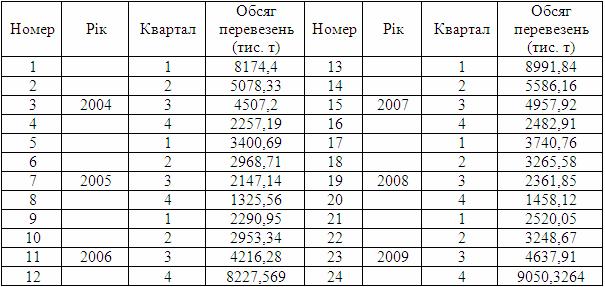
Вихідна інформація подана в табл. 5.25.

Скористаємося алгоритмом, описаним у таблиці 5.24.

Таблиця 5.24 – Алгоритм прогнозування обсягів перевезень

Таблиця 5.25 – Фактичні обсяги перевезень

Створимо моделі, що описують перевезення. Кількість створюваних моделей визначається методом підбору. При цьому варто враховувати, що більша кількість побудованих моделей дасть можливість вибрати найточнішу модель, що описує перевезення.

На початку нам невідомо, яке з рівнянь трендів дасть найкращий результат, тому на даному етапі моделювання доцільніше всього використати всі лінії тренда, які може будувати програмний продукт MS Excel:

– лінійний тренд;

– логарифмічний тренд;

– поліноміальний тренд (візьмемо 6-у степінь, щоб побачити похибки, допущені раніше);

– степеневий тренд;

– експонентний тренд.

Для простоти й більшої наочності даного приклада, а також відбиття суті запропонованого алгоритму обмежимося вибором трьох ліній тренда: поліноміальний, лінійний і логарифмічний тренд.

За коефіцієнтами детермінації видно, що найточнішим є поліном, а найменш точним – лінійний тренд. Але тому що коефіцієнт детермінації () не визначає точність всієї моделі, то вибір тренда на цьому етапі ми завершити не можемо.

Рівняння ліній тренда приймають вигляд, зазначений на рисунку 5.1. Щоб одержати цифрові значення ліній тренда за кожний квартал, необхідно внести рівняння, показані на графіку в середовище MS Excel у вигляді формул, де (незалежний компонент) – це послідовність чисел від 1 до 24, а – значення рівняння лінії тренда для кожного з .

Аналогічно поліному, розрахуємо лінійний і логарифмічний тренди.

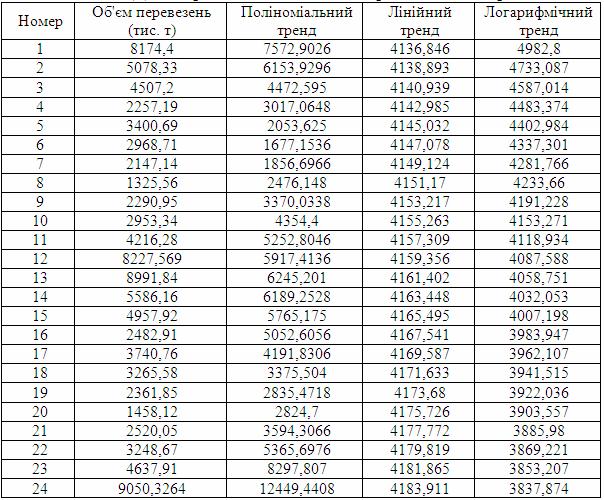
Результати розрахунків наведено в таблиці 5.26.

Використовуючи методику, розраховуємо сезонний компонент для кожного з рівнянь тренда. З фактичних даних віднімаємо значення ліній тренда для кожного із сезонів.

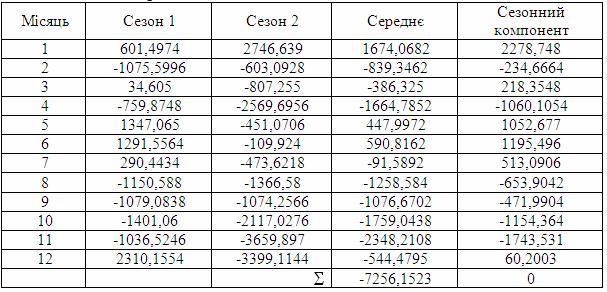
У таблиці 5.27 чітко видно, що відхилення сезонних коливань моделі з поліноміальним трендом від 0 досить велике й стверджувати, що в моделі виявлена сезонність, ми не можемо. Якщо припустити, що сезонність існує, виходячи з економічних міркувань і знань специфіки ринку й перевезень, то помилка моделі в підсумку виросте. Таким чином, висока точність моделі, отримана завдяки вибору полінома, буде нейтралізована низькою точністю сезонного компонента. Щоб перевірити дане твердження, побудуємо повністю модель із поліноміальним трендом.

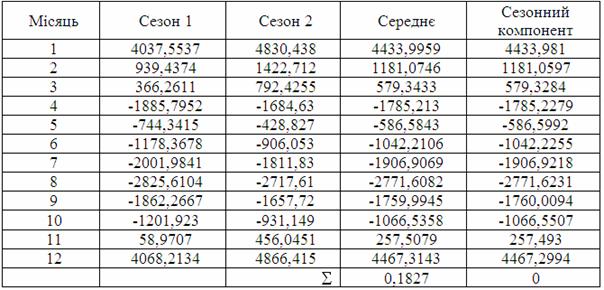
З таблиці 5.28 з суми середніх величин видно, що спостерігається сезонність коливань, тому що сума середніх величин сезонних коливань близька до 0.

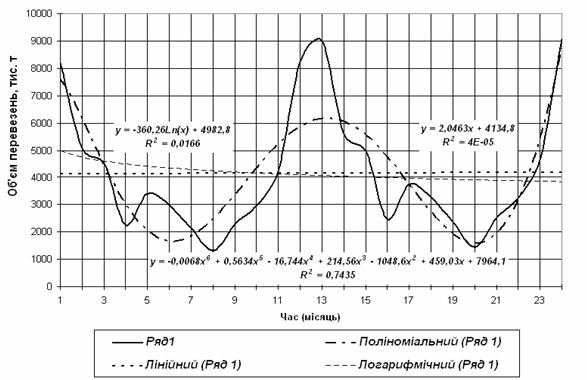
Рисунок 5.1 – Обрані лінії тренда

Таблиця 5.26 – Дані отримані за допомогою рівнянь ліній трендів

Таблиця 5.27 – Розрахунок сезонного компонента для моделі з поліноміальним трендом

Таблиця 5.28 – Розрахунок сезонного компонента для моделі з лінійним трендом

Щоб довести середні коливання до 0, необхідно підсумкову суму середніх розділити на кількість періодів у сезоні (у нашому випадку – це 12). Отриманий результат віднімаємо від значень середнього по кожному періоду. У підсумку – сума коливань складе абсолютний 0.

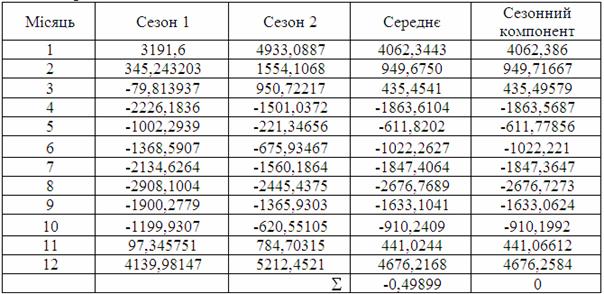
За даними таблиці 5.29 можна стверджувати, що в моделі з логарифмічним трендом також існують сезонні коливання, тому що сума середніх близька до 0.

Розраховані сезонні компоненти для кожного з рівнянь тренда при прогнозуванні просто переносяться на відповідні місяці прогнозного періоду.

Таблиця 5.29 – Розрахунок сезонного компонента для моделі з логариф-мічним трендом

Одержавши три сезонні компоненти () з трьох рівнянь тренда (), ми можемо розрахувати похибки побудованих моделей (). Для цього із значень вихідних даних, необхідно відняти суму , .

Дані розрахунку заносимо в таблицю 5.30.

Таблиця 5.30 – Значення моделей () і їхніх помилок ()

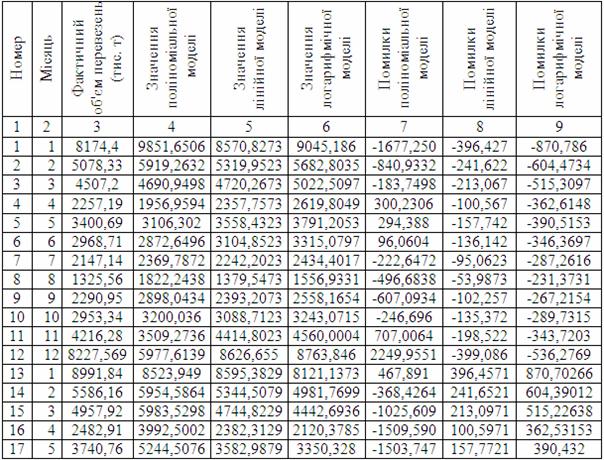
На підставі розрахованих помилок () розрахуємо середньоквадратичне відхилення (СКВ) для кожного з періодів (таблиця 5.31) за формулою:

, (5.30)

де – трендове значення обсягів перевезень;

– сезонна компонента;

– відхилення моделі від фактичних значень.

Таблиця 5.31 – Середньоквадратичне відхилення значень моделі від фактичних даних

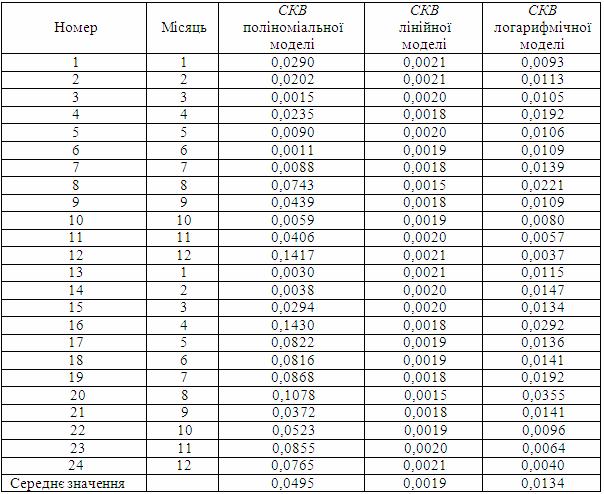
В таблиці 5.31 наведені параметри середньоквадратичних відхилень значень моделі від фактичних даних.

5. Розрахунок точності

Розрахувавши середнє значення СКВ, отриманих для кожної моделі, розрахуємо точність за формулою:

Точність моделі = [1 – (середнє значення СКВ)]?100%.

Точність моделі з поліноміальним трендом дорівнює 95,05% .
Точність моделі з лінійним трендом дорівнює 99,81%.
Точність моделі з логарифмічним трендом дорівнює 98,66%.

Таким чином, високу точність мають всі 3 моделі (рисунок 5.2).

У випадку, коли точність моделі коливається в районі 90-100%, можна стверджувати, що модель досить точна. Однак модель із лінійним трендом є найточнішою, тому що її показник точності найвищий.

Отже, прогноз, зроблений на підставі даних лінійної моделі буде найточнішим.

В подальших розрахунках використовуємо модель із лінійним трендом через її найбільшу точність.

Щоб побудувати довірчий інтервал скористаємося даними СКВ для моделі з лінійним трендом (СКВ = 0,0019). Довірчий інтервал прийме вигляд:

(5.31)

Дані розрахунку зведемо в таблицю 5.32.

6. Побудова прогнозу

Визначивши найточнішу модель, можемо побудувати прогноз змін перевезень на 2010 рік.

Умови прогнозування

Для розрахунку прогнозних значень у пакеті MS Excel, вкажемо умови прогнозування:

– трендова компонента () залежить від послідовності чисел від 1 до 24. Отже, щоб побудувати прогноз, необхідно продовжити цю послідовність до 36. Значення трендової компоненти MS Excel розрахує в автоматичному режимі. Досить виділити останню комірку 24-го номера й затиснувши чорний квадратик у нижньому правому куті комірки протягти виділення до 36 періоду. У підсумку одержимо трендову компоненту ;

– сезонна компонента () розрахована для моделі, залишається незмінною для 25-36 номера. Виділимо в MS Excel сезонну компоненту і скопіюємо на періоди 25-36;

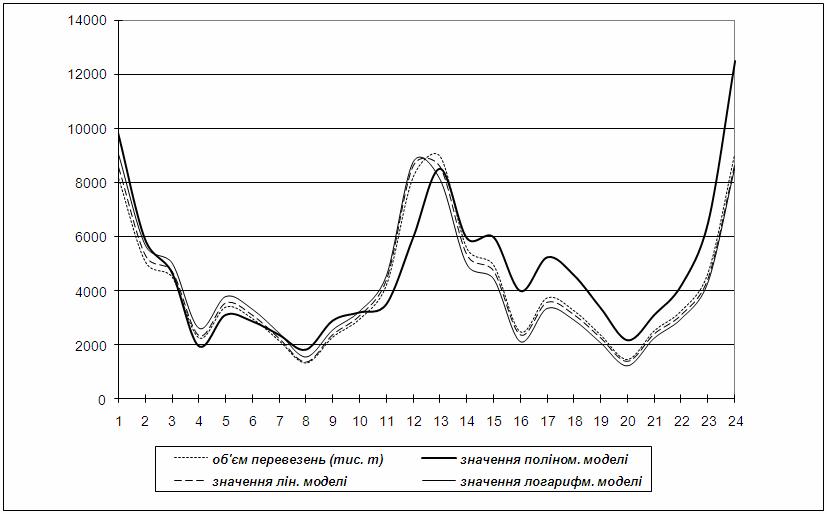
Рисунок 5.2 – Моделі, побудовані на підставі різних ліній тренда