5.3 Приклад виконання завдання

 

Приклад 1. Точка рухається в площині xОy за законом:

 

x=5t² (м),

y=2t (м).

 

Знайти: y=f(x), V₁, a₁, ρ₁ при t₁=0,5c.

 

Розв’язання

Нехай закон руху точки описаний рівняннями:

x=5t² (м),

y=2t (м).

 

Тоді: ,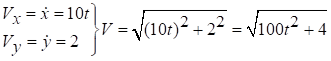

;.

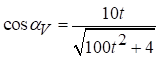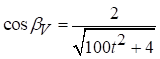Нехай t=0,5 c:

Нехай :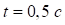

а) , ,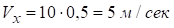

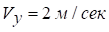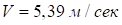
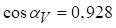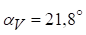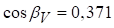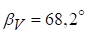; ; ; , (рис. 5.2, а);

б) 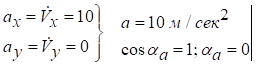 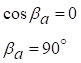(                                 а)                                                            б)

Рисунок 5.2, б),

,

,

 

.

 

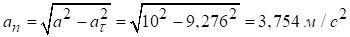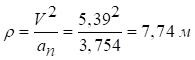Траєкторію можна побудувати графічно по точках, змінюючи час t за якимось кроком, і обчислюючи для кожного t координати х і у точок, що належать траєкторії.

Більш зручно, виключаючи параметр t, отримати рівняння траєкторії у формі: y=f(x), чи x=f(y). У нашому прикладі t=y/2, звідси 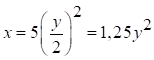 ‑ рівняння параболи (рис. 5.2).

 

                                 а)                                                            б)

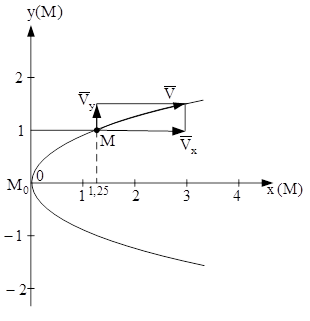
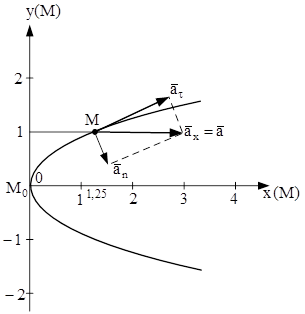
Рисунок 5.2 

 

Розмітка траєкторії полягає у встановленні початку відліку. Масштаб і додатній напрямок можуть обиратися довільно. Звичайно рух точки починається у деякий заданий момент часу t₀ (частіш за все відсутність будь-яких додаткових міркувань покладає t₀=0).

Можливі й відмінні від нуля значення t₀. Тоді при t₀ визначають положення точки M₀ з координатами x₀=x(t₀) і y₀=y(t₀) ‑ рух матеріальної точки тепер починається з початку відліку.

У розглянутому прикладі:  x₀=0,  y₀=0 (точка рухається по верхній вітці параболи).

Якщо точка рухається вздовж траєкторії в постійному напрямку, то природно цей напрямок вважати додатним. Масштаб уздовж траєкторії можна обрати таким же, що і уздовж вихідних координатних осей Ох і Оу.

Відповідь: x=1,25t², V₁=5,39 м/с , a₁=10 м/с², ρ₁=7,74 м.

 

Приклад 2. Точка рухається в площині xОy за законом:

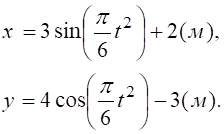
Знайти: y=f(x), V₁, a₁, ρ₁ при t₁=1c.

 

Розв’язання

Параметричні рівняння руху 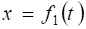  та 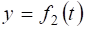 запишемо у вигляді:

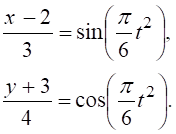
Враховуючи, що 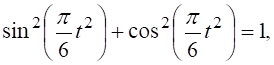 з рівнянь руху отримаємо траєкторію руху точки в координатній формі:

.

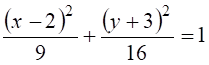Будуємо траєкторію руху точки і знаходимо положення точки на траєкторії при  t₁=1с (рис. 5.3).

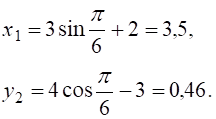
Знаходимо швидкість точки.

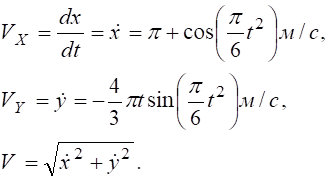
при t₁=1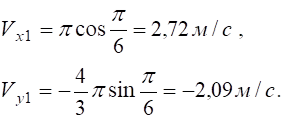  

 

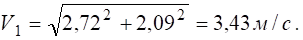
Показуємо V_x1, V_y2, V₁ (рис. 5.3) у вибраному масштабі швидкостей  μ_V=1см : 1 м/с.

Визначаємо прискорення точки

при t₁=1c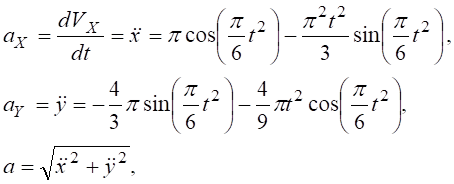  

 

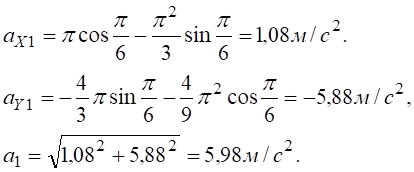
У масштабі прискорень μ_а=1см : 1 м/с² показуємо a_x1, a_y2, a₁ (рис. 5.3).

Радіус кривизни траєкторії точки при t₁=1c

,

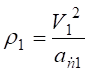де 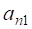- проекція прискорення точки на нормальну вісь

 

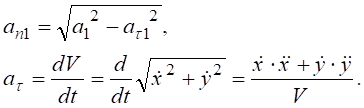
при t₁=1c             

 

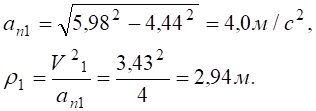
Відповідь: 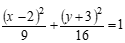, V₁=3,43 м/с , a₁=5,98 м/с², ρ₁=2,94 м.