7 ПЛОСКОПАРАЛЕЛЬНИЙ (ПЛОСКИЙ) РУХ ТІЛА

7.1 Теоретичні відомості і методичні вказівки

Рух твердого тіла у просторі називають плоскопаралельним (плоским), якщо всі точки тіла рухаються у площинах, паралельних деякій нерухомій площині (площина ковзання).

7.1.1 Швидкості точок плоскої фігури

Швидкість будь-якої точки В плоскої фігури складається зі швидкості полюса А і швидкості точки В при обертанні плоскої фігури навколо полюса А, яка перпендикулярна до АВ.

; .

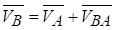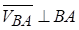Швидкість 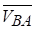 за величиною дорівнює

,

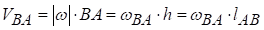де ω - алгебраїчна кутова швидкість плоскої фігури, що не залежить від вибору полюса.

Вектор 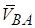 спрямований перпендикулярно до АВ проти напрямку годинникової стрілки навколо полюса А, якщо ω>0, і навпаки, якщо ω<0.

Теорема про проекції швидкостей двох точок тіла на вісь, що проходить через ці точки.

Рисунок 7.1 

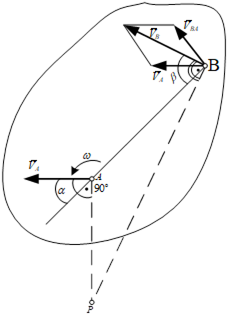
Проекції швидкостей двох точок фігури на вісь, що проходить через ці точки, дорівнюють одна одній (рис. 7.1).

Проекція 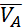 на вісь АВ дорівнює проекції  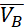на вісь АВ, тобто

,

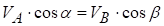де α і β ‑ кути між 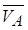 і 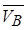 і напрямком осі АВ відповідно.

За теоремою Ейлера-Шаля плоский рух вважається як обертальний  навколо миттєвого центра обертань, або центра швидкостей.

Полюсом є миттєвий центр швидкостей (МЦШ), тобто така точка Р рухомої площини, жорстко скріпленої з фігурою, швидкість якої в певний момент часу дорівнює нулю .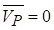

Тоді 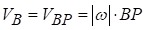, тобто швидкість будь-якої точки фігури дорівнює за величиною добутку модуля кутової швидкості фігури на відстань від цієї точки до МЦШ та спрямована перпендикулярно до цього відрізку  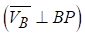проти напрямку годинникової стрілки, якщо ω>0 і навпаки.