7.1.2 Прискорення точок плоскої фігури

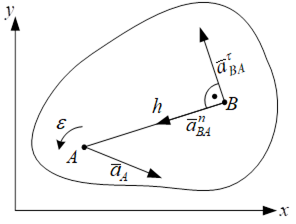
Прискорення будь-якої точки плоскої фігури геометрично складається з прискорення полюса і прискорення точки в обертальному русі тіла навколо полюса, що складається з доцентрового (нормального) і обертального (тангенціального) прискорень (Рисунок 7.2).

Рисунок 7.2 

, , ,

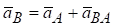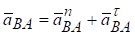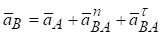де 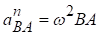 ‑ спрямовано уздовж АВ від точки В до точки А;  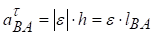‑ завжди спрямоване перпендикулярно до АВ, що з’єднує точку В з полюсом А (рис. 7.3), у бік кутового прискорення ε.

.

Рисунок 7.3 

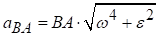Таким чином, прискорення 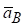 будь-якої точки В плоскої фігури може бути знайдено як геометрична сума трьох прискорень: прискорення полюса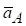, доцентрового прискорення  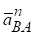і обертального прискорення  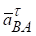точки В навколо полюса А. Вектор  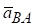має напрямок під кутом α до прямої ВА. При цьому

; .

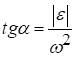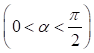Питання для самоперевірки знань

та контролю засвоєння матеріалу

1. Який рух твердого тіла називають плоскопаралельним або плоским?
2. Як визначається швидкість будь-якої точки плоскої фігури?
3. Яку точку плоскої фігури називають миттєвим центром швидкості?
4. Як знаходиться миттєвий центр швидкостей тіла при плоскому русі?
5. Як визначається прискорення будь-якої точки плоскої фігури?
6. Як визначається кутова швидкість ланки плоскої фігури?
7. Як визначається кутове прискорення  плоскої фігури